(i) 2x + 3y = 7; 3x + 5y = 9

(ii) 5x + 3y = 17; 3x + 7 y = 31

(iii) 2x + y − z = 3, x + y + z = 1, x − 2 y − 3z = 4

(iv) x + y + z = 6, 2x + 3y − z = 5, 6x − 2 y − 3z = − 7

(v) x + 4 y + 3z = 2, 2x − 6 y + 6z = −3, 5x − 2 y + 3z = −5

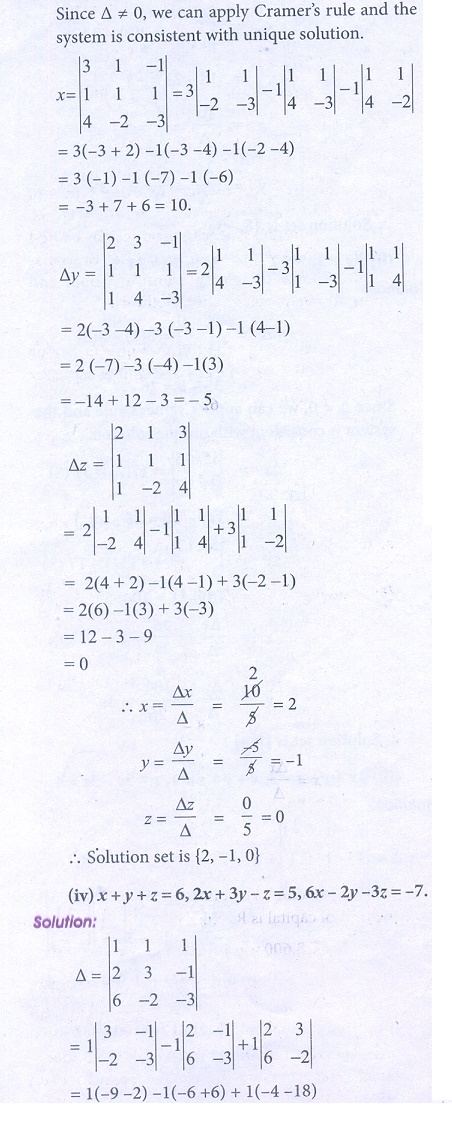
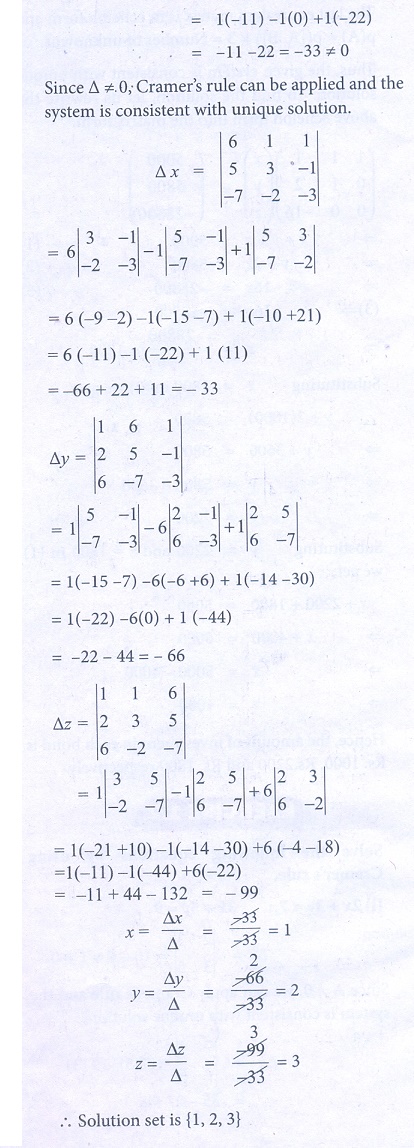
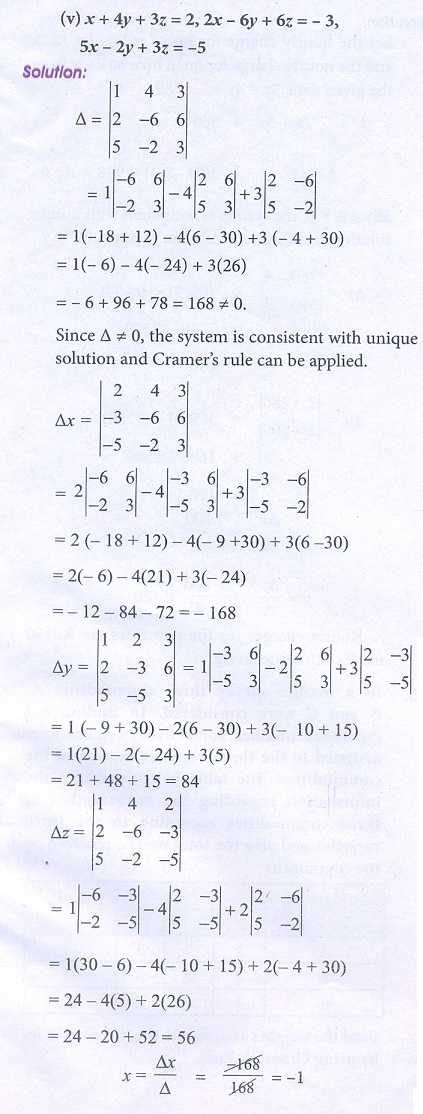
یعنی A = [ a ij ] n×n یک ماتریس متقارن است، سپس a ij = a ji برای همه i و j است .

به عنوان مثال، 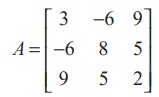یک ماتریس متقارن است زیرا A' =A.

به عنوان مثال، A =

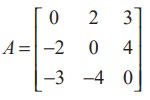
یک ماتریس متقارن کج است زیرا A T = - A است

قضیه 7.1: هر ماتریس مربعی را می توان به صورت مجموع ماتریس های متقارن و ماتریس های متقارن کج نوشت.

برای هر ماتریس مربعی A با ورودی های اعداد حقیقی ، A '+ A یک ماتریس متقارن و A '- A یک ماتریس متقارن چوله است.

Proof

Let B = A + A'.

B' = ( A + A' )' = A' + ( A' )' = A'+ A = A + A' = B .

B ماتریس های متقارن است

C = A − A'

C ' = ( A + ( − A' ))' = A' + ( − A' )' = A' − ( A' )' = A' − A = − ( A − A' ) = − C

C ماتریس های متقارن کج است

و داریم

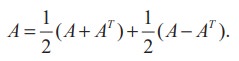
مثال

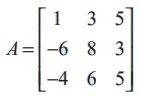
Solution

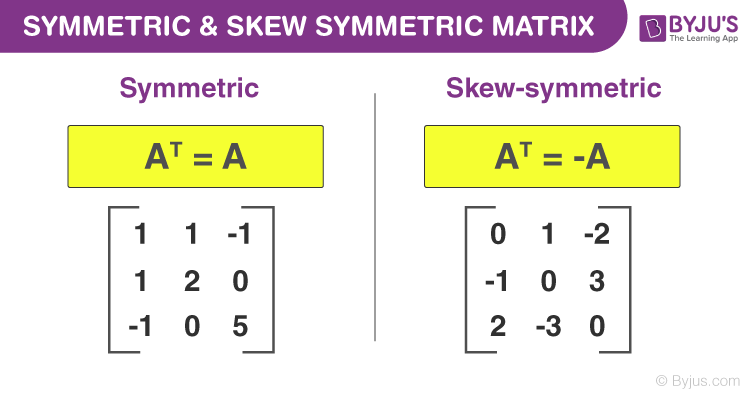
یک ماتریس متقارن و یک ماتریس متقارن کج هر دو ماتریس های مربعی هستند. اما تفاوت بین آنها این است که ماتریس متقارن برابر با ترانهاده آن است در حالی که ماتریس متقارن کج ماتریسی است که ترانهاده آن برابر با منفی آن است.

اگر A یک ماتریس متقارن است، A = A^ T و اگر A یک ماتریس متقارن کج باشد، A^ T = – A است.

​

همچنین بخوانید:

• ماتریس مثلثی بالایی
• ماتریس قطری
• ماتریس همانی

ماتریس متقارن

برای درک اینکه آیا یک ماتریس یک ماتریس متقارن است، بسیار مهم است که در مورد ترانهاده یک ماتریس و نحوه پیدا کردن آن اطلاعات داشته باشید. اگر سطرها و ستون های یک ماتریس m×n را با هم عوض کنیم تا یک ماتریس n×m بدست آوریم، ماتریس جدید را ترانهاده ماتریس داده شده می نامند . دو احتمال برای تعداد سطر(m) و ستون (n) یک ماتریس وجود دارد:

• اگر m = n، ماتریس مربع است
• اگر m ≠ n، ماتریس مستطیل شکل است

در مورد دوم، ترانهاده یک ماتریس هرگز نمی‌تواند با آن برابر باشد. این به این دلیل است که برای برابری، ترتیب ماتریس ها باید یکسان باشد. از این رو، تنها موردی که ترانهاده یک ماتریس می تواند برابر با آن باشد، زمانی است که ماتریس مربع باشد. اما این تنها شرط اول است. حتی اگر ماتریس مربع باشد، ترانهاده آن ممکن است با آن برابر باشد یا نباشد.

در اینجا، می توانیم ببینیم که A ≠ A'.

می بینیم که B = B'. هر زمان که این اتفاق برای هر ماتریسی بیفتد، یعنی زمانی که ترانهاده یک ماتریس با آن برابر باشد، ماتریس به عنوان ماتریس متقارن شناخته می‌شود . اما چگونه می‌توانیم بدون یافتن جابه‌جایی آن متوجه شویم که آیا یک ماتریس متقارن است یا نه؟ ما آن را میدانیم:

بنابراین، اگر برای یک ماتریس A، a ij = a ji (برای همه مقادیر i و j) و m = n باشد، پس ترانهاده آن با خودش برابر است. بنابراین یک ماتریس متقارن همیشه مربع خواهد بود.

تمرین :چند نمونه از ماتریس های متقارن مثال بزنید

ویژگی های ماتریس متقارن

• جمع و تفاضل دو ماتریس متقارن منجر به ماتریس متقارن می شود.
• اگر A و B دو ماتریس متقارن باشند و از خاصیت جابجایی یعنی AB =BA پیروی کنند، حاصل ضرب A و B متقارن است.
• اگر ماتریس A متقارن است، A ^n نیز متقارن است، جایی که n یک عدد صحیح است.
• اگر A یک ماتریس متقارن است، A ^-1 نیز متقارن است.

ماتریس متقارن کج

یک ماتریس فقط در صورتی می تواند متقارن باشد که مربع باشد. اگر ترانهاده یک ماتریس برابر با منفی خودش باشد، ماتریس را متقارن کج می گویند . این بدان معنی است که برای اینکه یک ماتریس متقارن باشد،

A'=-A

همچنین، برای ماتریس، ji =-a ij (برای همه مقادیر i و j). عناصر قطری یک ماتریس متقارن اریب برابر با صفر است. این را می توان از طریق زیر ثابت کرد:

عناصر قطری با فرمول کلی مشخص می شوند.

a ij ، جایی که i = j

اگر i = j، آنگاه a ij = a ii = a jj

اگر A متقارن کج باشد، پس

⇒ a ii = – a ii

⇒ a ii = 0

بنابراین، a ij = 0، زمانی که i = j (برای همه مقادیر i و j)

تمرین :چند نمونه از ماتریس های متقارن کج مثال بزنید

ویژگی های ماتریس متقارن کج

• وقتی دو ماتریس متقارن کج را اضافه می کنیم، ماتریس حاصل نیز کج متقارن است.
• حاصل ضرب اسکالر ماتریس متقارن کج نیز یک ماتریس کج متقارن است.
• قطر ماتریس متقارن اریب از عناصر صفر تشکیل شده است و بنابراین مجموع عناصر در قطرهای اصلی برابر با صفر است.
• هنگامی که ماتریس همانی به ماتریس متقارن اریب اضافه می شود، ماتریس حاصل معکوس است.
• تعیین کننده ماتریس متقارن کج غیر منفی است

تعیین کننده ماتریس متقارن کج

اگر A یک ماتریس اریب متقارن است، که آن هم یک ماتریس مربع است، دترمیتان A باید شرط زیر را برآورده کند:

Det (A^ T ) = det (-A) = (-1)^ n det (A)

معکوس ماتریس متقارن کج وجود ندارد زیرا دترمیتان آن که مرتبه فرد داشته باشد صفر است و بنابراین منفرد است.

مقدار ویژه ماتریس متقارن کج

اگر A یک ماتریس کج متقارن حقیقی باشد، مقدار ویژه آن برابر با صفر خواهد بود. از طرف دیگر، می توان گفت، مقادیر ویژه غیرصفر A غیر حقیقی هستند.

هر ماتریس مربع را می توان به صورت مجموع یک ماتریس متقارن و یک ماتریس متقارن کج بیان کرد.

درس تصویری

75,131

سوالات متداول - سوالات متداول

ماتریس متقارن چیست؟

ماتریس متقارن یک ماتریس مربع است که برابر با ترانهاده خودش است. اگر A یک ماتریس متقارن است، پس شرط را برآورده می کند: A = A T

چگونه متوجه می شوید که یک ماتریس متقارن است؟

برای اینکه بفهمید یک ماتریس متقارن است، ترانهاده آن ماتریس را پیدا کنید. اگر ترانهاده آن ماتریس با خودش برابر باشد، یک ماتریس متقارن است.

مثالی از ماتریسی بزنید که متقارن است اما معکوس پذیر نیست.

ماتریس صفر (مربع) یکی از این ماتریس ها است که به وضوح متقارن است اما معکوس پذیر نیست.

آیا ماتریس متقارن قطری است؟

بله، یک ماتریس متقارن همیشه قابل قطری است.

ماتریس کج متقارن چیست؟

ماتریس کج متقارن ماتریس مربعی است که ترانهاده آن برابر با منفی آن است. باید شرایط زیر را برآورده کند:
A^ T = – A
اگر aij مقدار ردیف i و ستون j را نشان می‌دهد، آنگاه شرط ماتریس متقارن کج به‌دست می‌آید.
a ij = -a ji

تفاوت بین ماتریس متقارن و متقارن کج چیست؟

ترانهاده ماتریس متقارن برابر با همان ماتریس است.

​

1. مثالی از ماتریس پایین مثلثی 2 در 2 بزنید
2. ثابت کنید ماتریس پایین مثلثی 2 در 2 با درایه های قطری غیر صفر معکوس پذیر است
3. ثابت کنید ماتریس پایین مثلثی 3 در 3 با درایه های قطری غیر صفر معکوس پذیر است
4. مثالی از ماتریس بالا مثلثی 2 در 2 بزنید
5. ثابت کنید ماتریس بالا مثلثی 2 در 2 با درایه های قطری غیر صفر معکوس پذیر است
6. ثابت کنید ماتریس بالا مثلثی 3 در 3 با درایه های قطری غیر صفر معکوس پذیر است

1. با مثال نشان دهید ضرب دو ماتریس پایین مثلثی 3در 3 ، پایین مثلثی 3در 3 است
2. با مثال نشان دهید ضرب دو ماتریس پایین مثلثی 4در 4 ، پایین مثلثی 4در 4 است
3. با مثال نشان دهید ضرب دو ماتریس بالا مثلثی 3در 3 ، بالا مثلثی 3در 3 است
4. با مثال نشان دهید ضرب دو ماتریس بالا مثلثی 4در 4 ، بالا مثلثی 4در 4 است
5. ثابت کنید ضرب دو ماتریس پایین مثلثی 3در 3 ، پایین مثلثی 3در 3 است
6. ثابت کنید ضرب دو ماتریس پایین مثلثی 4در 4 ، پایین مثلثی 4در 4 است

ماتریس قطری چیست؟

ما کاربردها و خواص ماتریس قطری ، ماتریس مثلث بالا و ماتریس مثلث پایین را معرفی و مورد بحث قرار می دهیم.

ماتریس قطری یک ماتریس مربع است که در آن همه ورودی‌ها صفر هستند، به جز مواردی که در قطراصلی قرار دارند. به آن ماتریس مقیاس‌بندی نیز می‌گویند زیرا ضرب با ماتریس قطریک شی را در فضای برداری مربوطه مقیاس می‌دهد.

یک ماتریس قطرهمچنین دارای خواص یک ماتریس مثلثی بالا و یک ماتریس مثلثی پایینی است.

ماتریس مثلثی بالایی

یک ماتریس مثلثی بالایی از ورودی های صفر زیر قطر اصلی تشکیل شده است.

یک ماتریس مثلثی بالایی لزوماً یک ماتریس قطری نیست. ماتریس زیر مثلثی بالایی است، اما قطری نیست.

ماتریس مثلثی پایینی

در یک ماتریس قطری پایین، فقط ورودی های بالای قطر اصلی باید صفر باشند.

یک ماتریس مثلثی پایین نیز لزوماً یک ماتریس قطری نیست.

کاربرد ماتریس های قطری و مثلثی چیست؟

اگر ورودی های زیر قطرصفر باشند، ماتریس به شکل ردیف ردیف است . این بدان معناست که سیستم خطی تعریف شده توسط ماتریس به راحتی از طریق جایگزینی قابل حل است. حذف گاوس جردن ضروری نیست.

توجه داشته باشید که به راحتی می توانید یک ماتریس مثلثی بالا را با مرتب کردن مجدد سطرها به شکل ردیفی تبدیل کنید.

جبرهای ماتریس های مثلثی

مثلث بالایی با بسیاری از عملیات حفظ می شود:

• مجموع دو ماتریس مثلث بالایی مثلث بالایی است.
• حاصل ضرب دو ماتریس مثلث بالایی مثلث بالایی است.
• معکوس یک ماتریس مثلث بالایی، اگر وجود داشته باشد، مثلث بالایی است.
• حاصل ضرب یک ماتریس مثلثی بالا و یک اسکالر مثلث بالایی است.

ماتریسی از شکل

بالا مثلثی یا ماتریس مثلثی چپ نامیده می شود و به طور مشابه ماتریس به شکل

پایین مثلثی یا ماتریس مثلثی راست نامیده می شود . یک ماتریس مثلثی پایین یا چپ معمولاً با متغیر L و یک ماتریس مثلثی بالا یا راست معمولاً با متغیر U یا R نشان داده می شود .

مثالها [ ویرایش ]

این ماتریس

بالا مثلثی است و این ماتریس

پایین مثلثی است