مثال: اگر نیروی خالص  F 2 وارد بر q 2 باشد بار q 3 را بر حسب q پیدا کنید؟

مثال: اگر بار q 2 حرکت نمی کند، بار q 3 را بر حسب q پیدا کنید؟

چهار بار در یک مربع با اضلاع به طول 2.5 سانتی متر مرتب شده اند. دو بار در گوشه سمت راست بالا و پایین سمت چپ +3.0 × 10 -6 درجه سانتیگراد هستند. بارها در دو گوشه دیگر 3.0 - 10 -6 درجه سانتیگراد هستند . نیروی خالص وارد شده به بار در گوشه بالا سمت راست چقدر است. توسط سه اتهام دیگر؟

برای حل هر مشکلی مانند این، ساده ترین کار این است که یک نمودار خوب رسم کنید که نیروهای وارد بر بار را نشان دهد. شما همچنین باید اجازه دهید نمودار شما علائم شما را مدیریت کند. نیرو یک بردار است و هر زمانی که علامت منهای مرتبط با یک بردار داشته باشید تنها کاری که انجام می دهد این است که جهت بردار را به شما بگوید. اگر فلش‌هایی را دارید که جهت را در نمودارتان به شما می‌دهند، می‌توانید هر علامتی را که از معادله قانون کولن خارج می‌شود، رها کنید.

نیروهای وارد شده به بار در بالا سمت راست توسط سه مورد دیگر را در نظر بگیرید:

برای بدست آوردن نیروی خالص باید بسیار مراقب باشید که این نیروها را به عنوان بردار اضافه کنید. در این مسئله می‌توانیم از تقارن استفاده کنیم و نیروهای بارهای 2 و 4 را به نیرویی در امتداد مورب (مخالف نیروی بار 3) با قدر 183.1 نیوتن ترکیب کنیم. وقتی این نیرو با نیروی 64.7 نیوتن ترکیب شود. در جهت مخالف، نتیجه نیروی خالص 118 نیوتن است که در امتداد مورب مربع قرار دارد.

تقارن در اینجا کار را کمی ساده تر می کند. اگر خیلی متقارن نبود، تنها کاری که باید انجام دهید این است که بردارها را به اجزای x و y تقسیم کنید، آنها را اضافه کنید تا اجزای x و y نیروی خالص را بیابید و سپس مقدار و جهت نیروی خالص را محاسبه کنید. نیروی خالص از اجزاء مثال 16-4 در کتاب درسی این روند را نشان می دهد.

منبع

http://physics.bu.edu/py106/notes/Coulomb.html

در قسمت های قبل یاد گرفتیم که بارهای یکسان یکدیگر را دفع می کنند و بارهای مخالف یکدیگر را جذب می کنند. آزمایش‌های انجام‌شده روی این موضوع نشان می‌دهد که این نیرو به فاصله بین بارها و میزان بارها بستگی دارد.

اگر فاصله بین جسم باردار افزایش یابد، مقدار جاذبه یا دافعه کاهش می یابد. در مقابل، اگر فاصله بین آنها کاهش یابد، مقدار نیرو افزایش می یابد. علاوه بر این، نیروهای الکتریکی با مقدار بار خالص نسبت مستقیم دارند.

اگر اجسام دارای یک نوع بار باشند، نیرو دافعه است و اگر بارهای مخالف داشته باشند، نیرو جاذبه است.

نیروی دافعه یا جاذبه الکتریکی از نظر قدر مساوی است اما در جهت مخالف است و به قدر بستگی ندارد.

F 12 =-F 21

تصویر داده شده در بالا نیروهایی را نشان می دهد که بر روی بارها عمل می کنند. F21 نیروی دافعه F2 روی F1 است. F12 نیروی F1 بر F2 است. همانطور که قبلاً گفتم؛

F 12 =-F 21

قانون کولمب: تعریف، فرمول و ثابت

8 نوامبر 2020 توسط Electrical4U

فهرست

قانون کولمب چیست؟

قانون کولن (همچنین به عنوان قانون مربع معکوس کولن شناخته می شود ) یک قانون فیزیک است که مقدار نیروی بین دو ذره ثابت و باردار الکتریکی (معروف به نیروی الکترواستاتیک ) را تعیین می کند. قانون کولن توسط چارلز آگوستین دو کولن در سال 1785 کشف شد. از این رو قانون و فرمول مربوطه به نام او نامگذاری شد.

تعریف قانون کولمب

قانون کلمب بیان می کند که بزرگی نیروی الکترواستاتیکی جاذبه یا دافعه بین دو جسم باردار الکتریکی با حاصلضرب بار اجسام باردار نسبت مستقیم دارد و با مجذور فاصله بین مرکز اجسام باردار نسبت عکس دارد.

این رابطه معکوس مربع به همین دلیل است که از این قانون به عنوان قانون مربع معکوس کولن نیز یاد می شود .

این مفهوم زمانی که برای اولین بار معرفی شد گیج کننده بود. نگاه کردن به فرمول قانون کولن در زیر می تواند به شما کمک کند تا رابطه بین بار و فاصله و چگونگی تأثیر آن بر نیروی الکترواستاتیک را تجسم کنید (نیروی الکترواستاتیک نیروی الکتریکی بین اجسام باردار در حالت سکون است. این به عنوان نیروی کولن نیز شناخته می شود).

فرمول قانون کولن

بیایید تصور کنیم، Q 1 و Q 2 بارهای الکتریکی دو جسم هستند.
d فاصله بین مرکز اجسام است.

اجسام باردار در یک محیط گذرا ε o ε r قرار می گیرند

سپس می توانیم نیروی F را به صورت زیر بنویسیم:

معادله بالا فرمول قانون کولن است. این فرمول به ما امکان می دهد نیروی الکترواستاتیکی را که دو بار به یکدیگر وارد می کنند محاسبه کنیم.

قانون اول کولمب

قانون اول کولن بیان می کند که اجسام دارای بار مشابه (جسم یا ذرات) یکدیگر را دفع می کنند و اجسام باردار با بار مخالف (جسم یا ذرات) یکدیگر را جذب می کنند.

قانون دوم کولمب

قانون دوم کولن بیان می کند که نیروی جاذبه یا دافعه بین دو جسم باردار الکتریکی با بزرگی بار آنها نسبت مستقیم و با مجذور فاصله بین آنها نسبت معکوس دارد. از این رو، طبق قانون دوم کولن،

جایی که،

1. "F" نیروی دافعه یا جاذبه بین دو جسم باردار است.
2. 'Q 1 ' و 'Q 2 ' بار الکتریکی اجسام هستند.
3. 'd' فاصله بین مرکز دو جسم باردار است.
4. 'k' ثابتی است که به محیطی که اجسام باردار در آن قرار می گیرند بستگی دارد. در سیستم SI و همچنین در سیستم MKS k=1/4πε o ε r . بنابراین معادله فوق تبدیل می شود.

مقدار ε o = 8.854 × 10^ -12 C 2 /Nm 2 .

از این رو، قانون کولن را می توان برای رسانه به صورت زیر نوشت:

سپس، در هوا یا خلاء ε r = 1. بنابراین، قانون کولن را می توان برای محیط هوا به صورت زیر نوشت:

مقدار ε r به محیط بستگی دارد. بیان گذردهی نسبی ε r به شرح زیر است.

اصل قانون کولن

فرض کنید اگر دو جسم باردار داشته باشیم که یکی بار مثبت و دیگری بار منفی داشته باشد، اگر در فاصله معینی از یکدیگر نگه داشته شوند، یکدیگر را جذب خواهند کرد. حال اگر بار یک جسم را افزایش دهیم و جسم دیگر را بدون تغییر نگه داریم، واضح است که نیروی جاذبه افزایش می یابد.

به همین ترتیب، اگر بار جسم دوم را افزایش دهیم و جسم اول را بدون تغییر نگه داریم، نیروی جاذبه بین آنها دوباره افزایش می یابد. از این رو، نیروی بین اجسام باردار متناسب با بار هر جسم یا هر دو است.

حالا با ثابت نگه داشتن شارژ آنها در Q 1 و Q 2 اگر آنها را به هم نزدیکتر کنید نیروی بین آنها افزایش می یابد و اگر آنها را از یکدیگر دور کنید نیروی وارده بین آنها کاهش می یابد.

اگر فاصله بین دو جسم بار d باشد، می توان ثابت کرد که نیروی وارد بر آنها با d^ 2 نسبت معکوس دارد.

این رشد نیرو بین دو جسم باردار یکسان در همه رسانه ها یکسان نیست. همانطور که در فرمول های بالا بحث کردیم، ε r برای محیط های مختلف تغییر می کند. بنابراین، بسته به رسانه، ایجاد نیرو می تواند متفاوت باشد.

محدودیت های قانون کولن

1. اگر میانگین تعداد مولکول های حلال بین دو ذره بار جالب باید زیاد باشد، قانون کولن معتبر است.
2. قانون کولن در صورتی معتبر است که بارهای نقطه ای در حال ساکن باشند.
3. هنگامی که بارها به شکل دلخواه هستند، اعمال قانون کولمب دشوار است. بنابراین، ما نمی توانیم مقدار فاصله 'd' بین بارها را زمانی که به شکل دلخواه هستند تعیین کنیم.

چه کسی قانون کولن را اختراع کرد؟

قانون کولن اولین بار در سال 600 قبل از میلاد توسط فیلسوف یونانی تالس اهل میلتوس مشاهده شد. اگر دو جسم با الکتریسیته ساکن شارژ شوند، بسته به ماهیت بار خود، یکدیگر را دفع یا جذب می کنند. این فقط یک مشاهده بود اما او هیچ رابطه ریاضی برای اندازه گیری نیروی جاذبه یا دافعه بین اجسام باردار ایجاد نکرد.

پس از قرن ها، در سال 1785، چارلز آگوستین دو کولمب، فیزیکدان فرانسوی، رابطه ریاضی واقعی بین دو جسم باردار الکتریکی را منتشر کرد و معادله ای برای نیروی دافعه یا جاذبه بین آنها استخراج کرد. این رابطه اساسی بیشتر به عنوان قانون کولن شناخته می شود.

منبع

https://www.electrical4u.com/coulombs-law/

دو ذره با بارهای 000003/. و 000015/. کولن به فاصله 12 سانتی متر قرار گرفته اند بزرگی نیروی الکتروستاتیکی بین دو ذره را حساب کنید

حرکت یک جسم پرتابه تحت تأثیر گرانش است. استفاده از فرمول ها برای محاسبه حرکت پرتابه افقی و عمودی با گلوله توپ و مسائل تمرین برج ایفل را تمرین کنید. 

حرکت پرتابه چیست؟

قطرات باران که از آسمان می‌بارد و توپ بیس‌بال که در هوا پرواز می‌کند چه وجه اشتراکی دارند؟ حرکت پرتابه!

حرکت پرتابه را می توان حرکتی دانست که در آن یک جسم تنها تحت تأثیر نیروی گرانش در فضا در حال حرکت است. این جسم متحرک می تواند از هر اندازه، شکل و ترکیب ماده ای باشد و خود به آن پرتابه می گویند .

اگرچه در بسیاری از موقعیت‌های دنیای واقعی، نیروهای کوچک دیگری ممکن است درگیر باشند، مانند مقاومت هوا که حرکت بیس‌بال را به تاخیر می‌اندازد، ما به خاطر سادگی، این نیروهای دیگر را ناچیز فرض می‌کنیم.

بیایید به چند مثال از کاربرد فرمول های حرکت پرتابه در مسائل دنیای واقعی نگاه کنیم.

راهبرد کلی برای حل مسائل حرکت پرتابه این است که مسئله را بخوانید و مطمئن شوید که چه اتفاقی می افتد، کمیت های شناخته شده و مجهول را یادداشت کنید، و با انتخاب معادله ای که دارای کمیت های مجهول شما باشد، برای یک کمیت مجهول حل کنید. جستجو برای، اما نه دیگران.

حرکت افقی و عمودی

برای حل مسائل حرکت پرتابه، باید چند نکته را در نظر داشته باشیم. اول، سرعت افقی پرتابه باید ثابت بماند، زیرا گرانش فقط در جهت عمودی عمل می کند. این ما را به فرمول های زیر هدایت می کند:

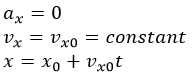معادله بالا به ما می گوید که شتاب افقی صفر است. در نتیجه، سرعت افقی در هر زمان ثابت و برابر با سرعت افقی اولیه است، همانطور که در معادله دوم نشان داده شده است. در فرمول پایین، x ، مسافت افقی، برابر با فاصله افقی اولیه، x o ، به اضافه حاصل ضرب سرعت افقی، v o و زمان سفر، t است.

در جهت عمودی چطور؟ خوب، از آنجایی که اکنون باید نیروی گرانش رو به پایین را محاسبه کنیم، فرمول ها به شرح زیر است:

شتاب عمودی مقدار ثابتی برابر با منهای g دارد، که در آن g شتاب ناشی از گرانش، 9.8 متر بر ثانیه در سیاره ما است. فرمول دوم به ما می گوید که سرعت عمودی نهایی، v y ، برابر است با سرعت عمودی اولیه، v o ، منهای g ضربدر t .

در معادله سوم، موقعیت عمودی نهایی، y ، برابر با موقعیت عمودی اولیه، y o ، به اضافه v yo ضربدر t منهای نصف g ضربدر t مربع را داریم. سرعت عمودی نهایی مجذور v y مجذور، برابر است با سرعت عمودی اولیه مجذور، v o مجذور، منهای 2 برابر g برابر مقدار y منهای y o .

با وجود این چیزهای بالقوه خسته کننده، اما همچنان مهم، بیایید به چند نمونه جالب برسیم. فقط مطمئن شوید که قبل از دیدن راه حلی که این درس ارائه می دهد، هر مسئله را خودتان امتحان کنید. به یک دلیل به آن می گویند تمرین!

مسئله تمرین توپ 

تصور کنید که یک گلوله توپ را از یک تپه 60 متری به زمین زیر شلیک کنید. فرض کنید سرعت گلوله توپ 25 متر بر ثانیه است، با زاویه 40 درجه نسبت به افقی شلیک می شود، و مطمئن هستید که هیچ کس در زمین پایین نیست.

همانطور که در تصویر زیر نشان داده شده است، مسافت افقی را که طی می کند، حداکثر ارتفاع آن، و کل زمان سفر تا زمانی که گلوله توپ به زمین برخورد می کند، محاسبه کنید:

برای هر یک از مجهولاتی که در حال حل آنها هستیم (زمان، حداکثر ارتفاع و کل محدوده افقی)، ترفند این است که معادله ای را انتخاب کنیم که فقط شامل یک مجهول باشد. می توانید ببینید که چندین مورد مختلف در مثال ما وجود دارد:

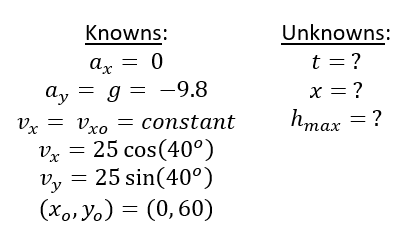کل زمان سفر را می توان با استفاده از این معادله محاسبه کرد زیرا حاوی مجهولات t است اما مجهولات x یا h max را شامل نمی شود :

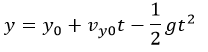با اتصال 60 برای ارتفاع عمودی اولیه، 25 برابر سینوس 40 درجه برای سرعت عمودی اولیه، و 9.8 برای g ، معادله درجه دوم را به دست می آوریم:

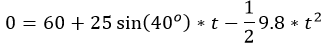قانون بقای حرکت
حرکت کلی یک سیستم مجزا از اجسام ثابت می ماند

m1v1 + m2v2 = m1v1' + m2v2'

•  یک گلوله کیلوگرمی با سرعت 200 متر بر ثانیه از یک تفنگ 6 کیلوگرمی شلیک می شود. سرعت پس زدن تفنگ چقدر است (جهت آن را در نظر بگیرید)؟
• یک توپ 10 گرمی و 30 گرمی در داخل لوله ای قرار می گیرد که یک فنر فشرده بین آنها وجود دارد. هنگامی که فنر آزاد می شود، توپ 10 گرمی با سرعت 6.0 متر بر ثانیه از لوله خارج می شود.سرعت توپ 30 گرمی را محاسبه کنید.آیا باید در جهت مخالف باشد؟
• یک واگن راه‌آهن 10000 کیلوگرمی که با سرعت 24 متر بر ثانیه حرکت می‌کند به یک واگن مشابه که ساکن است برخورد می‌کند. با هم قفل می کنند. سرعت متداول بعد از آن چقدر خواهد بود؟
   

یک توپ گلف 100.0 گرمی از ارتفاع 2 پرتاب می شود
 

سرعت توپ را درست هنگام برخورد با زمین محاسبه کنید. (6.26 متر بر ثانیه)

تکانه را محاسبه کنید. (1.2 کیلوگرم متر بر ثانیه)

سرعت برگشت توپ را درست در زمانی که به عقب بازمی‌گردد، محاسبه کنید. (5.74 متر بر ثانیه)

ارتفاع برگشت توپ را محاسبه کنید. (1.68 متر)
 

یک توپ بیسبال 150.0 گرمی با سرعت 20.0 متر بر ثانیه پرتاب می شود
یک گرم بیسبال با سرعت 20 متر بر ثانیه پرتاب می شود. نیروی برهمکنش در مقابل زمان در نمودار زیر نشان داده شده است.

تکانه را محاسبه کنید. (4.50 کیلوگرم متر بر ثانیه)

سرعت برگشت بیس بال را محاسبه کنید. (10.0 متر بر ثانیه)

یک توپ گلف 50 گرمی با نیروی 2400 نیوتن کوبیده می شود. توپ با سرعت 44 متر بر ثانیه به پرواز درآمد. چقدر با توپ در تماس بود؟