گرادیان یک تابع (یا میدان) اسکالر تابعی با مقدار برداری است که به سمت جهت سریع‌ترین افزایش تابع و با بزرگی برابر با سریع‌ترین افزایش در آن جهت هدایت می‌شود . آن را با نماد ∇ نشان می‌دهند (که در یونانی برای چنگ فنیقی نامیده می‌شود nabla ). بنابراین گرادیان یک مشتق جهت دار است .

یک تابع اسکالر یک عدد (یک مقدار اسکالر) را به هر نقطه از فضا مرتبط می کند.
یک تابع با ارزش برداری (یا تابع برداری) یک بردار را به هر نقطه از فضا مرتبط می کند.

دو میدان اسکالر در شکل بالا نشان داده شده است (یکی سمت چپ دارای تقارن دایره ای است). همانطور که می بینید، مقدار فیلد افزایش می یابد (برای قسمت چپ به سمت داخل و برای قسمت راست از سمت راست به چپ). بردارها (تابع با مقدار برداری) نشان دهنده گرادیان هستند و به سمت جهت سریعترین افزایش تابع اسکالر هدایت می شوند.

یک مثال از گرادیان، به عنوان مثال، تغییر دمای داخل یک اتاق است. دما یک کمیت اسکالر است، بنابراین می‌توانیم آن را به صورت ریاضی به صورت تابع f (x,y,z) نشان دهیم. برای هر نقطه (x,y,z) اتاق، تابع f یک عدد (دمای این نقطه) را برمی گرداند.

برای ساده کردن آن، دما را در زمان ثابت در نظر می گیریم. اگر گرادیان f را در یک نقطه (x,y,z) محاسبه کنیم، تابع با مقدار برداری حاصل، جهت سریع‌ترین افزایش دما را در این نقطه برمی‌گرداند . قدر گرادیان با نرخ افزایش دما در این جهت مطابقت دارد.

نحوه محاسبه گرادیان به سیستم مختصات مورد استفاده بستگی دارد.

گرادیان در مختصات دکارتی :

در جایی که نماد ∂ مشتق جزئی تابع f را با توجه به متغیر مربوطه نشان می دهد. هنگامی که یک تابع اسکالر به چندین متغیر وابسته است، مشتق جزئی آن نسبت به یک متغیر با ثابت نگه داشتن متغیرهای دیگر محاسبه می شود.

i ، j و k به ترتیب بردارهای واحد برای جهات x، y و zهستند

مثالی از مشتقات جزئی یک تابع اسکالر :

و شیب آن:

گرادیان در مختصات کروی :

مختصات کروی در شکل زیر نشان داده شده است:

و گرادیان تابع f که در مختصات کروی بیان می شود به صورت زیر بدست می آید:

جایی که u r ، u θ و u φ بردارهای واحد برای جهات r، θ y φ هستند.

وقتی تابع f فقط به مختصات شعاعی (مثلاً انرژی پتانسیل الکترواستاتیکی) بستگی دارد، گرادیان آن با:

در جایی که نماد مشتق کل d به جای مشتق جزئی ∂ استفاده می شود زیرا در اینجا f فقط به یک متغیر منفرد (r) بستگی دارد.

روز دیگر با یکی از دانش آموزان در مورد ماتریس های چرخشی گپ طولانی ای داشتم. آنها در درس فیزیک مهندسی به نام دینامیک به عنوان راهی برای یافتن اجزای بردارها نسبت به محورهای چرخیده مطرح شده بودند. او چند یادداشت از یکی از معلمان MLC من روی یک تکه کاغذ خط خورده بود که متأسفانه در واقع برای وضعیت او درست نبود. من دقیقاً می‌دانم چرا این اتفاق افتاد: ماتریس‌های چرخشی هم در Dynamics و هم در Maths 1B استفاده می‌شوند، اما آنها به روش‌های مختلفی استفاده می‌شوند (در واقع، دو کاربرد متفاوت فقط در Maths 1B وجود دارد!). وقت آن است که برای رفع این سردرگمی تلاش کنم، به خصوص که سه دانشجوی دیگر در هفته گذشته دقیقاً در مورد این موضوع از من سؤال کرده اند!

در Maths 1B، شما در مورد تبدیل های خطی ، که نوع خاصی از تابع هستند که بر بردارها در برخی ابعاد اعمال می کنید تا بردارهایی را در برخی ابعاد تولید کنید، یاد می گیرید. به نظر می رسد که تمام تبدیل های خطی را می توان با نمایش بردار  به عنوان ستونی از مختصات و ضرب آن در یک ماتریس توصیف کرد. هر تبدیل خطی ماتریس مخصوص به خود را دارد که برای همه بردارهایی که روی آنها عمل می کند کار می کند. چرخش‌ها یک نوع تبدیل خطی هستند و در دو بعد فرمولی بر اساس زاویه‌ای که می‌چرخانید وجود دارد که به شما می‌گوید ماتریس چیست. من فقط چنین ماتریسی را در تصویر اینجا قرار داده ام.

یکی از دلایل این کار این است که ضرب یک ماتریس در بردارهای پایه استاندارد (1,0) T و (0,1) T به ترتیب ستون های اول و دوم ماتریس را به شما می دهد. اما ضرب در ماتریس همان اثر تبدیل چرخش را دارد، بنابراین برای اینکه بفهمیم این ستون ها واقعا چه هستند، تنها کاری که باید انجام دهیم این است که نقاط (1,0) و (0,1) را بچرخانیم. اگر این کار را انجام دهید، به دلیل مثلثات، دو نقطه

(cos θ، sin θ) و (-sin θ، cos θ)

به دست می‌آید که در واقع ستون‌های ماتریس هستند.

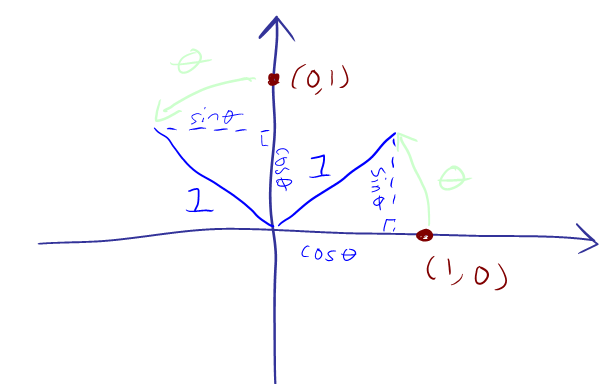
اجازه دهید قبل از حرکت مطمئن شویم که اینجا چه خبر است: شما یک نقطه در صفحه دوبعدی دارید، مختصات آن را به عنوان یک ستون در نظر می گیرید، این ستون را در ماتریس ضرب می کنید، و مجموعه جدیدی از مختصات را تولید می کنید. یک نکته جدید است بنابراین ماتریس شما در واقع نقطه شما را از یک مکان به مکان دیگر منتقل می کند . نقطه با مختصات (1,0) به نقطه دارای مختصات حرکت می کند

 (cos θ، sin θ).

 نقطه با مختصات (0،1) به نقطه دارای مختصات

(-sin θ، cos θ) 

حرکت می کند .

بنابراین اکنون داریم که یک ماتریس چرخشی دارای cos θ در مورب اصلی، sin θ در گوشه پایین سمت چپ و – sin θ در گوشه بالا سمت راست است. و به شما می گوید که یک نقطه با چرخش θ در خلاف جهت عقربه های ساعت به کجا می رود. (شایان ذکر است که بر روی اجزای بردارهایی که به صورت فلش تصور می شوند نیز به خوبی کار می کند.)

مشکل این است که در دینامیک، یک ماتریس چرخش کاملاً شبیه این نیست! به طور خاص، علامت منفی در گوشه مقابل است. چرا؟

پاسخ این است که در دینامیک، ماتریس چرخش توصیفی از تبدیل خود نقاط یا فلش ها نیست، بلکه توصیفی از چگونگی تغییر مختصات آنها هنگام تبدیل محورهای مختصات است . خود نقاط اصلا حرکت نمی کنند، این محورهای مختصات هستند که حرکت می کنند و ما فقط نقاط را با مختصات جدید دوباره برچسب می زنیم.

دلیل اینکه این کار مجدداً به دلیل بردارهای پایه استاندارد است. نقطه (1,0) با توجه به محورهای جدید مختصات آن دوباره محاسبه می‌شود و مختصات آن (cos θ, -sin θ) است. در حالی که نقطه (0،1) نیز مختصات آن دوباره محاسبه شده و مختصات آن (sin θ، cos θ) است.

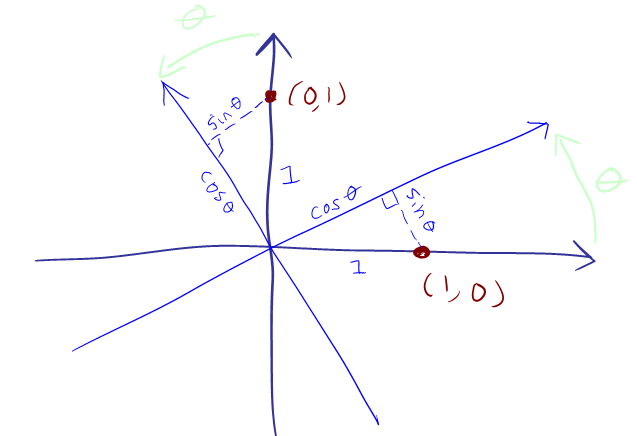
ممکن است متوجه شوید که این دقیقاً همان چیزی است که مختصات اگر خود نقاط را بچرخانید، اما در جهت مخالف ماتریس چرخش اصلی است. این منطقی است. اگر سر خود را بچرخانید تا با محورهای مختصات جدید مطابقت داشته باشد، دقیقاً این اتفاق افتاده است. اساساً، اگر محورهای مختصات را به یک جهت بچرخانید، نقاط نسبت به محورها به سمت دیگری حرکت می کنند.

و این پایان داستان خواهد بود، با این تفاوت که در شما محورهای مختصات را نیز می چرخانید، و با این حال، ماتریس چرخش به نوعی هنوز مانند آنچه در دینامیک وجود دارد، نیست! چرا؟

دلیل آن این است که در ریاضیات 1B محورها را در چارچوب معادلات منحنی می‌چرخانیم، و این وضعیت کاملاً متفاوت از زمانی است که شما محورها را در بافت خود نقاط می‌چرخانید.

تصور کنید من معادله ای دارم که یک منحنی را توصیف می کند. یک نقطه اگر مختصات آن معادله را برآورده کند بخشی از منحنی است و اگر مختصات آن معادله را برآورده نکند بخشی از منحنی نیست . اما اگر همه نقاط را با مختصات جدید با توجه به مجموعه جدیدی از محورها دوباره برچسب بزنم چه می شود؟ من یک معادله برای منحنی خود می خواهم به طوری که یک نقطه در منحنی باشد اگر مختصات جدید آن معادله جدید را برآورده کند. چگونه به آن دست پیدا کنم؟ خوب من قبلاً یک معادله دارم، فقط از نظر مختصات قدیمی است. بنابراین اگر نقطه ای در مختصات جدید داشته باشم، برای اینکه بگویم در منحنی است یا نه، فقط باید بفهمم مختصات قدیمی چیست و زیر آنهابه معادله قدیمی باید بتوان یک معادله ایجاد کرد که هر دوی این اقدامات را در بر گیرد - انتقال به سیستم مختصات قدیمی و فرورفتن در معادله قدیمی.

متوجه شدی آنجا چه گذشت؟ برای ایجاد معادله ای که همان منحنی را نسبت به محورهای جدید توصیف می کند، مجبور شدم با مختصات جدید شروع کنم و آنها را به مختصات قدیمی تبدیل کنم . بگذارید تکرار کنم: باید از جدید به قدیمی می رفتم . ماتریس تبدیل مختصات در دینامیک از قدیمی به جدید می رود. برای رفتن در جهت مخالف باید منهای را در گوشه مخالف داشته باشم.

بنابراین به همین دلیل است که ماتریس ها متفاوت هستند. در دینامیک شما محورها را جابه جا می کنید اما نقاط را نه، و مختصات جدیدی برای نقاط پیدا می کنید. در ریاضیات 1B شما نقاط را حرکت می دهید، نه محورها، بنابراین به نظر می رسد که چرخش در جهت دیگر باشد. یا در ریاضیات 1B محورها را جابه‌جا می‌کنید ، اما از قبل مختصات جدید را می‌دانید و مختصات قدیمی را می‌خواهید، بنابراین در واقع محاسبه را در جهت مخالف انجام می‌دهید.

برای تمامی xهای حقیقی و مختلط، رابطه‌های زیر برقرار است:

معادلات دیفرانسیل یک معادله ریاضی است و بیانگر یک تابع مجهول از یک یا چند متغیر مستقل و مشتق‌های مرتبه‌های مختلف آن نسبت به متغیرهای مستقل می‌باشد. فرض کنید f تابعی معین از x, y و مشتقات y باشد. در این صورت معادله‌ای به فرم زیر:

یک معادلهٔ دیفرانسیل معمولی صریح از مرتبهٔ n نامیده می‌شود. در حالت کلی تر فرم ضمنی معادلهٔ دیفرانسیل معمولی از مرتبهٔ n به صورت زیر می‌باشد:

به‌طور کل معادلات دیفرانسیل به سه روش تحلیلی، نیمه تحلیلی و عددی قابل حل می‌باشد.

مشتق توابع پارامتری

توابع که به فرم  هستند را توابع پارامتری می‌نامند. در این حالت، مشتق نسبت به \ از رابطهٔ زیر قابل محاسبه است:

مشتق کل

هرگاه  تابعی از به باشد، آنگاه مشتق جهت‌دار  در یک جهت بخصوص، بهترین تقریب خطی  در آن نقطه و جهت است. اما هرگاه  باشد، دیگر مشتق جهت‌دار نمی‌تواند به تنهایی، تصویر کاملی از رفتار تابع نشان دهد. مشتق کل، که دیفرانسیل کل نیز نامیده می‌شود با در نظر گرفتن رفتار تابع در تمام جهت‌ها می‌تواند تصویر کاملی از رفتار تابع ارائه کند.

برخلاف مشتق جزئی، در محاسبهٔ مشتق کل تابع  نسبت به متغیر ، متغیرهای دیگر ثابت در نظر گرفته نمی‌شوند بلکه به  بستگی خواهند داشت و مشتق کل به صورت زیر تعریف می‌شود:

مشتق کل در حساب دیفرانسیل با مفهومی مشابه، به یک عملگر دیفرانسیلی نیز گفته می‌شود. این عملگر دیفرانسیلی، مشتق کل تابع را نسبت  به صورت زیر محاسبه می‌کند:

مشتق جهت‌دار

مشتق جزئی تابع میزان تغییرات را در امتداد محورهای مختصات به دست می‌دهد در حالیکه مشتق جهت‌دار، سویی یا جهتی، میزان تغییرات  را در امتداد یک بردار دلخواه در فضا حساب می‌کند. اگر  در همسایگی نقطهٔ  تعریف شده باشد و برداری شامل نقطهٔ  باشد، مشتق جهت‌دار  در  به صورت زیر محاسبه می‌شود:

که در آن نقطهٔ باید متعلق به  باشد و فاصلهٔ علامت‌دار  تا  است یعنی اگر  و  هم‌جهت باشند  و در غیر این صورت  در نظر گرفته می‌شود.

مشتق ضمنی

در مقابل رابطهٔ صریح تابع به شکل کلی ، رابطهٔ ضمنی آن به صورت  قرار می‌گیرد. برای محاسبهٔ مشتق توابع ضمنی دو روش کلی وجود دارد:

• استفاده از قاعدهٔ زنجیری: در این روش، از طرفین رابطه نسبت به  مشتق می‌گیریم و با فاکتورگیری،  را بدست می‌آوریم. (اگر بخواهیم مشتق را نسبت به  حساب کنیم آنگاه  و  خواهد بود)
• استفاده از مشتق جزئی: در این روش از رابطهٔ زیر استفاده می‌شود:

در ریاضیات، تابع پیوسته در نقطه  تابعی است که در نقطه  تعریف شده، و همچنین حد تابع در آن نقطه موجود و برابر  باشد. در تعریفی شهودی خواهیم داشت تابعی پیوسته‌است که هر تغییر کوچک در ورودی اش، تغییری کوچک در خروجی اش ایجاد کند، و بتوان نمودار آن را بدون برداشتن قلم از روی کاغذ رسم کرد.

هر تابع به سه دلیل ممکن است پیوسته نباشد:

• حد تابع در آن نقطه موجود نباشد.
• تابع در آن نقطه موجود نباشد.
• حد موجود با مقدار تابع موجود، برابر نباشد.

تعریف هاینه[ویرایش]

تابع حقیقی پیوسته است، اگر به ازای هر دنباله  که، نتیجه بگیریم . ادوارد هاینه ریاضی‌دان آلمانی این تعریف را ارائه داده‌است.

تابع کوژ بر یک بازه

تابع کوژ[۱][۲] یا محدب، اگرچه لزوماً تابعی پیوسته نیست، ولی یک تابع حقیقی است که اگر دو نقطه دلخواه بر روی این تابع در نظر بگیریم، پاره‌خط پیونددهندهٔ این دو نقطه همواره بالای این نمودار جای می‌گیرد.

تابع‌های و تابع نمایی دو نمونه آشنا از توابع کوژ هستند

نرخ اونس طلا به قیمت دیروز یعنی یک هزار و ۶۵۳ دلار ارزش گذاری شد.

• هر گرم طلای خام ۱۸ عیاربر حسب دلار
• هر مثقال طلا 17 عیار بر حسب دلار