مدتی است می خواهم یک اتومبیل بخرم اما نمی دانم چه زمانی این کار را انجام دهم؟ لطفا من را هنمایی کنید.
منحنی تغییرات قیمت آن را در بدست آورید اگر دیدید قیمت به مینمم نزدیک است آقدام به خرید کنید
مفاهیم ریاضی مرتبط:
از قاعده تقسیم استفاده می کنیم
نقاط بحرانی مهم هستند زیرا مقادیر شدید توابع نمی توانند در جای دیگری رخ دهند. نقطه c یک نقطه بحرانی تابع f در نظر گرفته می شود اگر:
مشتقات مرتبه بالاتر با گرفتن مکرر مشتقات مشتقات حاصل به دست می آیند. بنابراین، مشتق دوم یک تابع، مشتق مشتق اول آن است و مشتق مرتبه n ممکن است با گرفتن مشتق از مشتق مرتبه st (n - 1) به دست آید. ممکن است از نمادهای مختلفی برای نشان دادن مشتقات متوالی استفاده شود:
مثال شماره 1 :
پنج مشتق اول sin x را بیابید .
راه حل شماره 1 :
مثال شماره 2 :
سه مشتق اول
4 x ^3 + 2 x + 6
را بیابید.
راه حل شماره 2 :
برای تابع متمایز f با یک تابع معکوس y = f ^− 1 ( x )، چنین است که:
مثال :
مشتق معکوس f ( x ) = x^ 3 + 1 را تعیین کنید
راه حل :
این آموزش به سه بخش تقسیم می شود؛ آن ها هستند:
به عبارت بسیار ساده، مشتق تابع f(x) نرخ تغییر آن را نشان می‌دهد و با f'(x) یا df/dx نشان داده می‌شود. بیایید ابتدا به تعریف آن و یک تصویر تصویری از مشتق نگاه کنیم.
تصویری از تعریف یک مشتق تابع
در شکل Δx نشان دهنده تغییر در مقدار x است. ما فاصله بین x و (x+Δx) را کوچکتر و کوچکتر می کنیم تا زمانی که بینهایت کوچک شود. بنابراین، ما محدودیت داریم (Δ𝑥 0). صورت‌گر f(x+Δx)-f(x) تغییر متناظر در مقدار تابع f را در بازه Δx نشان می‌دهد. این باعث می شود که مشتق تابع f در نقطه x، نرخ تغییر f در آن نقطه باشد.
نکته مهمی که باید به آن توجه داشت این است که Δx، تغییر x می تواند منفی یا مثبت باشد. از این رو:
0<|Δx|< 𝜖،
جایی که 𝜖 یک مقدار بی نهایت کوچک است.
مشتق یک تابع را می توان با f'(x) و df/dx نشان داد. نیوتن غول ریاضی از f'(x) برای نشان دادن مشتق یک تابع استفاده کرد. لایب نیتس، یکی دیگر از قهرمانان ریاضی، از df/dx استفاده کرد. بنابراین df/dx یک عبارت واحد است که نباید با کسری اشتباه گرفته شود. به عنوان مشتق تابع f نسبت به x خوانده می شود و همچنین نشان می دهد که x متغیر مستقل است.
یکی از متداول‌ترین نمونه‌هایی که از مشتقات ذکر شده، سرعت است. سرعت، میزان تغییر فاصله زمانی است. بنابراین اگر f(t) نشان دهنده مسافت طی شده در زمان t باشد، آنگاه f'(t) سرعت در زمان t است. بخش های زیر نمونه های مختلفی از محاسبه مشتق را نشان می دهد.
روش یافتن مشتق تابع را تمایز می گویند. در این بخش، خواهیم دید که چگونه می توان از تعریف مشتق برای یافتن مشتق توابع مختلف استفاده کرد. بعداً، وقتی با تعریف راحت‌تر شدید، می‌توانید از قوانین تعریف‌شده برای مشتق گیری یک تابع استفاده کنید.
بیایید با یک مثال ساده از یک تابع خطی m(x) = 2x+5 شروع کنیم. می‌توانیم ببینیم که m(x) با یک نرخ ثابت تغییر می‌کند. ما می توانیم این تابع را به صورت زیر مشتق گیری کنیم.
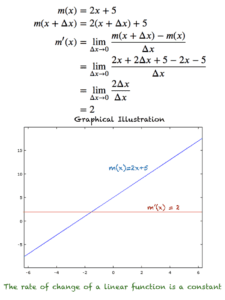
مشتق m(x) = 2x+5
شکل بالا نشان می دهد که تابع m(x) چگونه در حال تغییر است و همچنین نشان می دهد که مهم نیست کدام مقدار از x، نرخ تغییر m(x) را انتخاب می کنیم همیشه 2 باقی می ماند.
فرض کنید تابع g(x) را داریم: g(x) = x^2. شکل زیر نحوه محاسبه مشتق g(x) را نشان می دهد. همچنین نمودار تابع و مشتق آن در شکل وجود دارد.
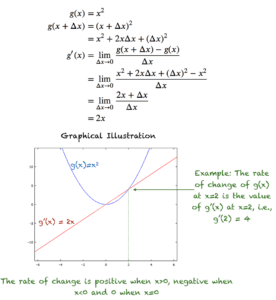
مشتق g(x) = x^2
به عنوان g'(x) = 2x، بنابراین g'(0) = 0، g'(1) = 2، g'(2) = 4 و g'(-1) = -2، g'(-2) = -4
از شکل می بینیم که مقدار g(x) برای مقادیر منفی بزرگ x بسیار بزرگ است . وقتی x <0، افزایش x باعث کاهش g(x) و از این رو g'(x) < 0 برای x<0 می شود. نمودار برای x=0 مسطح می شود، جایی که مشتق یا نرخ تغییر g(x) صفر می شود. هنگامی که x> 0، g(x) با افزایش x به طور درجه دوم افزایش می یابد، و از این رو، مشتق نیز مثبت است.
فرض کنید تابع h(x) = 1/x را داریم. در زیر مشتق h(x) (برای x ≠0) و شکلی که مشتق را نشان می دهد نشان داده شده است. منحنی آبی نشان دهنده h(x) و منحنی قرمز مشتق مربوط به آن است.
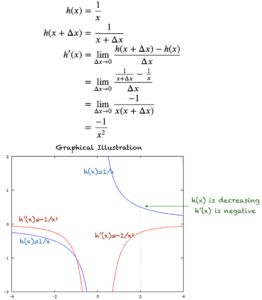
مشتق h(x) = 1/x
برای مثال 3، تابع h(x) = 1/x در نقطه x=0 تعریف نشده است. بنابراین، مشتق آن نیز در x=0 تعریف نشده است. اگر تابعی در نقطه ای پیوسته نباشد، در آن نقطه مشتق ندارد. در زیر چند سناریو وجود دارد که در آن یک تابع قابل مشتق گیری نیست:
در زیر چند نمونه آورده شده است:
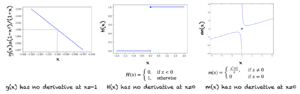
نمونه هایی از نقاطی که هیچ مشتقی در آنها وجود ندارد
این درس ها به مشتقات نمایی نگاه می کند.
نمودار زیر مشتقات توابع نمایی را نشان می دهد.
مشتق تابع نمایی طبیعی
می‌توانیم فرمول بالا را با قانون زنجیره ترکیب کنیم تا به دست آید
مثال:
مثال:
با استفاده از قانون ضرب و فرمول های بالا، به دست می آوریم
مثال:
مثال:
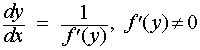
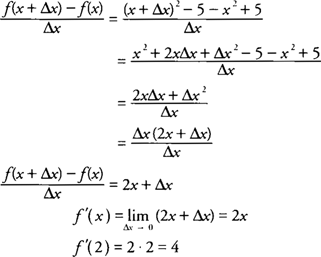
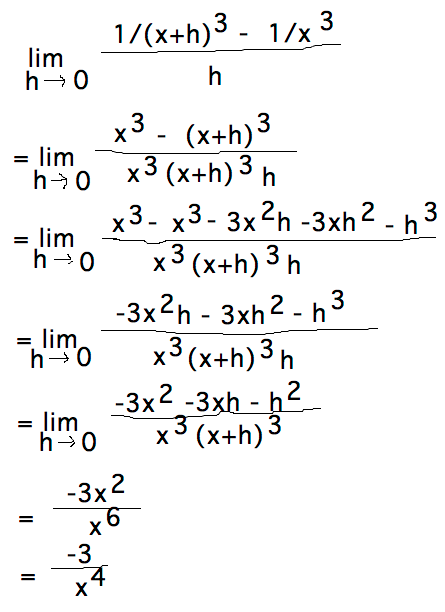
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
