۱۴۰۲/۰۵/۰۶ - - علی رضا نقش نیلچی -
اگر صفحه ای با عنوان "آزمون اولین مشتق" را خوانده باشید، می دانید که ما می توانیم از مشتق اول برای تعیین اینکه آیا یک نقطه بحرانی خاص در نمودار یک تابع حداکثر محلی، حداقل محلی یا هیچکدام از آنها استفاده کنیم. می دانیم که برای حداکثر محلی، شیب یک تابع (که در نهایت همان چیزی است که مشتق اول به ما می دهد) به سمت چپ حداکثر محلی (جایی که مقدار تابع در حال افزایش است) مثبت و به سمت راست منفی خواهد بود. حداکثر محلی (جایی که مقدار تابع در حال کاهش است ). برای حداقل محلی، دقیقا برعکس اتفاق می افتد. شیب رو به کاهش است سمت چپ حداقل محلی و افزایش به سمت راست حداقل محلی.
احتمالاً ارزش این را دارد که بیانیه رسمیتر ما را در توصیف اولین آزمون مشتق تکرار کنیم. فرض کنید یک تابع ƒ( x ) داریم که در بازه بسته [ a , b ] پیوسته است و در بازه باز ( a , b ) قابل تمایز است و یک مقدار c وجود دارد به طوری که a < c < b و ( c) وجود دارد. ، ƒ( c )) یک نقطه بحرانی از تابع ƒ( x ) است :
اگر ƒ′( x ) > 0 در سمت چپ ( c , ƒ( c )) و ƒ′( x ) < 0 در سمت راست ( c , ƒ( c )) باشد ، آنگاه ( c , ƒ( c )) حداکثر محلی است.
اگر ƒ′( x ) < 0 در سمت چپ ( c , ƒ( c )) و ƒ′( x ) > 0 در سمت راست ( c , ƒ( c )) باشد ، آنگاه ( c , ƒ( c )) حداقل محلی است.
اگر ƒ′( x ) در سمت چپ و راست ( c , ƒ( c )) علامت یکسانی داشته باشد ، آنگاه ( c , ƒ( c )) نه حداکثر محلی است و نه یک حداقل محلی.
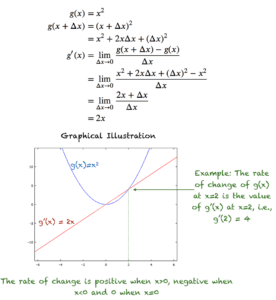
تصویر زیر را در نظر بگیرید. در اینجا نمودار تابع چند جمله ای ƒ( x ) = 2 x 5 - 10 x 3 و نمودار اولین تابع مشتق آن ƒ′( x ) = 10 x 4 - 30 x 2 را می بینیم . می بینیم که ƒ( x ) دارای دو منتهی الیه محلی است که در جایی رخ می دهند که نمودار ƒ′( x ) محور x را قطع می کند . همچنین دارای یک نقطه عطف در x = 0 است ، جایی که نمودار ƒ′( x ) x را لمس می کند.محور در یک نقطه است، اما آن را قطع نمی کند. از آنجایی که ƒ( x ) یک تابع چند جمله ای است و بنابراین "به خوبی رفتار می کند"، می توانیم تمام نقاط بحرانی آن را با حل ƒ'( x ) = 0 پیدا کنیم . سپس فقط باید اولین آزمون مشتق را برای هر نقطه اعمال کنیم تا مشخص کنیم که آیا حداکثر محلی است، یک حداقل محلی یا هیچکدام.
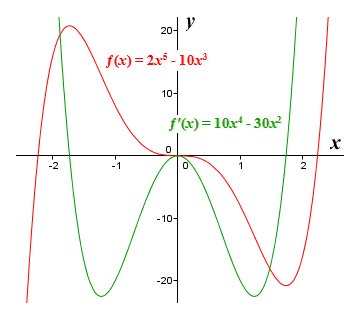
نمودارهای ƒ( x ) = 2 x 5 - 10 x 3 و ƒ′( x ) = 10 x 4 - 30 x 2
بنابراین، می دانیم که می توانیم ماهیت یک نقطه بحرانی را با بررسی علامت مشتق اول در دو طرف آن تعیین کنیم. برای اینکه تست کار کند، تابع باید در بازه زمانی تعریف شده پیوسته باشد. همچنین باید فوراً در سمت چپ و راست نقطه بحرانی که آزمون روی آن اعمال میشود قابل تمایز باشد، اگرچه لازم نیست اولین مشتق در خود نقطه بحرانی وجود داشته باشد. با این حال، اگر در آنجا وجود داشته باشد ، ممکن است بتوانیم ماهیت نقطه بحرانی را با استفاده از آزمون مشتق دوم به راحتی تعیین کنیم .
همانطور که خواهیم دید، مشتق دوم در یک نقطه از یک منحنی می تواند چیزی در مورد تقعر منحنی در آن نقطه به ما بگوید. به طور کلی، یک قطعه خط منحنی اگر تمام یا بخشی از یک کاسه را تشکیل دهد به سمت بالا مقعر گفته می شود و اگر تمام یا بخشی از یک گنبد را تشکیل دهد، به پایین مقعر گفته می شود. میتوانیم با نگاه کردن به نمودارهای تابع چند جملهای ƒ( x ) = 2 x 5 - 10 x 3 و مشتق اول آن را یک بار دیگر توضیح دهیم.
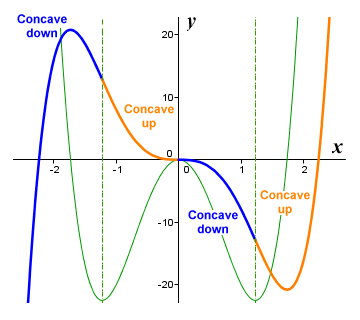
نمودار ƒ( x ) = 2 x 5 - 10 x 3 دارای هر دو ناحیه مقعر بالا و پایین مقعر است.
بیایید رابطه بین نمودار خود تابع و اولین مشتق آن را در نظر بگیریم. از تصویر بالا به وضوح میبینیم که برای بازههایی که نمودار تابع به پایین مقعر است، با افزایش x ، مقدار اولین مشتق کاهش مییابد . برعکس، برای بازههایی که نمودار تابع در آنها مقعر است، با افزایش x ، مقدار اولین مشتق افزایش مییابد . علاوه بر این، نقاطی که در آن تقعر تابع از مقعر به پایین به مقعر به بالا تغییر می کند، هر دو با حداقل های محلی مطابقت دارند.روی نمودار اولین مشتق به طور مشابه، نقطه ای که در آن تقعر تابع از مقعر به بالا به پایین مقعر تغییر می کند ، مطابق با حداکثر محلی در نمودار اولین مشتق است.
ممکن است قبلاً برای شما پیش آمده باشد که مشتق دوم یک تابع (که به یاد داشته باشید، به سادگی مشتق اولین مشتق تابع است) باید در هر انتها محلی از مشتق اول به صفر ارزیابی شود . در واقع قضیه همین است. این بدان معنی است که برای هر تابع پیوسته و دوبار متمایز (توجه داشته باشید که همه توابع را نمی توان دو بار متمایز کرد)، منطقی است که فرض کنیم با یافتن صفرهای تابع مشتق دوم، مختصات x نقاط عطف را به ما می دهد. نمودار تابع اصلی ما - یعنی نقاطی که در آنها تقعر آن از مقعر به پایین تغییر می کندمقعر کردن ، و بالعکس. ما در زیر نمودار تابع چند جمله ای ƒ( x ) = 2 x 5 - 10 x 3 را یک بار آخر، این بار همراه با نمودار تابع مشتق دوم آن ƒ′′( x ) = 40 x 3 - 60 x ارائه می کنیم .
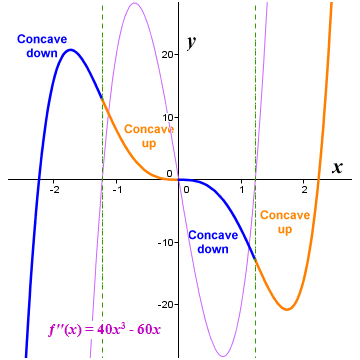
نمودارهای ƒ( x ) = 2 x 5 - 10 x 3 و ƒ′′( x ) = 40 x 3 - 60 x
مانند مشتق اول، مشتق دوم می تواند چیزی در مورد آنچه یک تابع در یک نقطه مشخص انجام می دهد به ما بگوید. قبلاً دیدهایم که مشتق دوم برای مقادیر x که با نقاط عطف مطابقت دارند (یعنی نقاطی که در آنها تقعر نمودار تابع تغییر میکند) به صفر میرسد. همچنین میتوانیم به وضوح از تصویر بالا ببینیم که برای فواصل زمانی که تابع به پایین مقعر است ، مقدار مشتق دوم منفی است . برای بازه هایی که تابع در آنها مقعر است ، مقدار مشتق دوم مثبت است .
بنابراین، میتوانیم از مشتق دوم استفاده کنیم تا به ما بگوییم که آیا یک تابع در هر نقطه از نمودار تابع مقعر است یا مقعر (یا هیچکدام) - البته به شرطی که تابع در آن نقطه دو بار متمایز باشد. میتوانیم این را کمی رسمیتر بیان کنیم (با استفاده از چیزی که گاهی به عنوان قضیه تقعر شناخته میشود ) به صورت زیر:
اگر یک تابع ƒ( x ) دو بار در x = c قابل تمایز باشد ، نمودار ƒ( x ) در ( c , ƒ(c) مقعر است.)) اگر ƒ′′( c ) > 0 , و مقعر اگر ƒ′′( c ) < 0 .
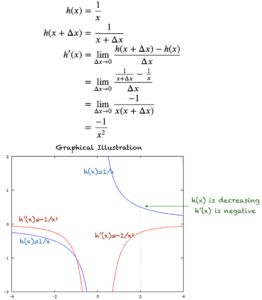
اگر مشتق دوم در یک نقطه معین صفر باشد یا وجود نداشته باشد، نقطه ممکن است یک نقطه عطف باشد، اما تنها در صورتی که تقعر نمودار در هر دو طرف نقطه متفاوت باشد. شرایطی وجود دارد که در آن مشتق دوم می تواند صفر ارزیابی شود و در عین حال یک نقطه عطف نباشد، همانطور که می بینیم اگر به تصویر زیر نگاه کنیم که نمودارهای تابع ƒ( x) = x 4 و مشتق دوم آن را نشان می دهد . ƒ′′( x ) = 12 x 2 .
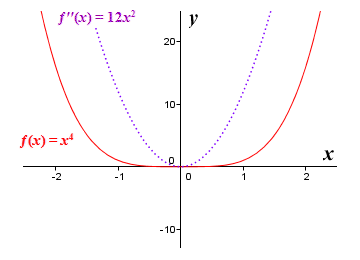
نمودارهای ƒ( x ) = x 4 و ƒ′′( x ) = 12 x 2
مشتق دوم تابع در x = 0 به صفر می رسد ، اما خود تابع در اینجا نقطه عطف ندارد. در واقع x = 0 مربوط به حداقل محلی است. شرایطی که تحت آن می توان از مشتقات اول و دوم برای شناسایی یک نقطه عطف استفاده کرد، ممکن است تا حدودی رسمی تر بیان شود، در مواردی که گاهی اوقات به عنوان قضیه نقطه عطف از آن یاد می شود ، به شرح زیر:
اگر نقطه ای در نمودار یک تابع ƒ( x ) وجود داشته باشد که برای آن x = c ، جایی که ƒ′( c ) وجود دارد و ƒ′′( x ) علامت را در x = c تغییر می دهد ، آنگاه نقطه ( c , ƒ( ج )) یک نقطه عطف در نمودار ƒ( x ) است . اگر ƒ′′( c ) در نقطه عطف وجود داشته باشد، ƒ′′( c ) = 0 .
ما میتوانیم نقاط عطف را با استفاده از مشتق دوم به روشی مشابه با روشی که در آن از مشتق اول برای آزمایش حداکثری محلی استفاده میکنیم، آزمایش کنیم. همانطور که قبلاً اشاره کردیم، میتوانیم از مشتق دوم برای تعیین اینکه آیا یک نقطه بحرانی یک تابع حداکثر محلی یا حداقل محلی است استفاده کنیم. با فرض اینکه بتوان از آن استفاده کرد، آزمون مشتق دوم جایگزین ساده تری برای آزمون مشتق اول ارائه می دهد. اشکال اصلی این است که تنها در صورتی می توان از آن استفاده کرد که معیارهای خاصی رعایت شود.
شاید قبلاً متوجه شده باشید که توانایی استفاده از مشتق دوم برای تعیین تقعر نمودار یک تابع در یک نقطه معین، چیزی است که ما را قادر می سازد از آن برای شناسایی یک نقطه بحرانی در یک تابع به عنوان حداکثر محلی یا یک تابع استفاده کنیم. حداقل محلی اگر در مورد آن فکر کنید، کاملاً واضح است که یک حداکثر محلی باید در قسمتی از نمودار که مقعر است رخ دهد (شما می توانید حداکثر محلی را در بالای یک تپه در نظر بگیرید). به همان اندازه بدیهی است که یک حداقل محلی باید در قسمتی از نمودار که به سمت بالا مقعر است رخ دهد (شما می توانید حداقل محلی را در پایین یک دره تصور کنید).
پس از شناسایی یک نقطه ثابت روی یک تابع، تنها کاری که ما باید انجام دهیم تا مشخص کنیم که حداکثر محلی یا حداقل محلی است، این است که مشتق دوم را در آن نقطه بگیریم. اگر مثبت باشد ، حداقل محلی داریم، زیرا نمودار در آن نقطه به سمت بالا مقعر است . اگر منفی باشد ، حداکثر محلی داریم، زیرا نمودار به پایین مقعر است . البته اگر مشتق دوم صفر باشد ، نمیتوانیم نتیجهگیری مفیدی داشته باشیم. در این صورت، ما باید چیز دیگری را امتحان کنیم، اما به زودی به آن باز خواهیم گشت. ما می توانیم آزمون مشتق دوم را به صورت رسمی تر توصیف کنیم:
برای یک تابع ƒ( x ) که دو بار در یک نقطه ثابت که برای آن x = c قابل تمایز است :
اگر ƒ′′( c ) > 0 , آنگاه ƒ( x ) دارای حداقل محلی در x = c است .
اگر ƒ′′( c ) < 0 , آنگاه ƒ( x ) دارای حداکثر محلی در x = c است .
اگر ƒ′′( c ) = 0 باشد ، آزمون بی نتیجه است.
همانطور که قبلاً بیان کردیم، قبل از استفاده از آزمون مشتق دوم، شرایط خاصی وجود دارد که باید رعایت شوند. شرط اول این است که هم مشتق اول و هم مشتق دوم باید در نقطه بحرانی که میخواهیم آزمایش کنیم وجود داشته باشند. با فرض انجام این کار، مشتق اول باید صفر ارزیابی شود، در حالی که مشتق دوم نباید صفر ارزیابی شود. به عبارت دیگر، برای یک نقطه بحرانی که در x = c رخ می دهد ، جملات ƒ′( c ) = 0 و ƒ′′( c ) ≠ 0 باید صادق باشند. اگر هر یک از این شرایط برآورده نشد، باید به پلان B برگردیم، که معمولاً به معنای استفاده از آن استاولین آزمون مشتق برای تعیین ماهیت نقطه بحرانی.
بیایید به یک مثال نگاه کنیم. ما سعی خواهیم کرد از آزمون مشتق دوم برای شناسایی حداکثر و مینیمم محلی تابع ƒ( x ) = x 4 - 8 x 2 استفاده کنیم . از آنجایی که این یک تابع چند جمله ای است، می دانیم که "به خوبی رفتار می کند". ما با یافتن نقاط بحرانی تابع شروع می کنیم، به این معنی که باید ریشه های اولین تابع مشتق را پیدا کنیم. با اعمال قوانین اساسی تمایز، دریافت می کنیم:
ƒ′( x ) = 4 x 3 - 16 x
حال باید معادله را حل کنیم:
4 x 3 - 16 x = 0
ما بلافاصله می توانیم عبارت 4 x را فاکتور کنیم :
4 x ( x 2 - 4) = 0
این مقادیر ممکن برای x از -2 ، 0 و 2 به ما می دهد . اکنون باید این مقادیر را به مشتق دوم متصل کنیم که با متمایز کردن مشتق اول آن را پیدا می کنیم. با اعمال قوانین اساسی تمایز، دریافت می کنیم:
ƒ′′( x ) = 12 x 2 - 16
با وصل کردن مقادیر x نقاط بحرانی خود به تابع مشتق دوم، دریافت می کنیم:
ƒ′′(-2) = (12)(-2 2 ) - 16 = 32
ƒ′′(0) = (12)(0 2 ) - 16 = -16
ƒ′′(2) = (12)(2 2 ) - 16 = 32
با اعمال آزمون مشتق دوم، متوجه میشویم که تابع ƒ( x ) = x 4 - 8 x 2 دارای حداقل محلی در x = -2 است (زیرا مشتق دوم در اینجا مثبت است)، حداکثر محلی در x = 0 (ثانیه مشتق منفی است)، و حداقل محلی دوم در x = 2 (مشتق دوم مثبت است). ما می توانیم مقادیر واقعی تابع را در این نقاط با وصل کردن مقادیر x به تابع اصلی پیدا کنیم:
ƒ(-2) = -2 4 - (8)(-2 2 ) = 16 - 32 = -16
ƒ(0) = 0 4 - (8) (0 2 ) = 0 - 0 = 0
ƒ(2) = 2 4 - (8) (2 2 ) = 16 - 32 = -16
بنابراین، در نمودار تابع ما حداقل های محلی در مختصات (2-, -16) و (2, -16) و حداکثر محلی در (0, 0) خواهیم داشت . ما در زیر نمودار تابع ƒ( x ) = x 4 - 8 x 2 را همراه با مشتقات اول و دوم آن ارائه می کنیم. برای این تابع، میتوانیم ببینیم که صفرهای مشتق دوم در واقع به نظر میرسد که با نقاط عطف در نمودار تابع مطابقت دارند. با این حال، همیشه اینطور نخواهد بود. همانطور که با نمودار تابع ƒ( x ) = x 4 دیدیم، صفرهای مشتق دوم نیز می توانند در حداکثر یا حداقل محلی یک تابع رخ دهند.
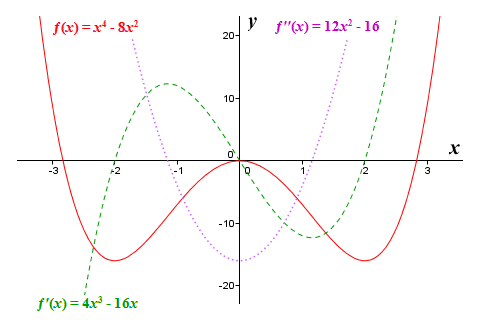
نمودارهای ƒ( x ) = x 4 - 8 x 2 ، ƒ′( x ) = 4 x 3 - 16 x و ƒ′′( x ) = 12 x 2 - 16
بیایید به مثال دیگری نگاه کنیم. این بار سعی می کنیم از مشتق دوم برای طبقه بندی نقاط بحرانی تابع ƒ( x ) = 3 x 5 - 5 x 3 + 3 استفاده کنیم . ما همچنین سعی خواهیم کرد نقاط عطف را شناسایی کنیم. یک بار دیگر، چون این یک تابع چند جمله ای است، می دانیم که "به خوبی رفتار می کند"، یعنی هم پیوسته و هم قابل تمایز برای تمام x ها خواهد بود . ابتدا مختصات x نقاط بحرانی تابع را با یافتن ریشه های اولین تابع مشتق بدست می آوریم . با اعمال قوانین اساسی تمایز، دریافت می کنیم:
ƒ′( x ) = 15 x 4 - 15 x 2
حال باید معادله را حل کنیم:
15 x 4 - 15 x 2 = 0
ما بلافاصله می توانیم عبارت 15 x 2 را در نظر بگیریم :
15 x 2 ( x 2 - 1) = 0
این مقادیر ممکن برای x از منهای یک ، صفر و یک به ما می دهد . حال باید این مقادیر را به مشتق دوم متصل کنیم که با متمایز کردن مشتق اول آن را پیدا می کنیم. با اعمال قوانین اساسی تمایز، دریافت می کنیم:
ƒ′′(x) = 60 x 3 - 30 x
با وصل کردن مقادیر x ، دریافت می کنیم:
ƒ′′(-1) = (60)(-1 3 ) - (-30) = -30
ƒ′′(0) = (60)(0 3 ) - 0 = 0
ƒ′′(1) = (60)(1 3 ) - 30 = 30
بنابراین، با اعمال آزمون مشتق دوم، متوجه میشویم که تابع ƒ( x ) = 3 x 5 - 5 x 3 + 3 دارای حداکثر محلی در x = -1 است (زیرا مشتق دوم در اینجا منفی است)، و حداقل محلی در x = 1 (که در آن مشتق دوم مثبت است). ما می توانیم مقادیر واقعی تابع را در این نقاط با وصل کردن مقادیر x به تابع اصلی پیدا کنیم:
ƒ(-1) = (3)(-1 5 ) - (5)(-1 3 ) + 3 = -3 - (-5) + 3 = 5
ƒ(1) = (3)(1 5 ) - (5)(1 3 ) + 3 = 3 - 5 + 3 = 1
از آنجایی که مشتق دوم در x = 0 به صفر ارزیابی می شود، آزمون مشتق دوم برای این نقطه بحرانی خاص بی نتیجه است. ما نمیتوانیم بگوییم که این یک حداکثر محلی، یک حداقل محلی یا یک نقطه عطف است، و در عوض باید به اولین آزمون مشتق برگردیم تا ماهیت آن مشخص شود. ما قبلا هم اولین تابع مشتق و هم لیستی از نقاط بحرانی تابع را بدست آورده ایم. فقط باید علامت اولین مشتق را بلافاصله در دو طرف x = 0 پیدا کنیم . ابتدا یک مقدار دلخواه بین منهای یک و صفر ( xمختصات دو نقطه بحرانی اول) و آن را به تابع مشتق اول وصل کنید. ما از منهای صفر-نقطه-پنج ( -0.5 ) استفاده می کنیم که به ما نشان می دهد:
ƒ′(-0.5) = (15)(-0.5 4 ) - (15)(-0.5 2 ) = -2.8125
بنابراین، اولین تابع مشتق یک مقدار منفی را بلافاصله در سمت چپ x = 0 برمی گرداند . حالا یک مقدار دلخواه بین صفر و یک ( مختصات x دو نقطه بحرانی آخر) را انتخاب می کنیم و آن را به تابع مشتق اول متصل می کنیم. ما از نقطه صفر پنج ( 0.5 ) استفاده می کنیم که به ما می دهد:
ƒ′(0.5) = (15)(0.5 4 ) - (15)(0.5 2 ) = -2.8125
بنابراین، اولین تابع مشتق نیز یک مقدار منفی را بلافاصله در سمت راست x = 0 برمی گرداند . بنابراین اولین آزمایش مشتق به ما می گوید که نقطه بحرانی در x = 0 نه حداکثر محلی است و نه یک حداقل محلی. اما آیا این یک نقطه عطف است؟ قضیه نقطه عطف را که در بالا بیان کردیم را به خاطر بسپارید . به ما می گوید که اگر نقطه ای در نمودار تابعی داشته باشیم که مشتق اول وجود داشته باشد و مشتق دوم علامت آن را تغییر دهد، آن نقطه باید یک نقطه عطف باشد. می دانیم که اولین مشتق در x = 0 وجود دارد. فقط باید بررسی کنیم که آیا مشتق دوم علامت آن را تغییر می دهد یا خیر. ما با یافتن صفرهای تابع مشتق دوم شروع می کنیم، زیرا فقط در این نقاط است که علامت مشتق دوم واقعاً می تواند تغییر کند. برای این کار معادله را حل می کنیم:
60 x 3 - 30 x = 0
ما می توانیم بلافاصله عبارت 30 x را فاکتور کنیم :
30 x (2 x 2 - 1) = 0
این مقادیر ممکن را برای x از 0.707-، 0 و 0.707 به ما می دهد . مشتق دوم مقدار صفر را در x = 0 برمی گرداند ، به این معنی که مطمئناً می تواند علامت متفاوتی در هر دو طرف این نقطه داشته باشد، اما آیا اینطور است؟ ما می توانیم با انتخاب مقادیر مناسب x در سمت چپ و راست x = 0 و وصل کردن آنها به تابع مشتق دوم، متوجه شویم . ما از مقادیر منهای صفر-نقطه-پنج و صفر-نقطه-پنج استفاده خواهیم کرد . این نتایج زیر را به ما خواهد داد:
ƒ′′(-0.5) = (60)(-0.5 3 ) - (30)(-0.5) = -7.5 + 15 = 7.5
ƒ′′(0.5) = (60)(0.5 3 ) - (30)(0.5) = 7.5 - 15 = -7.5
بنابراین مشتق دوم واقعاً علامت را در x = 0 تغییر می دهد و بنابراین باید یک نقطه عطف باشد. آزمایش مقادیر بازگردانده شده توسط مشتق دوم به دو طرف هر یک از دو نقطه بحرانی دیگر، تأیید می کند که آنها نیز با نقاط عطف در نمودار تابع اصلی مطابقت دارند. شما می توانید روابط بین نمودار تابع ƒ( x ) = 3 x 5 - 5 x 3 + 3 و روابط مشتقات اول و دوم آن را در تصویر زیر مشاهده کنید.
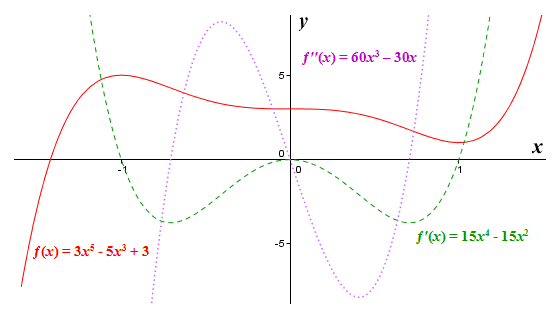
نمودارهای ƒ( x ) = 3 x 5 - 5 x 3 + 3 ، ƒ′( x ) = 15 x 4 - 15 x 2 ، و ƒ′′(x) = 60 x 3 – 30 x
منبع
https://www.technologyuk.net/mathematics/differential-calculus/second-derivative-test.shtml



























 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.