جهان در حال حاضر حدود ۹۰ میلیارد سال نوری قطر دارد. این بدان معناست که اگر از یک طرف فرضی جهان به فرض این که قابلیت فکر کردن دارد، سیگنالی با سرعت نور به طرف مقابل ارسال شود، ۹۰ میلیارد سال طول می‌کشد تا به مقصد برسد. آیا میدانید قطرجهان در حال حاضر حدود جهان چندکیلومتر است؟ مساحت و حجم آن چندکیلومتر مربع و چندکیلومتر مکعب است

نحوه محاسبه قبض برق

برق در دنیای امروز بسیار مهم است. به تلویزیون‌ها، رایانه‌ها، دستگاه‌های تهویه مطبوع، تلفن‌های همراه و ماشین‌های لباسشویی ما فقط به چند مورد اشاره می‌کند.

قبض برق قبض پولی است که برای برق مصرف شده بدهکار است.

فرمول محاسبه قبض برق

برای محاسبه قبض برق خود، باید میزان مصرف انرژی هر یک از لوازم خانگی و وسایل الکترونیکی خانه خود را محاسبه کنید.

• پس از مشخص کردن میزان مصرف انرژی هر دستگاه، وات دستگاه را در تعداد ساعات استفاده از دستگاه در روز ضرب کنید.
• تقسیم بر 1000 برای تبدیل وات به کیلووات.
• در نرخ کیلووات ساعت (کیلووات ساعت) خود ضرب کنید.

مثال:

یک دانش آموز در خانه اش فقط دو وسیله برقی دارد، یک تلویزیون و یک کتری برقی. او هر روز 5 ساعت تلویزیون تماشا می کند، 150 وات ساعت در روز مصرف می کند. او هر روز 1 ساعت از کتری برقی استفاده می کند و 100 وات ساعت در روز مصرف می کند. نرخ برق او 10 سنت در هر کیلووات ساعت تعیین قبض برق دانش آموزان برای یک ماه.

ما با قبض برق تلویزیون شروع می کنیم.

سپس قبض کتری برقی را محاسبه می کنیم.

در نهایت صورتحساب ها را اضافه می کنیم تا کل قبض برق به دست آید.

بنابراین، قبض برق او در آن ماه 3.06 دلار بود.

توسط جیم لوکاس مشارکت های اشلی هامر منتشر شده است 19 روز پیش

قانون صفر ترمودینامیک بیان می کند که اگر دو جسم هر کدام با جسم سوم در تعادل حرارتی باشند، با یکدیگر نیز در تعادل هستند.

قانون صفر ترمودینامیک (اعتبار تصویر: تیم شارپ)

قانون صفر ترمودینامیک بیان می کند که اگر دو جسم هر کدام با جسم سومی در تعادل حرارتی باشند، آنگاه با یکدیگر نیز در تعادل هستند. تعادل حرارتی به این معنی است که وقتی دو جسم با یکدیگر تماس پیدا می کنند و توسط مانعی که در برابر گرما نفوذ پذیر است از هم جدا می شوند، انتقال گرما از یکی به دیگری وجود نخواهد داشت.

به عبارت دیگر ، طبق گفته ناسا ، قانون صفر به این معنی است که هر سه جسم همگی در یک دما هستند . جیمز کلرک ماکسول این را شاید ساده‌تر بیان کرد وقتی گفت: "همه گرما از یک نوع هستند." (Longmans, Green, and Co. 1875). آنچه از همه مهمتر است این است که قانون صفر ثابت می کند که دما یک ویژگی اساسی و قابل اندازه گیری ماده است .

خلاصه

قانون کولن بیان می کند که نیروی الکترواستاتیک بین دو بار با حاصلضرب بارها نسبت مستقیم و با مجذور فاصله بین بارها نسبت معکوس دارد.

قانون کولن به صورت برداری در زیر آورده شده است.

طبق اصل برهم نهی، نیروی الکترواستاتیک خالص وارد بر یک بار برابر است با مجموع بردار نیروهای الکترواستاتیک منفرد وارد بر آن بار ناشی از هر بار دیگر سیستم بارها.

نیروی الکترواستاتیک بسیار بیشتر از نیروی گرانشی است.

تبدیل از یک سیستم اندازه گیری به سیستم دیگر

تبدیل طول، جرم، مساحت، حجم از یک سیستم اندازه گیری به سیستم اندازه گیری دیگر برای شناسایی واحدها بسیار مفید است. در مجموعه جداول زیر، واحدهای مختلف طول، مساحت، حجم، جرم از اندازه‌گیری استاندارد ایالات متحده تا سیستم اندازه‌گیری متریک را فهرست کرده‌ایم. لطفاً واحدهای مختلف تبدیل طول از اندازه‌گیری استاندارد ایالات متحده به سیستم اندازه‌گیری متریک را در زیر بیابید.

لطفاً در زیر واحدهای مختلف تبدیل جرم از اندازه‌گیری استاندارد ایالات متحده به سیستم اندازه‌گیری متریک را بیابید.

جدول زیر واحدهای مختلف تبدیل حجم از اندازه گیری استاندارد ایالات متحده به سیستم اندازه گیری متریک را نشان می دهد.

فیزیک دوچرخه موضوعی گسترده و پیچیده است، شاید بیش از آن چیزی که بتوان تصور کرد. اگرچه تعداد اجزای یک دوچرخه کم است، اما تعامل بین آنها و اصول دینامیکی درگیر، پیچیده است. این امر به ویژه در مورد پایداری دوچرخه، که نتیجه یک تعامل پویا پیچیده در سیستم دوچرخه سواری است، صادق است.

در این صفحه برخی از جنبه‌های اصلی فیزیک دوچرخه‌ها را توضیح خواهم داد، که باید به خواننده درک بیشتری از نحوه کار دوچرخه‌ها از منظر فیزیک بدهد.

فیزیک دوچرخه - پایداری

دوچرخه ها به طور ذاتی در هنگام سواری پایدار هستند. حتی دوچرخه های بدون سوار نیز اگر سرعت کافی به جلو داشته باشند، پایدار هستند. تلاش زیادی برای تجزیه و تحلیل عواملی که باعث پایداری دوچرخه می شوند انجام شده است. مشخص شده است که "مسیر" (در زیر نشان داده شده است) اغلب نقش مهمی در پایداری دوچرخه دارد. برای طراحی سنتی دوچرخه، اگر مسیر مثبت باشد، به این معنی که محور فرمان با زمین جلوتر از نقطه تماس چرخ جلو و زمین باشد، دوچرخه در هنگام سواری پایدارتر است (یعنی احتمال سقوط آن کمتر است. هنگام سوار شدن بر آن). اگر این برجستگی در پشت نقطه تماس (دنباله منفی) باشد، دوچرخه پایداری کمتری دارد و احتمال سقوط دوچرخه هنگام سوار شدن بر آن بیشتر است.



بر اساس پارامترهای هندسی نشان داده شده، فرمول ریاضی برای دنباله:



که در آن R W شعاع چرخ است، ساعت زاویه سر است که به عنوان نشان داده شده است، و ای اف با چنگک جمع کردن است، به عنوان نشان داده شده است، همچنین به عنوان چنگال جبران شناخته شده است.

هنگام تجزیه و تحلیل پایداری دوچرخه، استفاده از دو پارامتر رایج است. زاویه انحراف و زاویه فرمان دوچرخه. زاویه انحراف، زاویه چپ و راست قاب دوچرخه با صفحه عمودی است، و زاویه فرمان، زاویه ای است که چرخ جلو با صفحه دوچرخه (شامل قاب دوچرخه) ایجاد می کند. شکل زیر زاویه انحراف و فرمان را نشان می دهد.



که در آن θ زاویه ناب و α زاویه فرمان است. قرارداد علامت برای این زوایا معمولاً به شرح زیر است و با توجه به سواری که روی دوچرخه نشسته است: سمت راست θ مثبت و چپ چپ منفی θ است . فرمان راست α مثبت و فرمان چپ α منفی است. برای تجزیه و تحلیل پایداری، هر دوی این زوایا تنها متغیرهای مستقل مورد نیاز برای تجزیه و تحلیل ریاضی پایداری دوچرخه هستند. آنها به طور کامل جهت دوچرخه را در هنگام حرکت در جهت جلو توصیف می کنند. برای اینکه یک دوچرخه ثابت باشد، زاویه فرمان و لجن باید تمایل به خاموش شدن داشته باشند، به این معنی که این زوایا در اطراف صفر با مقادیر مثبت و منفی کوچک نوسان می کنند. این به نوبه خود به این معنی است که دوچرخه تمایل دارد با چرخش کمی عمودی بماند، در حالی که در جهت جلو حرکت می کند. جالب است که قفل کردن فرمان جلو همیشه باعث سقوط دوچرخه می شود. فیزیک پایداری مستلزم آن است که چرخ جلو بتواند آزادانه هدایت کند.

همانطور که گفته شد، تجزیه و تحلیل پایداری دوچرخه یک کار پیچیده است که شامل معادلات بزرگ و "درهم" است. فعل و انفعالات فیزیکی زیادی بین اجزای مختلف دوچرخه (یعنی چرخ جلو و عقب، ستون فرمان و قاب دوچرخه) وجود دارد که امکان توضیح کاملاً شهودی را فراهم می کند. برای به دست آوردن درک قابل توجهی از پایداری دوچرخه، بهتر است یک تحلیل دینامیک کامل انجام دهید و سپس درک خود را بر اساس نتایج این تجزیه و تحلیل قرار دهید.

تجزیه و تحلیل پایداری دوچرخه با استفاده از یک فرض "بی سوار" معمول است. این بدان معناست که دوچرخه فقط با دوچرخه به تنهایی (بدون سوار) مدل شده است. این امر تجزیه و تحلیل را بسیار ساده می کند، و در نتیجه اغلب فرض می شود که یک دوچرخه ثابت بدون سوار با حضور یک سوار نیز پایدار خواهد بود. این می تواند یک فرض معقول باشد اما متأسفانه "ورودی" راکب را نادیده می گیرد که بر پایداری دوچرخه در طول استفاده نیز تأثیر می گذارد.

با این وجود، در غیاب چیزی بهتر، انجام آنالیزهای پایداری روی دوچرخه‌های بدون سوار معمول است. اگر می‌خواهید تحلیل کامل دوچرخه‌های بدون سوار را ببینید، مقاله زیر را ببینید:

معادلات دینامیک خطی برای تعادل و هدایت دوچرخه: یک معیار و بررسی, JP Meijaard, Jim M. Papadopoulos, Andy Ruina, AL Schwab, ژوئن 2007.

اثرات ژیروسکوپی بر پایداری دوچرخه

باور رایج این است که اثرات ژیروسکوپی به خودی خود چیزی است که دوچرخه را پایدار می کند. این در واقع اینطور نیست. اگرچه جلوه‌های ژیروسکوپی نقشی را ایفا می‌کنند، اما صرفاً بخشی از یک تعامل دینامیکی بسیار بزرگ‌تر هستند که بین اجزای مختلف دوچرخه اتفاق می‌افتد، که در مجموع همان چیزی است که در نهایت دوچرخه را در حین دوچرخه‌سواری پایدار می‌کند. طراحی یک دوچرخه، و پیکربندی اجزای مختلف، در طول اعصار (عمدتاً از طریق آزمون و خطا) بهینه شده است تا آن را تا حد امکان پایدار کند.

همانطور که گفته شد، جلوه های ژیروسکوپی سهم اصلی در پایداری دوچرخه نیست، اما هنوز هم آموزنده است که ببینید چگونهاثرات ژیروسکوپی به پایداری کمک می کند. برای درک این سهم، سناریوی زیر را در نظر بگیرید:

فرض کنید یک دوچرخه بدون سوار با سرعت خاصی حرکت می کند. بیایید بیشتر بگوییم که دوچرخه به سمت راست خم می شود ( θ مثبت ). این باعث می شود چرخ جلو به راست هدایت شود ( α مثبت) به دلیل اثر ژیروسکوپی. برای کمک به درک اینکه چرا این اتفاق می‌افتد، به این فکر کنید که برای جلوگیری از فرمان‌پذیری چرخ جلو به سمت راست چه باید کرد. برای جلوگیری از هدایت چرخ جلو به سمت راست، باید گشتاوری را در جهت چپ (برعکس) روی فرمان اعمال کنید. بنابراین، با نبود گشتاور (در دوچرخه بدون سوار)، چرخ جلو به طور طبیعی به سمت راست هدایت می شود. شما می توانید این را خودتان با دوچرخه امتحان کنید. دوچرخه را از روی زمین بلند کنید و به سرعت چرخ جلو را در جهت جلو بچرخانید. سپس، قاب دوچرخه را کمی به چپ یا راست متمایل کنید و ببینید در پاسخ چه اتفاقی برای چرخ جلو می افتد. این را با اتفاقی که هنگام چرخاندن چرخ جلو، هنگام کج کردن دوچرخه روی می‌دهد، مقایسه کنید.

با چرخاندن فرمان به سمت راست، دوچرخه در یک مسیر دایره ای (به سمت راست) حرکت می کند. این باعث کاهش θ می شودبه دلیل تأثیر شتاب مرکزگرا. این به نوبه خود باعث می شود دوچرخه به سمت چپ خم شود ( θ منفی ) که باعث می شود چرخ جلو به سمت چپ هدایت شود ( α منفی )، که سپس باعث می شود دوچرخه در یک مسیر دایره ای (به سمت چپ) حرکت کند. شتاب گریز از مرکز این باعث کاهش θ (دوچرخه به سمت راست می شود) می شود که دوباره باعث می شود چرخ جلو به راست هدایت شود و روشن و روشن شود. اگر دوچرخه در ابتدا به چپ خم شود، زنجیره‌ای از رویدادها اتفاق می‌افتد ( θ منفی ). این زنجیره رویدادها از سقوط دوچرخه جلوگیری می کند.

کل فعل و انفعالات فیزیکی در حال وقوع در واقع پیچیده تر از سناریوی بالا هستند، به خصوص به دلیل نوسانات θ و α.. اما سناریوی ساده‌شده‌ای که در بالا ارائه شد، نقش تأثیرگذاری ژیروسکوپی را در پایدار نگه داشتن دوچرخه نشان می‌دهد.

Leaning Into A Turn



منبع: http://en.wikipedia.org/wiki/Bicycle_and_motorcycle_dynamics. نویسنده: http://en.wikipedia.org/wiki/User:Furmanj

هنگام دوچرخه سواری، برای جبران اثر شتاب مرکزگرا، باید به یک پیچ خم شوید. انحراف به سمت داخل شتاب مرکزگرا را متعادل می کند که چرخش را بدون افتادن ممکن می کند.

برای تجزیه و تحلیل فیزیک پشت ناب، شماتیک زیر را در نظر بگیرید.



جایی که:

θ زاویه ناب است

R شعاع پیچ اندازه گیری شده از مرکز جرم G سیستم دوچرخه سواری است.

ج است شتاب مرکزگرا از مرکز جرم G از سیستم دوچرخه سوار

متر است که جمعی از سیستم دوچرخه سوار

گرم شتاب به دلیل گرانش، بر روی زمین، که 9.8 متر است / s را 2

L فاصله است از نقطه G به نقطه تماس موثر P بین دوچرخه و زمین

N نیروی نرمال بین دوچرخه و زمین است

F نیروی اصطکاک بین دوچرخه و زمین است، در جهت ج از آنجا که هیچ شتاب در جهت عمودی مجموع وجود دارد نیروهای عمودی صفر است. بدین ترتیب،






قانون دوم نیوتن را در جهت افقی اعمال کنید:



که در آن v سرعت دوچرخه در اطراف پیچ است.

لحظه های مربوط به نقطه G را جمع کنید :



(توجه داشته باشید که اثرات سه بعدی را در این معادله نادیده می گیریم. آنها ناچیز فرض می شوند).

سه معادله بالا را با هم ترکیب کنید تا یک عبارت برای زاویه θ لاغر پیدا کنید . ما



در بخش بعدی ما در نیروها و قدرت.

نیروها و نیرو

در شکل زیر دوچرخه ای را نشان می دهد که در سربالایی با زاویه شیب Φ و با سرعت V حرکت می کند .



برای به حرکت درآوردن دوچرخه در سربالایی، دوچرخه سوار باید پدال ها را فشار دهد. پدال‌ها 180 درجه جابجا شده‌اند، به این معنی که تنها یک پدال را می‌توان در یک زمان، از موقعیت بالا به پایین، و سپس به پدال دیگر سوئیچ کرد.

با توجه به نیروی F 1 که بر روی پدال وارد می شود، می توانیم نیروی حاصل از F 4 را بین چرخ عقب و زمین محاسبه کنیم. این نیرویی است که دوچرخه را به جلو می راند.

بر اساس این فرض که شتاب (خطی و زاویه ای) ناچیز است، می توانیم تحلیل گشتاور را با دقت خوبی انجام دهیم. از این رو، می توانیم این را به عنوان یک مشکل ثابت در نظر بگیریم.

شکل زیر را با نیروها و ابعاد شعاعی در نظر بگیرید.



کجا:

F 1نیروی اعمال شده به پدال است

R 1 شعاع پدال است

F 2 نیروی وارد بر میل لنگ اصلی، با توجه به زنجیره مخاطب

R 2 است میل لنگ شعاع اصلی

F 3 نیروی وارد بر دنده عقب است، به علت تماس های زنجیره ای

R 3 شعاع چرخ دنده عقب است

F 4 نیرویی است که بر چرخ عقب در اثر تماس با زمین وارد می شود. توجه داشته باشید که ضریب اصطکاک استاتیکی بین چرخ و زمین باید به اندازه کافی بزرگ برای حمایت از این نیروی شود، در غیر این صورت لغزش رخ می دهد

R 4 شعاع چرخ عقب است


با استفاده از فرض تعادل ایستا، می‌توانیم معادلات گشتاور زیر را بنویسیم:



و



از آنجایی که F 2 = F 3 ، می‌توانیم دو معادله بالا را ترکیب کنیم تا بیانی برای F 4 بدست آوریم :



نیروی F 4 چیزی است که دوچرخه را به جلو می‌برد. اگر فرض کنیم دوچرخه با سرعت ثابت (بدون شتاب) حرکت می کند، نیروی F 4 باید با نیروهای مقاومت مخالف حرکت دوچرخه برابر باشد. این نیروهای مقاوم عبارتند از: جاذبه، مقاومت غلتشی، کشش هوا و اصطکاک داخلی دوچرخه. اگر از دومی غافل شویم، می‌توانیم عبارت ریاضی زیر را بنویسیم:



کجا:

Fنیرویی است که دوچرخه را به جلو می راند. توجه داشته باشید که F ≡ F 4

C r ضریب مقاومت غلتشی است که می تواند 0.0022 تا 0.005 برای لاستیک دوچرخه باشد (رجوع کنید: http://en.wikipedia.org/wiki/Rolling_resistance)

C d ضریب درگ

ρ است. چگالی هوایی که دوچرخه از طریق آن حرکت می کند

A سطح مقطع پیش بینی شده دوچرخه + راکب عمود بر جهت جریان (یعنی عمود بر v ) است و v سرعت دوچرخه نسبت به هوا است.


اولین عبارت در سمت راست معادله فوق سهم گرانش است. اصطلاح دوم سهم مقاومت غلتشی است. سومین عبارت سهم کشش هوایی است.

برای ارزیابی توان P مورد نیاز برای به حرکت درآوردن دوچرخه، معادله فوق را در v ضرب کنید . ما P = پارامتر Fv ، و



برای یک سطح صاف (بدون شیب) مجموعه Φ = 0. ما



و




ما همچنین می توانید برای سرعت حد یک دوچرخه در سرازیری به پایین تپه با زاویه تمایل داده شده از حل Φ . از آنجایی که سوارکار در این حالت هیچ نیرویی به پدال ها وارد نمی کند، F ≡ F 4 داریم.= 0. بنابراین، نیروی گرانش باید نیروهای مقاومتی ناشی از مقاومت غلتشی و کشش هوا را متعادل کند. از این رو، می‌توانیم سرعت کوستینگ پایانی v را در معادله زیر حل کنیم:




طبیعتاً، هنگام دوچرخه‌سواری می‌خواهیم نیروهای مقاومتی مخالف حرکت را تا حد امکان پایین نگه داریم. این امر با تحت فشار قرار دادن لاستیک ها (که مقاومت غلتشی را به حداقل می رساند) و کوچک نگه داشتن ناحیه جلویی A تا حد امکان برای کاهش کشش هوا انجام می شود، به خصوص هنگام سفر با سرعت بالا، مانند مسابقه. به طور معمول، مقاومت غلتشی بسیار بالاتر از کشش هوا است، بنابراین کاهش A برای سوارکاری معمولی که با سرعت متوسط ​​حرکت می کند مهم نیست.

یک آزمایش سرگرم کننده

این آزمایش جالب مربوط به فیزیک دوچرخه را امتحان کنید (در زیر نشان داده شده است). دوچرخه را به صورت عمودی بایستید و یکی از پدال ها را طوری جهت دهید که در پایین قرار گیرد. بعد، پدال را به چپ فشار دهید. دوچرخه به کدام سمت حرکت می کند؟



پاسخ: دوچرخه به سمت چپ حرکت می کند (که ممکن است برای شما غیر شهودی باشد). حتی اگر نیرویی که به پدال وارد می‌کنید، میل لنگ اصلی را در جهت عقربه‌های ساعت می‌چرخاند، که جهت مورد نیاز برای حرکت دوچرخه به سمت راست است، دوچرخه در نهایت به سمت چپ حرکت می‌کند. این به این دلیل است که نیروی خارجی F 1 که به دوچرخه وارد می کنید، منجر به نیروی کمتری F 4 در جهت مخالف می شود. از F 1 > F 4، دوچرخه به سمت چپ حرکت می کند. حال، اگر بخواهید روی دوچرخه بنشینید و با پای خود نیروی F 1 را اعمال کنید، دوچرخه به سمت راست حرکت می کند زیرا F 1 اکنون یک نیروی داخلی در سیستم دوچرخه سوار است و بنابراین تنها نیروی خارجی است که بر روی دوچرخه وارد می شود. دوچرخه F 4 است که روی چرخ عقب عمل می کند و دوچرخه را به سمت راست هل می دهد.

منبع

https://www.real-world-physics-problems.com/bicycle-physics.html

سقوط آزاد به حرکت هر جسمی که فقط تحت نیروی جاذبه باشد اطلاق می گردد.

اسکات در حال اجرای آزمایشی از سقوط آزاد در ماه و در طی پروژه آپولو ۱۵.

محتویات

• ۱سقوط آزاد در مکانیک نیوتونی
  • ۱.۱بدون وجود اصطکاک
  • ۱.۲با وجود اصطکاک
• ۲منابع

سقوط آزاد در مکانیک نیوتونی[ویرایش]

بدون وجود اصطکاک[ویرایش]

تنها نیروی وارد بر جسم هنگام سقوط، نیروی وزن آن یا  است و طبق قانون دوم نیوتون شتاب وارد بر جسم رو به پایین و برابر با  خواهد بود که به نام شتاب گرانشی شناخته می‌شود. با انتگرال از معادله شتاب-زمان به معادله سرعت-زمان می‌رسیم:

که در آن داریم:

 زمان

 سرعت در راستای عمود در زمان 

 سرعت اولیه جسم است در زمان ۰.

با انتگرال دوم از معادله سرعت-زمان به معادله مکان-زمان خواهیم رسید:

که در آن داریم:

 مکان جسم نسبت به مبدا در زمان 

 مکان اولیه جسم نسبت به مبدا در زمان ۰.

با وجود اصطکاک

با وجود اصطکاک دو نیروی مخالف هم به جسم وارد می‌شوند اولی گرانش و دیگری اصطکاک. نیروی گرانش ثابت و برابر  رو به پایین است ولی نیروی اصطکاک متغیر و وابسته به سرعت جسم و رو به بالاست و برابر:

که در آن:

 نیروی اصطکاک

 ثابتی که به جنس گاز و مساحت جسم بستگی دارد

 سرعت جسم در راستای عمود است.

بنابرین برآیند نیروها برابر است با:

پس اندازه شتاب در راستای عمود برابر است با:

 این معادله تبدیل به یک معادله دیفرانسیل مرتبه اول می‌شود که با حل آن سرعت به صورت زیر بدست می‌آید:

که در آن  سرعت حدی نام دارد.

میدان جاذبه یکنواخت با مقاومت هوا [ ویرایش ]

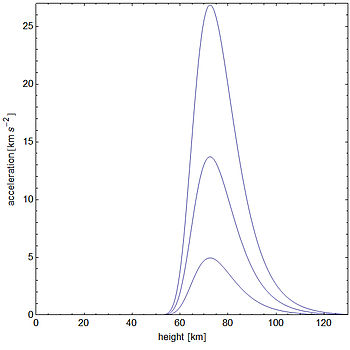
شتاب یک شهاب سنگ کوچک هنگام ورود به جو زمین با سرعتهای مختلف مختلف.

این مورد ، که مربوط به چتربازان ، چتربازان یا هر جرم دیگری است ، ، و سطح مقطع ، ، با تعداد رینولدز بسیار بالاتر از عدد بحرانی رینولدز ، بنابراین مقاومت هوا متناسب با مربع سرعت سقوط است ،، دارای یک معادله حرکت است

جایی که است چگالی هوا واست ضریب درگ ، تصور می شود ثابت هر چند به طور کلی آن را بر روی عدد رینولدز بستگی دارد.

با فرض سقوط جسمی از حالت استراحت و عدم تغییر چگالی هوا با ارتفاع ، راه حل این است:

که در آن سرعت ترمینال توسط داده می شود

سرعت جسم در برابر زمان می تواند با گذشت زمان ادغام شود و موقعیت عمودی را به عنوان تابعی از زمان پیدا کند:

با استفاده از رقم 56 متر بر ثانیه برای سرعت نهایی انسان ، متوجه می شویم که پس از 10 ثانیه 348 متر سقوط کرده و 94٪ سرعت ترمینال را بدست خواهد آورد و پس از 12 ثانیه 455 متر سقوط خواهد کرد و به دست خواهد آمد 97٪ سرعت ترمینال. با این حال ، وقتی تراکم هوا ثابت نباشد ، مثلاً برای اجسامی که از ارتفاع بالا می افتند ، حل معادله حرکت بسیار دشوارتر می شود و شبیه سازی عددی حرکت معمولاً لازم است. این شکل نیروهایی را نشان می دهد که بر روی شهاب سنگ ها در جو بالایی زمین وارد می شوند. پرش های HALO ، از جمله پرش های رکوردی جو کیتینگر و فلیکس باومگارتنر ، نیز در این گروه قرار دارند. [5]

میدان جاذبه قانون مربع معکوس [ ویرایش ]

می توان گفت که دو جسم در فضا در حال فقدان یکدیگر در غیاب نیروهای دیگر در حال سقوط آزاد به دور یکدیگر هستند ، به عنوان مثال ماه یا یک ماهواره مصنوعی "به دور زمین" می افتد ، یا یک سیاره "به دور خورشید می افتد" . فرض بر این است که اشیا means کروی به معنای این است که معادله حرکت توسط قانون جاذبه جهانی نیوتن اداره می شود ، با راه حل هایی برای مسئله گرانشی دو بدن ، مدارهای بیضوی هستند و از قوانین حرکت سیاره کپلر پیروی می کنند . این ارتباط بین سقوط اجسام نزدیک به زمین و اجرام در مدار به بهترین شکل با آزمایش فکری ، گلوله توپ نیوتن نشان داده می شود .

حرکت دو جسم در حال حرکت شعاعی نسبت به یکدیگر با حرکت زاویه ای را می توان یک حالت خاصی از یک مدار بیضی شکل از خروج از مرکز الکترونیکی = 1 ( مسیر بیضوی شعاعی ). این به شما امکان می دهد زمان سقوط آزاد را برای دو جسم نقطه ای در یک مسیر شعاعی محاسبه کند. حل این معادله حرکت به عنوان تابعی از تفکیک زمان را به همراه دارد:

جایی که

 زمان پس از شروع پاییز است

 فاصله بین مراکز بدن است

 مقدار اولیه است 

است پارامتر گرانشی استاندارد .

جایگزین کردنما زمان سقوط آزاد را دریافت می کنیم .

جدایی به عنوان تابعی از زمان با معکوس معادله داده می شود. وارون دقیقاً با سری قدرت تحلیلی نشان داده می شود:

ارزیابی این بازده: [6] [7]

جایی که

اونس (مخفف: oz) از واحدهای جرم است. Oz سرواژه عبارت ounce است.

واحد اونس در دستگاه‌های گوناگون همچون یکاهای انگلیسی، یکاهای سلطنتی و دستگاه یکاهای معمول ایالات متحده کاربرد داشته است. و در هر یک از این دستگاه‌ها وزن متفاوتی دارد. اونس معمولی در سیستم بین‌المللی اوزان برابر با یک‌شانزدهم پوند یا ۴۰۰ ارزن است که در سیستم متریک مساوی ۲۸٫۳۴۹۵۲۳۱۲۵ گرم می‌شود. این واحد در ایالات متحده بسیار متداول است، در بریتانیا استفاده رسمی از آن در سال ۲۰۰۰ به پایان رسید اما هنوز هم در این کشور استفاده می‌شود.

همچنین برای اندازه‌گیری وزن فلزات گرانبها یعنی؛ طلا، نقره، پلاتین و پالادیم از اونس بین‌المللی تروا استفاده می گردد که معادل ۳۱٫۱۰۳۴۷۶۸ گرم می باشد. این اونس فقط برای اندازه‌گیری این فلزات گران‌بها کاربرد دارد و وزن شمش‌ها و سکه‌های طلا و دیگر فلزات گران‌بها و همینطور قیمت آن‌ها معمولاً با اونس تروا بیان می‌شود. اصطلاح یک اونس طلا به معنی طلایی یک‌تکه یا ساچمه با وزن یک اونس تروا و با خلوص ۹۹٫۹۹ درصد (۲۴ عیار) است.

انواع دیگر اونس شامل اونس ماریا ترزا معادل ۲۸٫۰۶۶۸ گرم، اونس اسپانیایی معادل ۲۸٫۷۵ گرم، اونس متریک چینی معادل ۵۰ گرم و اونس متریک هلندی معادل ۱۰۰ گرم، می‌شوند.