ابزارک درون سنجی فرمول های حاصل به جمع تصویر

محدب و مقعر کلماتی هستند که برای توصیف شکل یا انحنای یک منحنی استفاده می کنیم. از طبقه‌بندی نقاط ثابت (به صفحه نقاط ثابت مراجعه کنید ) به یاد بیاورید که می‌توانیم مشتق دوم یک تابع را با دوبار افتراق پیدا کنیم. ما همچنین به مشتق دوم نیاز داریم تا ببینیم آیا یک تابع در یک نقطه خاص مقعر یا محدب است. نقطه عطف جایی است که یک منحنی از مقعر به محدب یا بالعکس تغییر می کند.

توابع محدب و مقعر

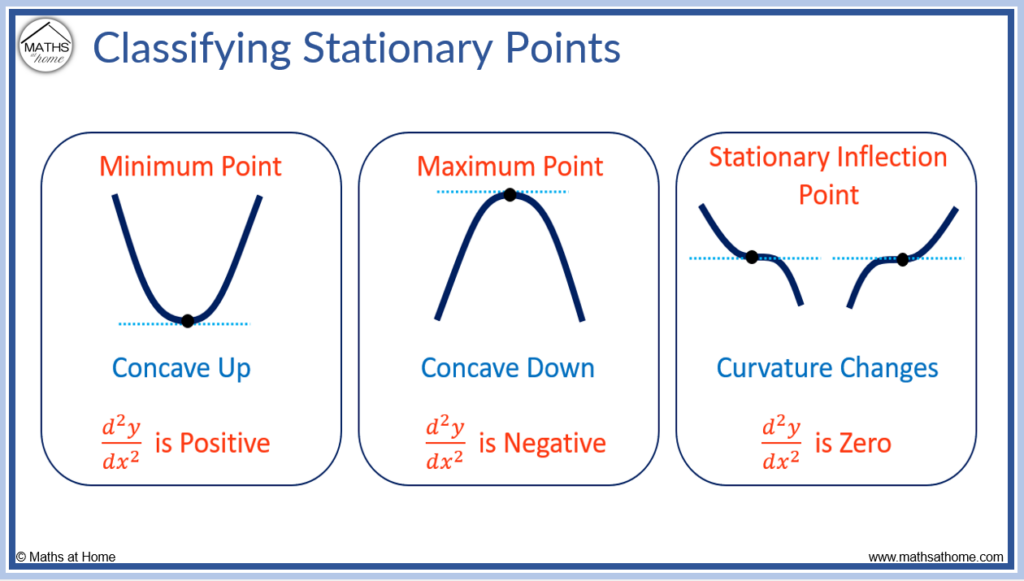
باگر در هر نقطه از منحنی، مشتق دوم منفی باشد، می گوییم منحنی در آن نقطه مقعر است. برعکس، اگر مشتق دوم در هر نقطه مثبت باشد، می گوییم که منحنی در آن نقطه محدب است. نتیجه این است که یک فاصله حول یک ماکزیمم مقعر و یک فاصله حول یک حداقل محدب وجود دارد. به مثال 1 مراجعه کنید. نقطه ای که در آن یک منحنی از مقعر به محدب یا بالعکس تغییر می کند به عنوان نقطه عطف شناخته می شود. در هر نقطه از یک منحنی، نه لزوما نقاط ثابت. اگر در هر نقطه از یک منحنی، مشتق دوم منفی باشد، می گوییم که منحنی مقعر است

نمودار y=x^2 را در نظر بگیرید. مشتق 2x است و بنابراین مشتق دوم این تابع همیشه مثبت است و بنابراین منحنی همیشه محدب است.

نقاط عطف

نمودار y=x^3 را در نظر بگیرید. مشتق 3x^2 و مشتق دوم 6x است. مشتق دوم وقتی x=0 صفراست، وقتی x>0 مثبت است و وقتی x<0 منفی است. نتیجه این است که نقطه(0,0) یک نقطه عطف است.

نقاط ثابت چیست؟

نقاط ثابت نقاطی از تابعی هستند که مشتق آن برابر با صفر است. در این نقاط، مماس بر منحنی افقی است. نقاط ثابت به این دلیل نامیده می شوند که تابع در این نقاط نه افزایش یا کاهش می یابد. 3 نوع نقطه ثابت وجود دارد: حداکثر، حداقل و انحراف ثابت.

• نقطه حداکثر نقطه ایست که در آن منحنی مقعر (∩ شکل) است.
• نقطه حداقل نقطه ایست که در آن منحنی مقعر به سمت پایین (∪ شکل) است.
• نقطه عطف نقطه ای از منحنی است که در آن انحنا تغییر می کند و مماس در این نقطه افقی است.

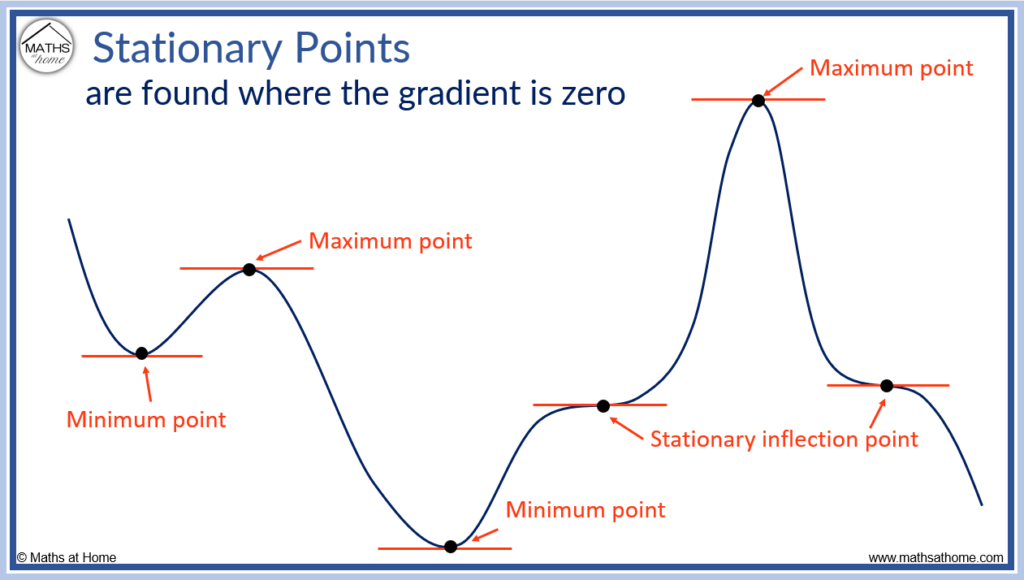
نقاط اکسترمم، نقاطی روی یک تابع هستند که در آنها می چرخد. یعنی نمودار از افزایش به کاهش یا بالعکس تغییر می کند. دو نوع نقطه اکسترمم وجود دارد: نقطه حداکثر که در آن تابع از افزایش به کاهش تغییر می کند، یا نقطه حداقل که در آن تابع از کاهش به افزایش تغییر می کند.

از قاعده تقسیم استفاده می کنیم

این سوال مفهوم قانون زنجیره را در بر خواهد گرفت.