x + 1/x = 2
دو طرف را در x ضرب می کنیم:
=> x^ 2 + 1 = 2x
=> x ^2 – 2x + 1 = 0
با اتحاد مربع تجزیه می کنیم:
=> (x – 1)^ 2 = 0
=> x – 1 = 0
=> x = 1
x + 1/x = 2
دو طرف را در x ضرب می کنیم:
=> x^ 2 + 1 = 2x
=> x ^2 – 2x + 1 = 0
با اتحاد مربع تجزیه می کنیم:
=> (x – 1)^ 2 = 0
=> x – 1 = 0
=> x = 1
x+1/x=2 و x(1/x)=1 ===> S=2 ,P=1===>
x=1 ===>
x^100 +1/x^100=1+1=2
برای شمارش تعداد عناصر در اجتماع دو مجموعه (A و B)، باید تعداد آیتم های مجموعه A، تعداد آیتم های مجموعه B و تعداد آیتم های هر دو A و B را بدانیم. (اشتراک الف و ب).
صرف جمع کردن عناصر A و B با یکدیگر، عناصر موجود در اشتراک را دو بار میشماریم، بنابراین برای بدست آوردن تعداد صحیح عناصر در اجتماع A و B، باید محل اشتراک A و B را کم کنیم. با استفاده از فرمول ریاضی زیر بیان شده است:

راه دیگر برای نگاه کردن به این مفهوم استفاده از نمودار ون یا نمایش بصری مجموعه ها است. در شکل 1 زیر، دایره سمت چپ نشان دهنده مجموعه A، دایره سمت راست مجموعه B، و همپوشانی نشان دهنده اشتراک A و B است. هر چیزی که در هر دو دایره باشد نشان دهنده اجتماع A و B است. هر دو دایره، باید کم شود تا فقط یک بار شمارش شود. توجه داشته باشید که جهان U شامل همه چیز در کل جعبه است.
شکل 1: نمودار ون با دو مجموعه

برای باز کردن قفل این درس باید عضو Study.com باشید. حساب کاربری برای خود بسازید
اکنون که با دو مجموعه تمرین کرده ایم، بیایید نحوه شمارش عناصر شامل سه مجموعه (A، B و C) را در نظر بگیریم. اگر تعداد عناصر هر یک از سه مجموعه را اضافه کنیم، دوباره عناصری را که در بیش از یک مجموعه قرار دارند، چندین بار می شماریم، همانطور که در شکل 2 زیر نشان داده شده است. مناطقی که دو مجموعه با هم تداخل دارند دو بار و منطقه ای که هر سه مجموعه با هم همپوشانی دارند سه بار شمارش می شود.
شکل 2: نمودار ون با سه مجموعه و تعداد منطقه

اگر هر یک از جفتها را کم کنیم، فرمول به شکل زیر است:

مشکل این روش این است که ناحیه وسطی که هر سه مجموعه در آن تلاقی می کنند به هیچ وجه شمارش نمی شود. این در شکل 3 نشان داده شده است.
شکل 3: نمودار ون با سه مجموعه و تعداد منطقه تنظیم شده است
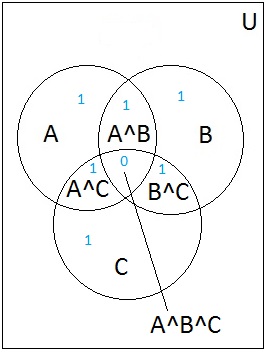
برای رفع این مشکل، به سادگی میتوانیم اشتراک هر سه مجموعه را دوباره به داخل اضافه کنیم، به طوری که فرمول اکنون به شکل زیر در میآید:
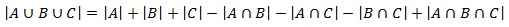
اصل شمول و عدم شمول را می توان به هر تعداد مجموعه n تعمیم داد ، که در آن n یک عدد صحیح مثبت است. اصل کلی شمول و عدم شمول به شرح زیر تعریف می شود:
بگذارید A 1 , A 2 , …, A n مجموعه های متناهی باشند. سپس

به عنوان مثال، اعمال این فرمول برای چهار مجموعه نتیجه می دهد:

این درس اصل
برای شمارش تعداد عناصر در اجتماع دو مجموعه (A و B)، باید تعداد آیتم های مجموعه A، تعداد آیتم های مجموعه B و تعداد آیتم های هر دو A و B را بدانیم. (اشتراک الف و ب).
صرف جمع کردن عناصر A و B با یکدیگر، عناصر موجود در اشتراک را دو بار میشماریم، بنابراین برای بدست آوردن تعداد صحیح عناصر در اجتماع A و B، باید محل اشتراک A و B را کم کنیم. با استفاده از فرمول ریاضی زیر بیان شده است:

راه دیگر برای نگاه کردن به این مفهوم استفاده از نمودار ون یا نمایش بصری مجموعه ها است. در شکل 1 زیر، دایره سمت چپ نشان دهنده مجموعه A، دایره سمت راست مجموعه B، و همپوشانی نشان دهنده اشتراک A و B است. هر چیزی که در هر دو دایره باشد نشان دهنده اجتماع A و B است. هر دو دایره، باید کم شود تا فقط یک بار شمارش شود. توجه داشته باشید که جهان U شامل همه چیز در کل جعبه است.
شکل 1: نمودار ون با دو مجموعه

برای باز کردن قفل این درس باید عضو Study.com باشید. حساب کاربری برای خود بسازید
اکنون که با دو مجموعه تمرین کرده ایم، بیایید نحوه شمارش عناصر شامل سه مجموعه (A، B و C) را در نظر بگیریم. اگر تعداد عناصر هر یک از سه مجموعه را اضافه کنیم، دوباره عناصری را که در بیش از یک مجموعه قرار دارند، چندین بار می شماریم، همانطور که در شکل 2 زیر نشان داده شده است. مناطقی که دو مجموعه با هم تداخل دارند دو بار و منطقه ای که هر سه مجموعه با هم همپوشانی دارند سه بار شمارش می شود.
شکل 2: نمودار ون با سه مجموعه و تعداد منطقه

اگر هر یک از جفتها را کم کنیم، فرمول به شکل زیر است:

مشکل این روش این است که ناحیه وسطی که هر سه مجموعه در آن تلاقی می کنند به هیچ وجه شمارش نمی شود. این در شکل 3 نشان داده شده است.
شکل 3: نمودار ون با سه مجموعه و تعداد منطقه تنظیم شده است

برای رفع این مشکل، به سادگی میتوانیم اشتراک هر سه مجموعه را دوباره به داخل اضافه کنیم، به طوری که فرمول اکنون به شکل زیر در میآید:
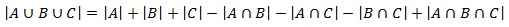
اصل شمول و عدم شمول را می توان به هر تعداد مجموعه n تعمیم داد ، که در آن n یک عدد صحیح مثبت است. اصل کلی شمول و عدم شمول به شرح زیر تعریف می شود:
بگذارید A 1 , A 2 , …, A n مجموعه های متناهی باشند. سپس

به عنوان مثال، اعمال این فرمول برای چهار مجموعه نتیجه می دهد:

این درس اصل گنجاندن-حذف را پوشش میدهد که میتوان از آن برای شمارش تعداد آیتمهای درون مجموعههایی که موارد مشترک دارند، استفاده کرد. ما با مفاهیم بنیادی تئوری مجموعهها ، از جمله اجتماع و اشتراک ، که برای حل مسائل شمارش با استفاده از اصل شمول - طرد ضروری هستند، شروع کردیم. سپس فرمولها و مثالهای هر کدام، از جمله نمونههای دو مجموعه و سه مجموعه را بررسی کردیم. در نهایت، ما یک فرمول کلی برای اصل گنجاندن-خروج اعمال شده برای n مجموعه ارائه کردیم.
را پوشش میدهد که میتوان از آن برای شمارش تعداد آیتمهای درون مجموعههایی که موارد مشترک دارند، استفاده کرد. ما با مفاهیم بنیادی تئوری مجموعهها ، از جمله اجتماع و اشتراک ، که برای حل مسائل شمارش با استفاده از اصل شمول - طرد ضروری هستند، شروع کردیم. سپس فرمولها و مثالهای هر کدام، از جمله نمونههای دو مجموعه و سه مجموعه را بررسی کردیم. در نهایت، ما یک فرمول کلی برای اصل گنجاندن-خروج اعمال شده برای n مجموعه ارائه کردیم.
بر: 21 نوامبر 2018
درک کامل اصل شمول-حذف در ریاضیات گسسته برای ایجاد یک پایه محکم در نظریه مجموعه ها حیاتی است.
با اصل گنجاندن-خروج، به طور کلی دو نوع سوال در برنامه های درسی ریاضیات گسسته مقدماتی و سطح پایین وجود دارد. این انواع سوالات عبارتند از:
در این مقاله، چندین مثال و راهحل اصل گنجاندن-خروج را برای هر دو نوع مورد بحث قرار خواهیم داد. نمودارهای ون، اگرچه ضروری نیستند، برای کمک به مفهوم سازی گنجانده شده اند.
از میان 50 بیمار بستری شده در بیمارستان، 25 نفر مبتلا به ذات الریه، 30 نفر مبتلا به برونشیت و 10 نفر با هر دو ذات الریه و برونشیت تشخیص داده شده اند. تعیین کنید:
الف) تعداد بیمارانی که پنومونی یا برونشیت (یا هر دو) تشخیص داده شده است.
(ب) تعداد بیمارانی که پنومونی یا برونشیت تشخیص داده نشده است.
اولین قدم شناسایی رسمی مجموعه ها و نشان دادن تعداد عناصر در هر یک است. این را می توان صرفاً با اطلاعات داده شده انجام داد. هیچ محاسبه ای لازم نیست. با این سوال اصل شمول-حذف، سه مجموعه را می توان به صورت زیر تعریف کرد:
اجازه دهید U کل مجموعه بیماران را نشان دهد. اجازه دهید P و B به ترتیب مجموعه بیمارانی را که پنومونی و برونشیت تشخیص داده اند نشان دهند. بدین ترتیب:
|U| = 50
|P| = 25
|B| = 30
|P ∩ B| = 10
اکنون ممکن است یک نمودار ون ایجاد کنیم. دو مجموعه و در نتیجه دو دایره وجود دارد. از آنجایی که تعداد عناصر موجود در تقاطع P و B را می دانیم ( |P ∩ B| ) ابتدا می توانیم این را پر کنیم:
اکنون می توانیم محاسبه کنیم که چند عنصر فقط در P زندگی می کنند اما نه |P ∩ B|:
از آنجایی که
|P| = 25 و |P ∩ B| = 10، 15
عنصر
(25-10 = 15)
منحصر به P وجود دارد.
برای محاسبه تعداد عناصری که فقط در B زندگی می کنند اما نه |P ∩ B| از همین روش استفاده کنید:
از آنجایی که
|B| = 30 و |P ∩ B| = 10، 20
عنصر
(30-10 = 20)
منحصر به B وجود دارد.
این اطلاعات جدید باید به شکل زیر به نمودار ون اضافه شود:
کار مقدماتی کامل است و ما اطلاعات کافی برای پاسخگویی مستقیم به سوالات داریم:
(الف) تعداد بیماران مبتلا به پنومونی یا برونشیت (یا هر دو) را تعیین کنید .
این همان درخواست برای تعیین |P ∪ B| است. با نگاهی به نمودار ون، پاسخ را به صورت زیر فرموله کنید:
|P ∪ B| = 15 + 10 + 20
= 45
بنابراین 45 بیمار مبتلا به پنومونی یا برونشیت تشخیص داده می شوند.
همین پاسخ را می توان با استفاده از اصل گنجاندن-استخراج مستقیماً بدون مراجعه به نمودار ون نیز بدست آورد:
|P ∪ B| = |P| + |B| – |P ∪ B|
= (25 + 30) - (10)
= 45
بنابراین 45 بیمار مبتلا به پنومونی یا برونشیت تشخیص داده می شوند.
(ب) تعداد بیمارانی که پنومونی یا برونشیت تشخیص داده نشده اند را تعیین کنید.
این همان درخواست برای تعیین |(P ∪ B)'| است. ما می دانیم که در مجموع 50 بیمار وجود دارد - از این تعداد 45 نفر مبتلا به پنومونی یا برونشیت هستند. از این برای حل این سوال استفاده کنید:
|U| = 50.
|P ∪ B| = 45
از این رو،
|(P ∪ B)'|
= 50 - 45 = 5
5 بیمار مبتلا به پنومونی یا برونشیت تشخیص داده نشده اند.
یک شرکت بزرگ توسعه نرم افزار 100 برنامه نویس کامپیوتر را استخدام می کند. از این تعداد 45 نفر به جاوا، 30 نفر به سی شارپ، 20 نفر به زبان پایتون، شش نفر به زبان سی شارپ و جاوا، یک نفر به زبان جاوا و پایتون، پنج نفر به زبان سی شارپ و پایتون و تنها یک برنامه نویس به هر سه زبان فوق مسلط است.
تعداد برنامه نویسان کامپیوتری که به هیچ یک از این سه زبان تسلط ندارند را مشخص کنید.
همانطور که در اولین مسئله تمرین اصل گنجاندن در بالا انجام شد، با تعریف اطلاعات داده شده شروع کنید:
اجازه دهید U مجموعه ای از تمام برنامه نویسان کامپیوتری را نشان دهد و اجازه دهید J، C و P به ترتیب نشان دهنده مجموعه برنامه نویسان مسلط به جاوا، سی شارپ و پایتون باشند. بدین ترتیب:
|U| = 100
|J| = 45
|C| = 30
|پ| = 20
|J ∩ C| = 6
|J ∩ P| = 1
|C ∩ P| = 5
|J ∩ C ∩ P| = 1
اکنون ممکن است از نمودار ون استفاده کنیم. این به سه دایره نیاز دارد زیرا سه مجموعه درگیر است. ابتدا با پر کردن تقاطع مرکزی هر سه دایره شروع کنید: J ∩ C ∩ P. سپس از تفریق برای تعیین کاردینالیته بخش های باقی مانده استفاده کنید.
اکنون اطلاعات کافی برای پاسخ به این سوال در اختیار داریم:
تعداد برنامه نویسان کامپیوتری که به هیچ یک از این سه زبان تسلط ندارند را مشخص کنید.
به عبارت دیگر، ما باید کاردینالیته متمم مجموعه J ∪ C ∪ P را تعیین کنیم. |J ∪ C ∪ P| را محاسبه کنید ابتدا قبل از تعیین مقدار مکمل:
|J ∪ C ∪ P|
= 39 + 5 + 20 + 4 + 15 + 1
= 84
حالا متمم را محاسبه کنید:
|(J ∪ C ∪ P)' | = |U| – |J ∪ C ∪ P|
= 100 - 84
= 16
16 برنامه نویس به هیچ یک از این سه زبان مهارت ندارند.
این مثال سوال اصل شمول-حذف را می توان به صورت جبری حل کرد.
350 کشاورز در یک منطقه بزرگ وجود دارد. 260 عدد چغندر مزرعه، 100 عدد تربچه مزرعه، 70 عدد تربچه مزرعه، 40 عدد چغندر و تربچه مزرعه، 40 عدد سیب زمینی و تربچه و 30 عدد چغندر و سیب زمینی مزرعه. اجازه دهید B، Y، و R مجموعه مزارعی را نشان دهند که به ترتیب چغندر، یام و تربچه پرورش می دهند.
تعداد کشاورزانی که چغندر، یام و تربچه پرورش می دهند را تعیین کنید.
حروف برای نشان دادن مجموعه ها قبلاً در خود سؤال ارائه شده است (برخلاف مثال بالا). بنابراین، ما میتوانیم فوراً به اصلی بودن توجه کنیم:
|U| = 350
|B| = 260
|Y| = 100
|R| = 70
|B ∩ R| = 40
|Y ∩ R| = 40
|B ∩ Y| = 30
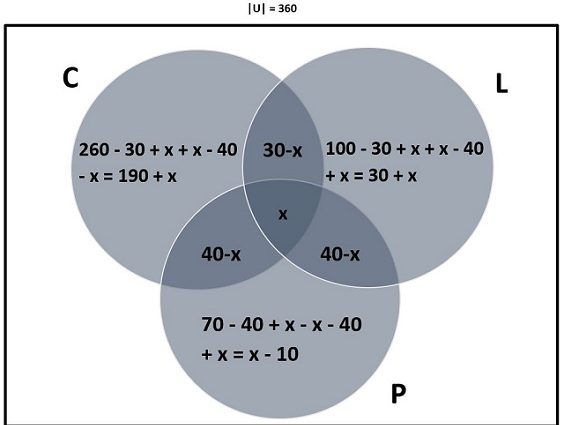
ما باید کاردینالیته تقاطع هر سه مجموعه را تعیین کنیم که |B ∩ Y ∩ R| است. این مجهولی است که می توانیم به صورت جبری تعیین کنیم. نمودار ون را با اطلاعات داده شده پر کنید. از x برای نشان دادن |B ∩ Y ∩ R| استفاده کنید .
اجازه دهید x کشاورزان چغندر، یام و تربچه پرورش دهند. یعنی اجازه دهید
|B ∩ Y ∩ R| = x
حالا x را به صورت جبری حل کنید:
|U|= 350 = 190 + x + (30 – x ) + x + (40 – x ) + (40 – x ) + 30 + x + x – 10
350 = 320 + x
x = 30
بنابراین 30 کشاورز چغندر، سیب زمینی و تربچه پرورش می دهند.
2018-11-21
بگذارید A مجموعه Painters
B باشد مجموعه Plumbers
C مجموعه برقکاران باشد.
داده شده،
|A| = 45
|B| = 50
|C| = 50
نامزد ماهر در هر سه حوزه
|A∩B∩C| = 15
همه آنها حداقل در یکی از این زمینه ها مهارت دارند. از این رو
|AUBUC| = 80
تعداد داوطلبانی که دقیقاً در 2 زمینه مهارت داشتند
= |A∩B| + |A∩C| + |B∩C|
با اصل گنجاندن – حذف،
|AUBUC| = |A| + |B| + |C|- [ |A∩B| + |A∩C| + |B∩C| ] + |A∩B∩C|
[ |A∩B| + |A∩C| + |B∩C| ] = |A| + |B| + |C| + |A∩B∩C| – |AUBUC|
= 45 + 50 + 50 + 15 - 80
= 80
لطفاً هر کسی این مشکل را حل کند،
در یک سایت ساخت و ساز، خورخه مسئول استخدام کارگران ماهر برای پروژه است. از 80 داوطلبی که با او مصاحبه کرد، متوجه شد که
45 نفر نقاش،
50 نفر برق،
50 نفر لوله کش،
15 نفر در هر سه زمینه مهارت داشتند و
همه آنها حداقل در یکی از این زمینه ها مهارت داشتند.
اگر همه کسانی را که دقیقاً در 2 زمینه مهارت داشتند را استخدام می کرد، چند نامزد استخدام می شد؟
بیت کوین در 24 ساعت تا ساعت 4:30 بعد از ظهر در هنگ کنگ با 0.11 درصد افزایش به 27933 دلار آمریکا رسید. اولین ارز دیجیتال جهان در طول هفته 0.62 درصد افزایش یافت.به سوالات زیر پاسخ دهید
ارزش بیت کوین در ابتدای روز چند دلار بوده است؟
ارزش بیت کوین در ابتدای هفته چند دلار بوده است؟
ارزش بازار جهانی ارزهای دیجیتال با 0.44 درصد کاهش به 1.18 تریلیون دلار در 24 ساعت تا ساعت 4:30 بعد از ظهر در هنگ کنگ رسید، در حالی که حجم کل معاملات بازار کریپتو با 11.56 درصد کاهش به 36.18 میلیارد دلار آمریکا رسید.
تبدیل تجانس یکی از چهار نوع تبدیل در هندسه است.
تجانس تغییر شکلی است که تصویری مشابه شکل اصلی، اما اندازه متفاوت ایجاد می کند. ایزومتری نیست ارقام مشابه را تشکیل می دهد.
به عبارت ساده، تجانس به این معنی است که فقط شکل داده شده را بدون چرخش یا هر چیز دیگری اندازه گیری می کند.
تجانس فاکتور مقیاس " k" :
(x، y) -----> ( k x، k y)
هنگامی که دانش آموزان قانون ذکر شده در بالا را که باید برای تبدیل تجانس اعمال کنند را درک کنند، می توانند به راحتی یک شکل را تغییر شکل دهند.
برای مثال، اگر بخواهیم تبدیل تجانس نقطه (5، 3) را برای ضریب مقیاس "k = 2" انجام دهیم، پس از تبدیل، نقطه (10، 6) خواهد بود.
در اینجا، قانونی که ما اعمال کرده ایم این است
(x، y) -------> (kx، ky)
برای k = 2، به دست می آوریم
(5، 3) -------> (10، 6)
برای درک بهتر، مثال زیر را در نظر می گیریم.
سوال:
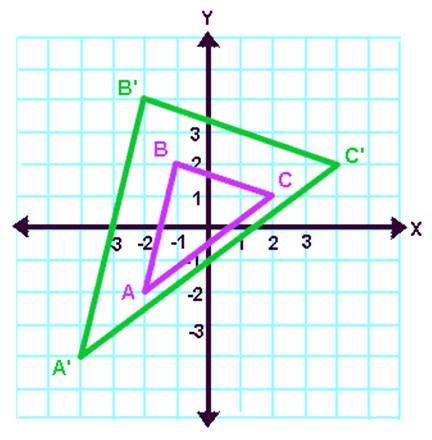
فرض کنید A(-2، -2)، B(-1، 2) و C(2، 1) سه رأس یک مثلث باشند. اگر این مثلث برای ضریب مقیاس "k = 2" گشاد شود، رئوس جدید A'، B' و C' چه خواهند بود؟
راه حل:
مرحله 1:
ابتدا باید قانون صحیحی را که باید در این مشکل اعمال کنیم، بدانیم.
گام 2 :
در اینجا، مثلث برای ضریب مقیاس "k = 2" گشاد شده است.
بنابراین، قانونی که باید در اینجا اعمال کنیم این است
(x, y) -------> (kx , ky)
مرحله 3:
بر اساس قانون داده شده در مرحله 1، باید رئوس مثلث گشاد شده A'B'C' را پیدا کنیم.
مرحله 4:
(x، y) -----> (kx، ky)
A(-2، -2) -------> A'(-4، -4)
B(-1، 2) -------> B'(-2، 4)
C(2، 1) -------> C'(4، 2)
مرحله 5:
رئوس مثلث متسع هستند
A'(-4، -4)، B(-2، 4) و C'(4، 2)
1. ابتدا باید رئوس تصویر پیش را رسم کنیم.
2. در مسئله فوق رئوس تصویر پیشین هستند
A(-2، -2)، B(-1، 2) و C(2، 1)
3. وقتی این نقاط را روی یک کاغذ گراف رسم می کنیم، شکل پیش تصویر (شکل اصلی) به دست می آید.
4. وقتی شکل داده شده را برای "k = 2" گشاد می کنیم، باید فرمول را اعمال کنیم
(x، y) -------> (kx، ky)
5. زمانی که فرمول را اعمال می کنیم، رئوس تصویر زیر را بدست می آوریم (شکل گشاد شده).
6. در مسئله فوق رئوس تصویر هستند
A'(-4، -4)، B'(-2، 4) و C'(4، 2)
7. وقتی این نقاط را روی کاغذ گراف رسم می کنیم، شکل تصویر (شکل گشاد شده) را به دست می آوریم.
مثلث قائم الزاویه نشان داده شده است. مساحت این شکل را مشخص کنید.
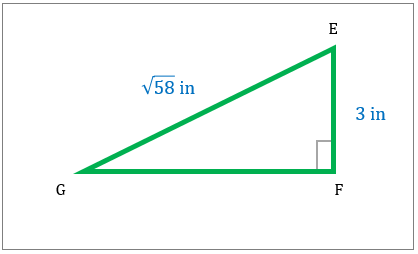 |
مساحت مثلث قائم الزاویه را در تصویر زیر بیابید.
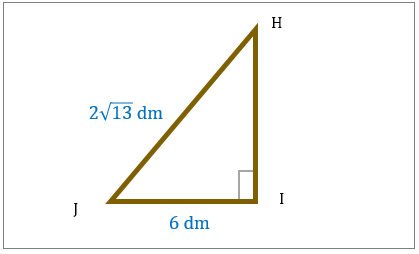 |
با کمک قضیه فیثاغورث، که با مساحت مثلث مطابقت دارد؟
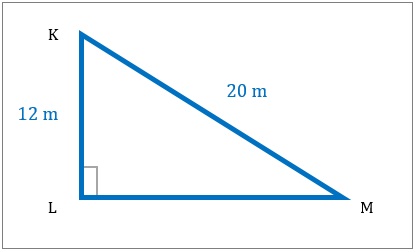 |
مثلث قائم الزاویه را تحلیل کنید و مساحت آن را محاسبه کنید.
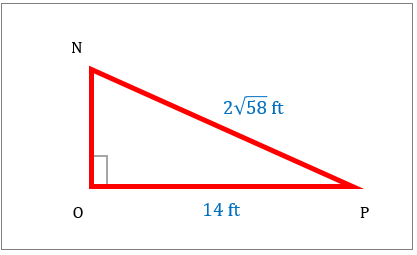 |
پاسخ به انتخاب ها
مساحت مثلث قائم الزاویه ساخته شده را در نمودار با استفاده از قضیه فیثاغورث تعیین کنید.
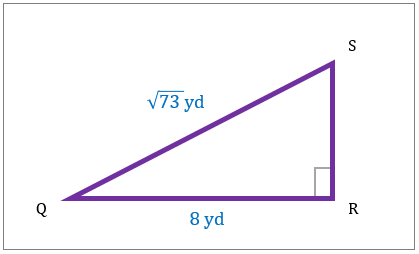 |
مثلث قائم الزاویه را در نظر بگیرید و مساحت آن را حل کنید.
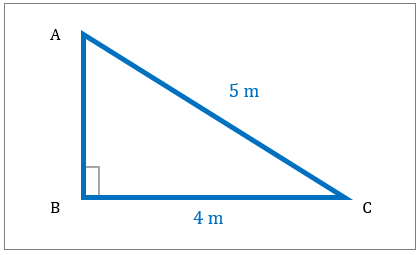 |
مساحت مثلث قائم الزاویه را که در زیر نشان داده شده است محاسبه کنید.
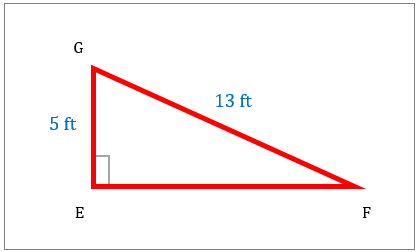 |
مثلث قائم الزاویه در زیر نشان داده شده است. مساحت این شکل را مشخص کنید.
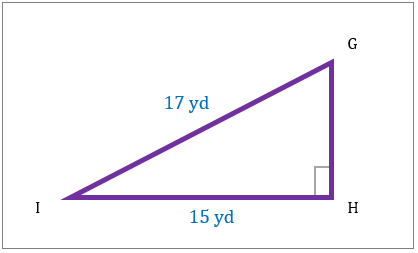 |
مساحت مثلث قائم الزاویه را در تصویر زیر بیابید.
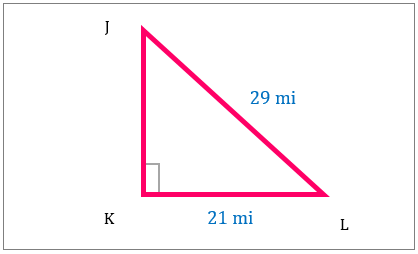 |
با کمک قضیه فیثاغورث، مساحت مثلث کدام است؟
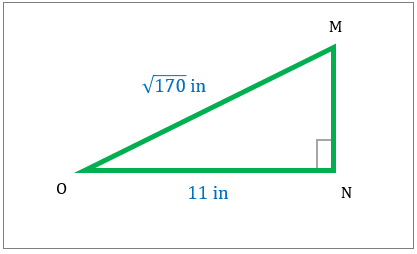 |
مثلث قائم الزاویه را تحلیل کنید و مساحت آن را محاسبه کنید.
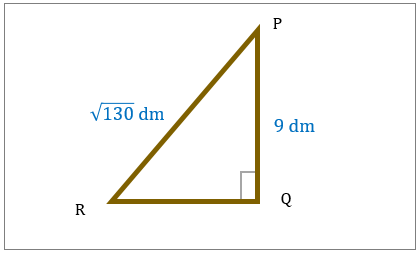 |
مساحت مثلث قائم الزاویه ساخته شده را در نمودار با استفاده از قضیه فیثاغورث تعیین کنید.
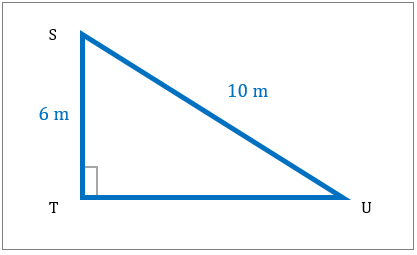 |
به مثلث در زیر مراجعه کنید. مساحت شکل نشان داده شده چقدر است؟
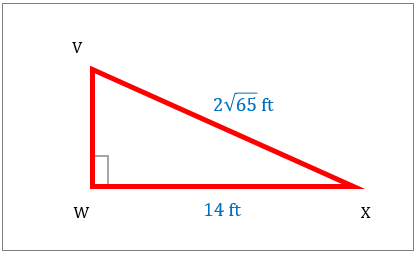 |
مثلث قائم الزاویه را در نظر بگیرید و مساحت آن را حل کنید.
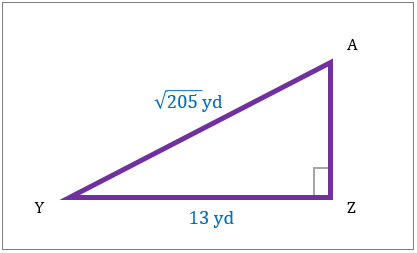 |
مساحت مثلث قائم الزاویه را که در زیر نشان داده شده است، محاسبه کنید.
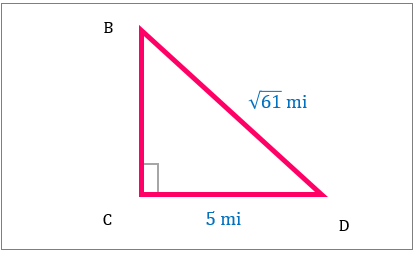 |
مساحت مثلث قائم الزاویه ساخته شده را در نمودار با استفاده از قضیه فیثاغورث تعیین کنید.
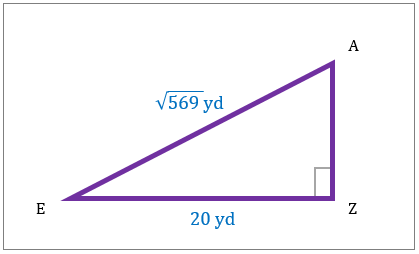 |
مثلث قائم الزاویه تحلیل کنید و مساحت آن را محاسبه کنید.
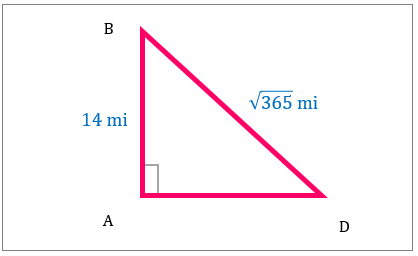 |
با کمک قضیه فیثاغورث، مساحت مثلث کدام است؟
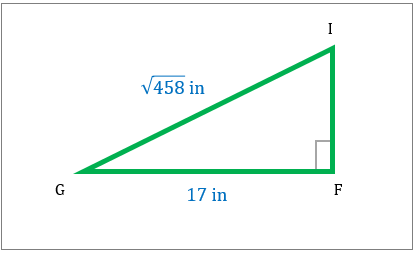 |
مساحت مثلث قائم الزاویه را در تصویر زیر بیابید.
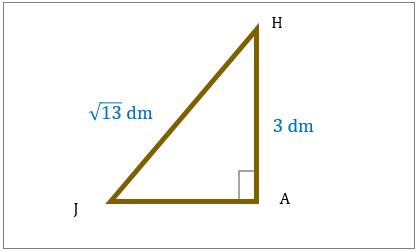 |
مثلث قائم الزاویه در زیر نشان داده شده است. مساحت این شکل را مشخص کنید.
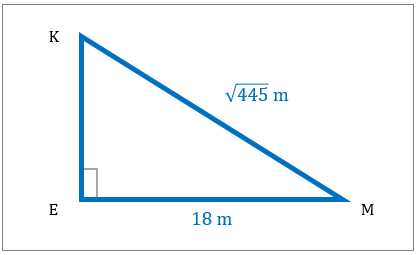 |
مساحت مثلث قائم الزاویه را که در زیر نشان داده شده است، محاسبه کنید.
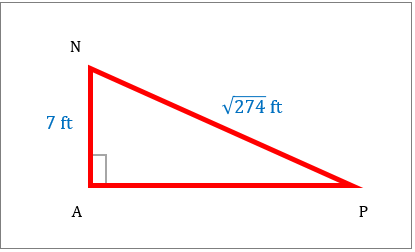 |
مثلث قائم الزاویه را برای مساحت آن در نظر بگیرید.
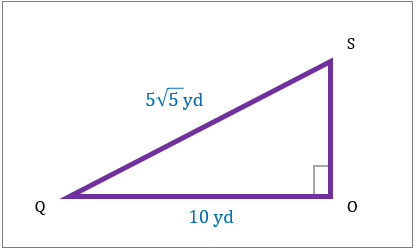 |
مثلث قائم الزاویه در زیر نشان داده شده است. مساحت این شکل را مشخص کنید.
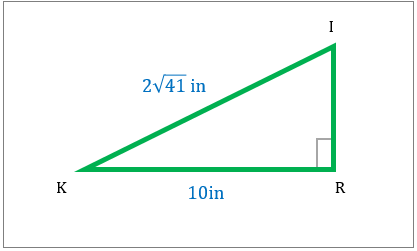 |
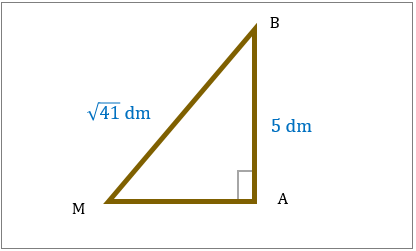 |
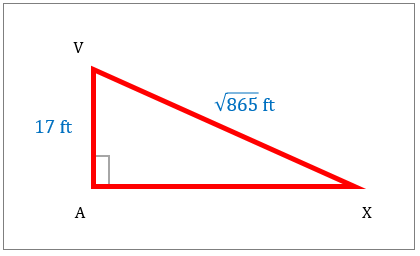
مثلث قائم الزاویه در زیر نشان داده شده است. مساحت این شکل را مشخص کنید.
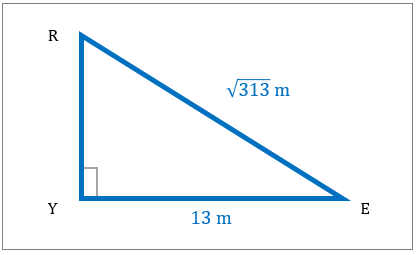 |
 |
 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.