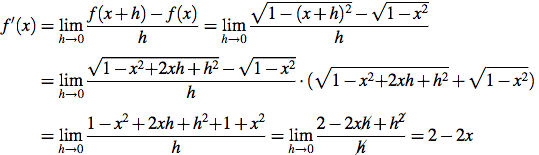تمرین 2

نقطه را در تابع| y = | x ² - 5x + 6 پیدا کنید جایی که هیچ مشتقی ندارد نتیجه را با نمایش گرافیکی توجیه کنید.

تمرین 3

پیوستگی و مشتق پذیری بودن عملکرد تعریف شده توسط:

تمرین 4

با توجه به تابع:

برای چه مقادیری ازa یک تابع مشتق پذیریاست؟

تمرین 5

مقادیر a و b را در جایی که عملکرد زیر پیوسته و مشتق پذیریاست تعیین کنید:

تمرین 6

مقادیر a و b را که عملکرد برای همه نقاط مشتق پذیر است تعیین کنید:

تمرین 7

امتیازهایی را پیدا کنید که |y = 250 - | x² −1  هیچ مشتقی ندارد

تمرین 8

مشخص کنید که مقادیر a و b کدام تابع به طور پیوسته و مشتق پذیراست:

راه حل تمرین 1

نقطه را در عملکرد y = | x + 2 | پیدا کنید جایی که هیچ مشتقی ندارد نتیجه را با نمایش گرافیکی توجیه کنید.

عملکرد پیوسته است.

f '(- 2) - = f1 f' (- 2) + = 1

این ماده در P (2 −) هیچ مشتقی ندارد.

راه حل تمرین 2

نقطه را در تابع|y = | x ² - 5x + 6 پیدا کنید جایی که هیچ مشتقی ندارد نتیجه را با نمایش گرافیکی توجیه کنید.

عملکرد مداوم است.

f '(2) - = f1 f' (2) + = 1

f '(3) - = f1 f' (3) + = 1

این تابع در: x = 2 و x = 3 یا در نقاط P 1 (2،0) و P 2 (3،0) مشتق پذیر نیست.

راه حل تمرین 3

پیوسته و متفاوت بودن عملکرد تعریف شده توسط:

این عملکرد در x = 0 مداوم نیست زیرا هیچ تصویری ندارد. بنابراین قابل تشخیص نیست.

عملکرد مداوم است.

عملکرد در هر نقطه‌ای قابل تفکیک نیست.

راه حل تمرین 4

با توجه به عملکرد:

برای چه مقادیری از یک تابعمشتق پذیر است؟

متفاوت در a = 1

برای x = −1 ، پیوسته نیست.

راه حل تمرین 5

مقادیر a و b را در جایی که عملکرد زیر پیوسته و متفاوت است تعیین کنید:

راه حل تمرین 6

مقادیر a و b را که عملکرد برای همه نقاط مشتق پذیراست تعیین کنید:

یک عملکرد متفاوت باید پیوسته باشد. در این حالت تابع برای x = 0 پیوسته نیست ، یعنی هیچ مقداری برای a و b وجود ندارد که عملکرد را پیوسته کند.

بنابراین ، هیچ مقداری از a و b وجود ندارد که عملکرد برای آنها مشتق پذیرباشد.

راه حل تمرین 7

امتیازهایی را پیدا کنید که y = 250 - | x² −1 | هیچ مشتقی ندارد

عملکرد پیوسته است.

در x = −1 و x = 1 مشتق پذیر نیست.

راه حل تمرین 8

مشخص کنید که مقادیر a و b کدام تابع به طور پیوسته و متفاوت است:

برای a = - 1 و b = 4 ، عملکرد پیوسته است.

در x = 0 مشتق پذیر نیست.

در x = 2 مشتق پذیراست.

توابع معکوس

مشتقات عملکردهای مختلف دیگر را می توان با قاعده زنجیره ای و ترکیب توابع معکوس بدست آورد. روش به شرح زیر است:

فرض کنید f ( x ) متفاوت است و عملکرد معکوس آن (f -1 ( x  نیز متفاوت است. هنگامی که آنها تشکیل شده اند ، نتیجه این است

f -1 ( f ( x )) = x . 

برای یافتن مشتقات( f ( x  ، مشتق توابع تشکیل شده ، که از طریق قانون زنجیره بدست آمده است ، نتیجه زیر را می دهد:

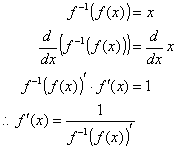
فرض کنید f ( x ) = ln x . سپس f -1 ( x ) = e x . سپس f -1 ( f ( x )) '= e ln x = x . بنابراین ، موارد زیر:

سایر مشتقات بدست آمده با این روش عبارتند از:

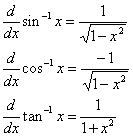
توابع هیپر بولیک

کارکردهای چربی مانند تعریف شده اند

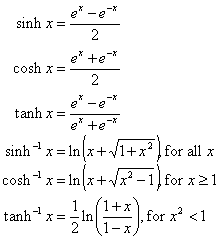
مشتقات آنها با قوانینی که در بالا ذکر شد قابل دستیابی است:

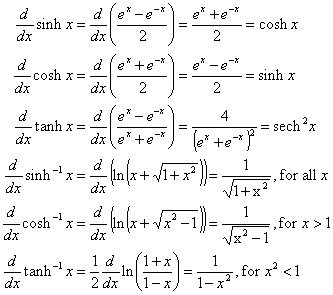
توابع پارامتری

معادلات پارامتری حرکت نقطه P را به عنوان توابع مستقل پارامتر t توصیف می کند زیرا در مورد صفحه xy سرگردان است . X - و Y- مختصات هستند

x f ( t ) و y = g ( t ) 

منحنی های پارامتری در تنوع ذهن آزاردهنده قرار می گیرند. هر انتخاب از دو معادله و t -interval یک منحنی پارامتری تولید می کند. اغلب نتیجه زیبا ، مفید ، جالب یا هر سه است.

میزان تغییر موقعیت ، P = ( f ( t ) ، g ( t ))   در امتداد یک منحنی پارامتری تعریف شده توسط

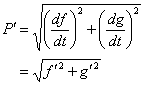
این اغلب به عنوان سرعت ذره تصور می شود زیرا برای بسیاری از کاربردها متغیر مستقل t زمان را نشان می دهد. شیب منحنی پارامتری توسط داده شده است

معادلات قطبی

موقعیت یک نقطه در صفحه xy را می توان به صورت قطبی بیان کرد ، یعنی از نظر فاصله آن (شعاع ، r ) از مبدا و زاویه ، q ، بردار شعاع آن با x -axis مثبت ایجاد می کند . نمودارهای دکارتی (مستطیلی) غالباً y = f ( x ) نشان داده می شوند. چنین توابع همچنین می توانند به صورت قطبی r = f ( q ) نشان داده شوند. تبدیل نقاط یا معادلات بین سیستمها از طریق معادلات تبدیل است:

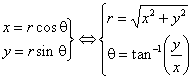
مشتقات x و y با توجه به q توسط قانون محصول قابل دستیابی است :

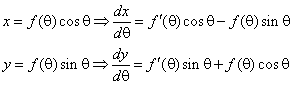
بنابراین شیب منحنی قطبی داده می شود

بردارها

بردارها مقادیری هستند که هم از نظر اندازه و هم جهت دارند. برای یک بردار از فرم

 بزرگی آن است

و جهت آن با توجه به مثبت x است

به این ترتیب ، بردارها واقعاً توابع پارامتری هستند. بنابراین ، نرخ تغییر یک بردار تعیین کننده نرخ تغییر برای اجزای آن است:

قانون Quotient:

هنگامی که یک تابع از دو عملکرد است یا می توان آنرا به عنوان چنین ذاتی تجزیه کرد ، آنگاه قضیه زیر به ما اجازه می دهد تا مشتق آن را بیابیم:

اگر y = f ( x ) / g ( x ) ،

راه دیگر برای نوشتن این مقاله ، با استفاده از نماد Leibniz است

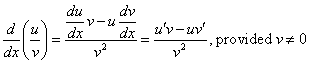
توجه كنيد كه مشتق يك كاركرد فقط توابع مشتقات آنها نيست. این مشتق تا حدودی پیچیده تر است. به این معنا که،

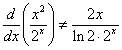
در عوض ، ما داریم

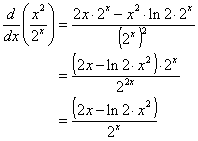
مثال ها:

1. یک عملکرد منطقی از چند جمله ای:

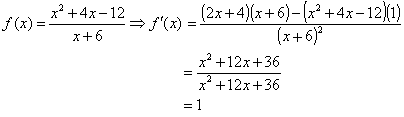
شما باید تأیید کنید که این نتیجه ای است که ما می توانیم به دست بیاوریم که ابتدا عملکرد منطقی را ساده کرده بودیم ، سپس مشتق را می گرفتیم.

2. عملکرد منطقی دیگری که نمی توان جبری را ساده کرد:

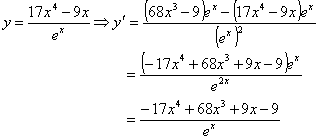
3. نمونه ای از توابع عددی تعریف شده. بگذارید f (2) = 1، f '(2) = -1 ، g (2) = -3 و g' (2) = 4. مشتقات( f ( x ) / g ( x  را در x = 2 پیدا کنید. 

راه حل: براساس قانون quent ، مشتق محصول f و g در x = 2 است

هنگامی که یک تابع ضرب دو تابع است یا می تواند به عنوان چنین کالایی تجزیه شود ، آنگاه قضیه زیر به ما اجازه می دهد تا مشتق آن را بیابیم:

اگر( y = f ( x ) g ( x  ، سپس

[ f ( x ) g ( x )] '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

راه دیگر برای نوشتن این مقاله ، با استفاده از نماد Leibniz است

توجه کنید که مشتق یک محصول از توابع فقط محصول مشتقات آنها نیست؛ این مشتق تا حدودی پیچیده تر است. به این معنا که،

در عوض ، ما داریم

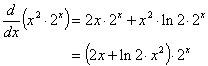
مثال ها:

1. صرب 

f ( x ) = (2 x + 1) ( x 2 - 2).

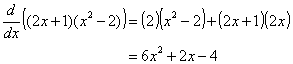
باید توجه کنید که اگر ابتدا محصول را ساده کردید ، سپس مشتق آن را بگیرید ، نتیجه همان  خواهد بود.

2. مثال دیگر:

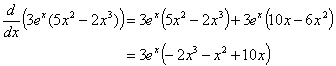
فاکتورسازی نتیجه در انتها معمولاً برای جبری یافتن نقاط بحرانی و فواصل افزایش / کاهش مناسب است.

3. نمونه ای از توابع عددی تعریف شده. بگذارید f (2) = 1، f '(2) = -1 ، g (2) = -3 و g' (2) = 4. مشتقات (f ( x ) g ( x  را در x = 2 پیدا کنید .

راه حل: طبق قانون ضرب ، مشتق ضرب f و g در x = 2 است

f '(2) g (2) + f (2) g ' (2) = (-1) (- 3) + (1) (4) = 7

مشتقات توابع نمایی.  

از تعریف مشتق می توان نتیجه گرفت

مثال ها:

1. مشتق 2 x .

2. مشتق 5 (4.6) x .

3. مشتق (ln3) x .

4- مشتق e x .

این نتیجه نهایی نتیجه این واقعیت است که ln e = 1.

قانون توان برای مشتقات می توان با استفاده از تعریف مشتق و قضیه دو جمله ای به دست آمد. نتیجه این قضیه زیر است:

اگر f ( x ) = x n  آنگاه f '( x ) = nx n- 1

چند جمله ای ها مجموع توابع توان هستند. برای به دست آوردن مشتقات آنها ، باید حقایق زیر را تعیین کنیم: 

جایی که c مستقل از x است ، و 

در حالی که ابتدا این قوانین برای توابع توان و چند جمله ای ها اعمال می شوند ، آنها برای هر کارکردی کار می کنند.

مثال ها:

1. چند جمله ای با عوامل مثبت و منفی.

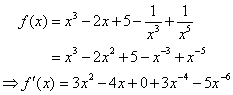
    در این مثال ، ما عبارات منطقی را به عنوان اصطلاحات قدرت با منافع منفی بازنویسی می کنیم.

2. یک عملکرد منطقی با یک اصطلاح واحد در مخرج.

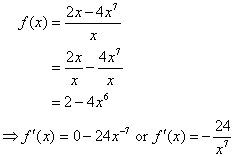
در این مثال ، ما کسری را تقسیم می کنیم و قبل از گرفتن مشتق ساده می کنیم. این اغلب ساده تر از به کار بردن قانون امتیاز است.

بازگشت به بالا.

3. تابعی با اصطلاح رادیکال.

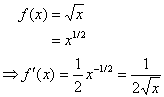
در این مثال ، ما رادیکال را از نظر یک عامل منطقی بازنویسی می کنیم. نتیجه نهایی چیزی است که ما با استفاده از تعریف مشتق ، مشتق را پیدا می کنیم.

4- کارکرد دیگری با اصطلاحات پیچیده تر.

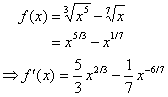
مثال 1: مشتق تابع f داده شده را پیدا کنید

راه حل برای مثال 1: تابع f ضرب دو تابع است: U = x 2 - 5 و V = x 3 - 2 x + 3؛ از این رو

ما از قانون ضرب  برای تمایز f به شرح زیر استفاده می کنیم:

که در آن U و V به ترتیب مشتقات U و V هستند و توسط آنها داده می شود

جایگزین برای به دست آوردن

گسترش ، گروه بندی و ساده سازی کنید

مثال 2: اولین مشتق تابع f داده شده توسط آن را محاسبه کنید 

راه حل برای مثال 2: این تابع ممکن است ضرب تابع  U = √x + 2x و V = 4x 2 - 1 محسوب شود ، از این رو استفاده از قانون ضرب

برای افزودن موارد فوق ، باید همه اصطلاحات را به عنوان کسری با مخرج مشترک بنویسید. 

بسط دادن 

و گروه برای به دست آوردن نتیجه نهایی برای مشتق f به شرح زیر است. 

مثال 3: اولین مشتق تابع f داده شده توسط آن را محاسبه کنید 

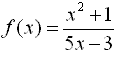
 راه حل به مثال 3: 
تابع داده شده به عنوان نسبت دو تابع در نظر گرفته می شود: U = x 2 + 1 و V = 5x - 3 و با استفاده ازقاعده ی تقسیم برای تمایز f از این روش استفاده می شود. 

گسترش و گروه را بدست آورید تا( f '(x را به شرح زیر بدست آورید 

مثال 4: اولین مشتق تابع f داده شده توسط آن را محاسبه کنید 

راه حل برای مثال 4: تابع f ، از دو تابع استفاده می کند ، از این رو استفاده از قانون تقسیم است
 

همه عبارات را در اعداد بنویسید به طوری که آنها دارای مخرج یکسان  باشند 

برای به دست آوردن f '(x) عبارات را مانند گروه گسترش داده و گروه بندی کنید 

مثال 5: اولین مشتق تابع f داده شده توسط آن را محاسبه کنید 

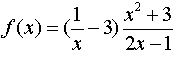
راه حل برای مثال 5: تابع f داده شده در بالا ممکن است ضرب توابع (U =( 1 / x - 3 و (V = (x 2 + 3) / (2x - 1در نظر گرفته شود و تابع V ممکن است به عنوان سود دهنده در نظر گرفته شود. دو تابع x 2 + 3 و 2x - 1. ما از قاعده ضرب برای f و قاعده مقدار برای V به شرح زیر استفاده می کنیم

همه اصطلاحات را بر روی مخرج مشترک تنظیم کنید 

برای به دست آوردن مشتق f 'گسترش و گروه دهید. 

مثال 6: اولین مشتق تابع f داده شده توسط آن را محاسبه کنید 

راه حل برای مثال 6: روش های مختلفی برای یافتن مشتقات عملکرد f در بالا وجود دارد. یکی از آنها در نظر گرفتن تابع f به عنوان ضرب تابع U = sqrt x و

(V = (2x - 1) (x 3 - x است و همچنین V را به عنوان ضرب (2x - 1) و (x^ 3 - x ) در نظر می گیریم .  و قانون ضرب را به شرح زیر در f و V اعمال کنید

یک مخرج مشترک را برای همه شرایط تنظیم کنید 

برای بدست آوردن مشتق f ، عبارات گسترده و گروهی را گروه بندی کنید. 

مثال 7: مشتق تابع f داده شده را پیدا کنید 

راه حل به عنوان مثال 7: عملکرد داده شده از فرم U 4 است که U = x 3 + 4. استفاده از قانون تمایز زنجیره ای f را به شرح زیر می دهد.
 

U را محاسبه کرده و در زیر جایگزین کنید تا f را بدست آورید 

مثال 8: مشتق تابع f داده شده را پیدا کنید 

راه حل برای مثال 8: عملکرد f از فرم U 3 است که در آن( U = (x - 1) / (x + 3 است. برای بدست آوردن f از جدول زیر ، زنجیره اعمال کنید
 

U را محاسبه کرده و با استفاده از قاعده بزرگ ، و جایگزین آن را بگیرید 

عبارات مشابه و گروهی را گسترش دهید تا فرم نهایی برای مشتقات f را بسازید. 

مثال 9: مشتق تابع f داده شده را پیدا کنید 

راه حل برای مثال 9: تابع داده شده از فرم sqrt U با U = x 3 + 2 x + 1 است. 'U را محاسبه کرده و از قاعده زنجیره ای برای بدست آوردن استفاده کنید.
 

مثال 10: مشتق تابع f داده شده را پیدا کنید 

راه حل برای مثال 10: عملکرد داده شده از فرم U 3/2 با U = x 2 + 5 است. قانون زنجیره را به شرح زیر اعمال کنید
 

برای بدست آوردن  مشتق  ، U را محاسبه ، جایگزین و ساده کنید. 

مماس ، وتر و سکوت یک دایره

این تصور بصری که یک خط مماس "منحنی" را لمس می کند ، می تواند با در نظر گرفتن توالی خطوط مستقیم ( خطوط جداکننده ) که از دو نقطه A و B عبور می کند ، صریح تر شود ، آنهایی که بر روی منحنی تابع قرار دارند. مماس در A محدودیتی است که نقطه B تقریباً به A نزدیک یا تمایل پیدا می کند .وجود و منحصر به فرد بودن خط مماس ، بستگی به نوع خاصی از روان بودن ریاضی دارد ، که به آن "متفاوت بودن" معروف است. به عنوان مثال ، اگر دو قوس دایره ای در یک نقطه تیز (یک راس) قرار بگیرند ، هیچ مماس مشخص شده منحصر به فرد در راس وجود ندارد ، زیرا حد پیشرفت خطوط ترشح بستگی به جهتی دارد که در آن "نقطه B"به راس نزدیک می شود.

در بیشتر نقاط ، مماس بدون عبور از آن منحنی را لمس می کند (گرچه ممکن است در صورت ادامه ، از منحنی در سایر نقاط دور از نقطه مماس عبور کند). نقطه ای که مماس (در این مرحله) از منحنی عبور می کند ، نقطه عطف نامیده می شود . دایره ها ، پارابولا ها ، هایپربولاها و بیضی ها هیچ نقطه احتقایی ندارند ، اما منحنی های پیچیده تری مانند نمودار یک تابع مکعب ، که دقیقاً یک نقطه تورم دارد یا سینوسی وجود دارد که در هر دوره از آن دارای دو نقطه تورم است . سینوسی .

در مقابل ، ممکن است اتفاق بیفتد که منحنی کاملاً در یک طرف یک خط مستقیم قرار داشته باشد و از یک نقطه روی آن عبور کند ، اما هنوز این خط مستقیم یک خط مماس نیست. به عنوان مثال ، برای خطی كه از راس مثلث عبور كرده و در غیر این صورت تقاطع نداشته باشد - در صورتی كه خط مماس به دلایلی كه در بالا توضیح داده شد وجود ندارد. در هندسه محدب ، چنین خطوطی خطوط حمایت کننده خوانده می شوند .

در هر نقطه ، خط متحرک همیشه مطابق با منحنی است . شیب آن مشتق است . سبز مشتق مثبت ، علائم قرمز مشتق منفی و سیاه مشتق صفر را نشان می دهد. نقطه (x، y) = (0،1) که در آن مماس از منحنی عبور می کند ، حداکثر یا دقیقه نیست ، بلکه نقطه عطف است .

رویکرد تحلیلی [ ویرایش ]

ایده هندسی خط مماس به عنوان حد خطوط جداکننده به عنوان انگیزه ای برای روش های تحلیلی است که برای پیدا کردن صریح خطوط مماس استفاده می شود. سوال یافتن خط مماس به یک نمودار یا مشکل خط مماسیکی از سؤالات محوری بود که منجر به توسعه حساب در قرن 17 شد. در کتاب دوم هندسه خود ، رنه دکارت [8] درباره مشکل ساخت مماس به یک منحنی گفت: "و به جرات می گویم که این تنها مفیدترین و عمومی ترین مشکل در هندسه نیست که من می دانم ، بلکه حتی که من همیشه آرزو کرده ام بدانم ". [9]

توصیف بصری [ ویرایش ]

فرض کنید که یک منحنی به عنوان نمودار یک تابع ، y = f ( x ) داده شده است. برای یافتن خط مماس در نقطه p = ( a ، f ( a )) ، نقطه مجاور دیگری را در نزدیکی q = ( a + h ، f ( a + h )) در نظر بگیرید. شیب از خط قاطع عبور از ص و س به برابر استخارج قسمت تفاوت

با نزدیک شدن نقطه q به p ، که مربوط به کوچکتر و کوچکتر شدن h است ، مقدار اختلاف تفاوت باید به یک مقدار محدودکننده خاص k ، یعنی شیب خط مماس در نقطه p نزدیک شود . اگر k شناخته شده باشد ، معادله خط مماس را می توان در فرم شیب نقطه یافت:

توضیحات دقیق تر [ ویرایش ]

برای استدلال قبلی سختگیرانه ، باید توضیح داد که منظور از تفاوت سهم نزدیک به یک مقدار محدود کننده خاص k است . فرمول دقیق ریاضی توسط کوشی در قرن نوزدهم ارائه شده است و مبتنی بر مفهوم حد است . فرض کنید که نمودار یک استراحت و یا یک لبه تیز در ندارد ص و آن را نه بطور عمودی و نه خیلی نزدیک است نمودار ص . سپس مقدار منحصر به فردی از k به وجود می آید که با نزدیک شدن به h 0 ، اختلاف اختلاف به k نزدیک تر می شود و فاصله بین آنها در مقایسه با اندازه h ناچیز می شود ، در صورت hبه اندازه کافی کوچک است این منجر به تعریف شیب خط مماس به نمودار به عنوان حد اختلاف مقدار برای تابع f می شود . این حد مشتق تابع f در x = a است ، با علامت f  ′ ( a ). با استفاده از مشتقات می توان معادله خط مماس را به شرح زیر بیان کرد:

حساب محاسبه قوانینی را برای محاسبه مشتقات توابع که توسط فرمول ها ارائه می شود ، مانند عملکرد قدرت ، توابع مثلثاتی ، عملکرد نمایی ، لگاریتم و ترکیبات مختلف آنها فراهم می کند. بنابراین ، معادلات مماسها به نمودارهای همه این توابع ، و همچنین بسیاری دیگر ، با روشهای حساب می توان یافت.

ابزارک تصویر