دل نوشته ها ی نقش و آموزش ریاضی  

توابع معکوس

مشتقات عملکردهای مختلف دیگر را می توان با قاعده زنجیره ای و ترکیب توابع معکوس بدست آورد. روش به شرح زیر است:

فرض کنید f ( x ) متفاوت است و عملکرد معکوس آن (f -1 ( x  نیز متفاوت است. هنگامی که آنها تشکیل شده اند ، نتیجه این است

f -1 ( f ( x )) = x . 

برای یافتن مشتقات( f ( x  ، مشتق توابع تشکیل شده ، که از طریق قانون زنجیره بدست آمده است ، نتیجه زیر را می دهد:

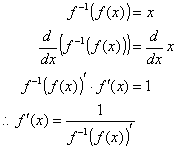
فرض کنید f ( x ) = ln x . سپس f -1 ( x ) = e x . سپس f -1 ( f ( x )) '= e ln x = x . بنابراین ، موارد زیر:

سایر مشتقات بدست آمده با این روش عبارتند از:

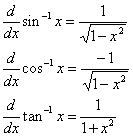
توابع هیپر بولیک

کارکردهای چربی مانند تعریف شده اند

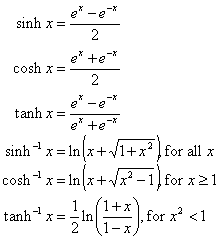
مشتقات آنها با قوانینی که در بالا ذکر شد قابل دستیابی است:

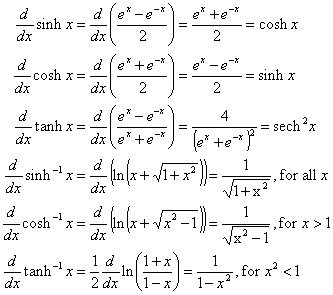
توابع پارامتری

معادلات پارامتری حرکت نقطه P را به عنوان توابع مستقل پارامتر t توصیف می کند زیرا در مورد صفحه xy سرگردان است . X - و Y- مختصات هستند

x f ( t ) و y = g ( t ) 

منحنی های پارامتری در تنوع ذهن آزاردهنده قرار می گیرند. هر انتخاب از دو معادله و t -interval یک منحنی پارامتری تولید می کند. اغلب نتیجه زیبا ، مفید ، جالب یا هر سه است.

میزان تغییر موقعیت ، P = ( f ( t ) ، g ( t ))   در امتداد یک منحنی پارامتری تعریف شده توسط

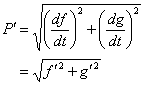
این اغلب به عنوان سرعت ذره تصور می شود زیرا برای بسیاری از کاربردها متغیر مستقل t زمان را نشان می دهد. شیب منحنی پارامتری توسط داده شده است

معادلات قطبی

موقعیت یک نقطه در صفحه xy را می توان به صورت قطبی بیان کرد ، یعنی از نظر فاصله آن (شعاع ، r ) از مبدا و زاویه ، q ، بردار شعاع آن با x -axis مثبت ایجاد می کند . نمودارهای دکارتی (مستطیلی) غالباً y = f ( x ) نشان داده می شوند. چنین توابع همچنین می توانند به صورت قطبی r = f ( q ) نشان داده شوند. تبدیل نقاط یا معادلات بین سیستمها از طریق معادلات تبدیل است:

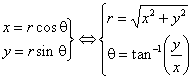
مشتقات x و y با توجه به q توسط قانون محصول قابل دستیابی است :

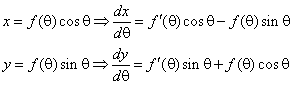
بنابراین شیب منحنی قطبی داده می شود

بردارها

بردارها مقادیری هستند که هم از نظر اندازه و هم جهت دارند. برای یک بردار از فرم

 بزرگی آن است

و جهت آن با توجه به مثبت x است

به این ترتیب ، بردارها واقعاً توابع پارامتری هستند. بنابراین ، نرخ تغییر یک بردار تعیین کننده نرخ تغییر برای اجزای آن است: