x+1/x=2 و x(1/x)=1 ===> S=2 ,P=1===>
x=1 ===>
x^100 +1/x^100=1+1=2
x+1/x=2 و x(1/x)=1 ===> S=2 ,P=1===>
x=1 ===>
x^100 +1/x^100=1+1=2
از قاعده تقسیم استفاده می کنیم
با توجه به y = (ax ^2 + cotx) (p + q cosx)
از قاعده ضرب استفاده می کنیم
به کارگیری مفهوم قانون زنجیره ای:
بهترین جواب این سوال شامل مفهوم قانون زنجیره و قانون ضرب می شود. با توجه به y = (2x – 7)^ 2 (3x + 5) ^3 استفاده از قانون مشتق ضرب
(A) -15/(3x+5)^2
(B) -15/(4x+5)^2
(C)-5/(4x+5)^2
(D) -13/(4x+5)^2
ایده اصلی
مثال. از قضیه فشار برای نشان دادن اینکه lim x→1 x^ √2 = 1 استفاده کنید.
خواندن ایده ها: حتی خود قضیه نیز واضح نیست.
توضیح تصویری:
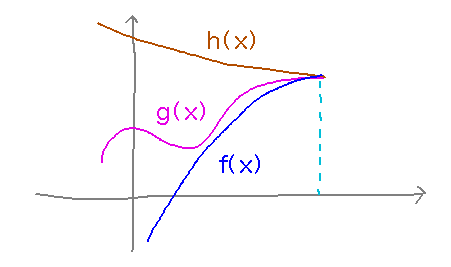
بردن. اگر تابع g بین توابع f و h قرار داشته باشد و f و h در نقطهای یک حد داشته باشند، از آنجایی که g بین آنها قرار دارد، باید در آن نقطه نیز آن حد را داشته باشد.
در اینجا نحوه استفاده از این ایده برای نشان دادن اینکه lim x→1 x √2 = 1 آورده شده است:
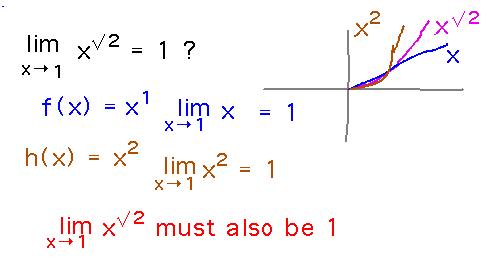
مشتقات مرتبه بالاتر با گرفتن مکرر مشتقات مشتقات حاصل به دست می آیند. بنابراین، مشتق دوم یک تابع، مشتق مشتق اول آن است و مشتق مرتبه n ممکن است با گرفتن مشتق از مشتق مرتبه st (n - 1) به دست آید. ممکن است از نمادهای مختلفی برای نشان دادن مشتقات متوالی استفاده شود: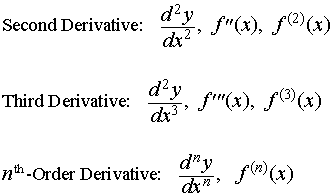
مثال شماره 1 :
پنج مشتق اول sin x را بیابید .
راه حل شماره 1 :
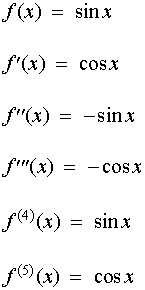
مثال شماره 2 :
سه مشتق اول
4 x ^3 + 2 x + 6
را بیابید.
راه حل شماره 2 :
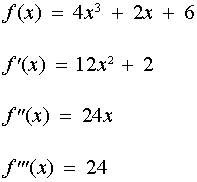
برای تابع متمایز f با یک تابع معکوس y = f ^− 1 ( x )، چنین است که:
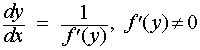
مثال :
مشتق معکوس f ( x ) = x^ 3 + 1 را تعیین کنید
راه حل :
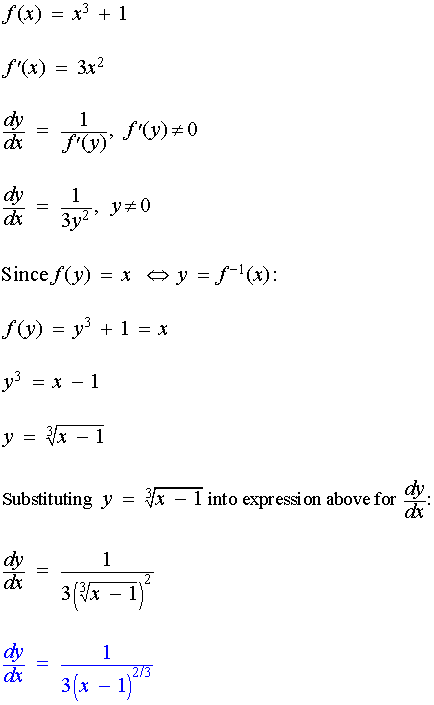
برای p ( x ) = m [ n ( x )] = m o n :
p '( x ) = m '[ n ( x )] n ' ( x )
مثال شماره 1 :
مشتق ( x − 1/2 ) 3 را با استفاده از قانون زنجیره ای پیدا کنید.
راه حل شماره 1 :
با استفاده از قانون زنجیره ای با n ( x ) = x − 1/2 و m ( x ) = x 3 نتیجه می شود که
n '( x ) = ( − ½ ) x − 3/2
و
m '[ n ( x )] = 3( x − 1/2 ) 2 = 3 x − 1
p '( x ) = m ' [ n ( x )] n ' ( x ) = 3 x − 1 ( − ½ ) x − 3/2
p '( x ) = ( − 3/2) x − 5/2
مثال شماره 2 :
مشتق گناه (1 + x 2 ) را با استفاده از قانون زنجیره بیابید.
راه حل شماره 2 :
با استفاده از قانون زنجیره ای با n ( x ) = 1 + x ^2 و m ( x ) = sin x نتیجه می شود که
n '( x ) =2 x
و
m '[ n ( x )] = cos(1 + x^ 2 )
p '( x ) = m ' [ n ( x )] n ' ( x ) = cos(1 + x ^2 )2 x
p ' ( x ) = 2 x cos (1 + x^ 2 )
این آموزش به سه بخش تقسیم می شود؛ آن ها هستند:
به عبارت بسیار ساده، مشتق تابع f(x) نرخ تغییر آن را نشان میدهد و با f'(x) یا df/dx نشان داده میشود. بیایید ابتدا به تعریف آن و یک تصویر تصویری از مشتق نگاه کنیم.
تصویری از تعریف یک مشتق تابع
در شکل Δx نشان دهنده تغییر در مقدار x است. ما فاصله بین x و (x+Δx) را کوچکتر و کوچکتر می کنیم تا زمانی که بینهایت کوچک شود. بنابراین، ما محدودیت داریم (Δ𝑥 0). صورتگر f(x+Δx)-f(x) تغییر متناظر در مقدار تابع f را در بازه Δx نشان میدهد. این باعث می شود که مشتق تابع f در نقطه x، نرخ تغییر f در آن نقطه باشد.
نکته مهمی که باید به آن توجه داشت این است که Δx، تغییر x می تواند منفی یا مثبت باشد. از این رو:
0<|Δx|< 𝜖،
جایی که 𝜖 یک مقدار بی نهایت کوچک است.
مشتق یک تابع را می توان با f'(x) و df/dx نشان داد. نیوتن غول ریاضی از f'(x) برای نشان دادن مشتق یک تابع استفاده کرد. لایب نیتس، یکی دیگر از قهرمانان ریاضی، از df/dx استفاده کرد. بنابراین df/dx یک عبارت واحد است که نباید با کسری اشتباه گرفته شود. به عنوان مشتق تابع f نسبت به x خوانده می شود و همچنین نشان می دهد که x متغیر مستقل است.
یکی از متداولترین نمونههایی که از مشتقات ذکر شده، سرعت است. سرعت، میزان تغییر فاصله زمانی است. بنابراین اگر f(t) نشان دهنده مسافت طی شده در زمان t باشد، آنگاه f'(t) سرعت در زمان t است. بخش های زیر نمونه های مختلفی از محاسبه مشتق را نشان می دهد.
روش یافتن مشتق تابع را تمایز می گویند. در این بخش، خواهیم دید که چگونه می توان از تعریف مشتق برای یافتن مشتق توابع مختلف استفاده کرد. بعداً، وقتی با تعریف راحتتر شدید، میتوانید از قوانین تعریفشده برای مشتق گیری یک تابع استفاده کنید.
بیایید با یک مثال ساده از یک تابع خطی m(x) = 2x+5 شروع کنیم. میتوانیم ببینیم که m(x) با یک نرخ ثابت تغییر میکند. ما می توانیم این تابع را به صورت زیر مشتق گیری کنیم.
مشتق m(x) = 2x+5
شکل بالا نشان می دهد که تابع m(x) چگونه در حال تغییر است و همچنین نشان می دهد که مهم نیست کدام مقدار از x، نرخ تغییر m(x) را انتخاب می کنیم همیشه 2 باقی می ماند.
فرض کنید تابع g(x) را داریم: g(x) = x^2. شکل زیر نحوه محاسبه مشتق g(x) را نشان می دهد. همچنین نمودار تابع و مشتق آن در شکل وجود دارد.
مشتق g(x) = x^2
به عنوان g'(x) = 2x، بنابراین g'(0) = 0، g'(1) = 2، g'(2) = 4 و g'(-1) = -2، g'(-2) = -4
از شکل می بینیم که مقدار g(x) برای مقادیر منفی بزرگ x بسیار بزرگ است . وقتی x <0، افزایش x باعث کاهش g(x) و از این رو g'(x) < 0 برای x<0 می شود. نمودار برای x=0 مسطح می شود، جایی که مشتق یا نرخ تغییر g(x) صفر می شود. هنگامی که x> 0، g(x) با افزایش x به طور درجه دوم افزایش می یابد، و از این رو، مشتق نیز مثبت است.
فرض کنید تابع h(x) = 1/x را داریم. در زیر مشتق h(x) (برای x ≠0) و شکلی که مشتق را نشان می دهد نشان داده شده است. منحنی آبی نشان دهنده h(x) و منحنی قرمز مشتق مربوط به آن است.
مشتق h(x) = 1/x
برای مثال 3، تابع h(x) = 1/x در نقطه x=0 تعریف نشده است. بنابراین، مشتق آن نیز در x=0 تعریف نشده است. اگر تابعی در نقطه ای پیوسته نباشد، در آن نقطه مشتق ندارد. در زیر چند سناریو وجود دارد که در آن یک تابع قابل مشتق گیری نیست:
در زیر چند نمونه آورده شده است:
نمونه هایی از نقاطی که هیچ مشتقی در آنها وجود ندارد
جواب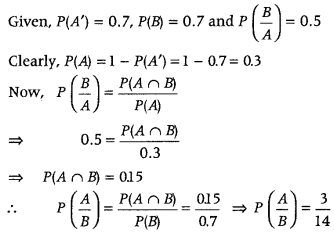
س

مثال 7
معادله مکعب زیر را حل کنید:
x ^3 + 3x^ 2 + x + 3 = 0.
راه حل
x^ 3 + 3x^ 2 + x + 3
= (x^ 3 + 3x ^2 ) + (x + 3)
= x ^2 (x + 3) + 1 (x + 3)
= (x + 3) (x^ 2 + 1)
بنابراین، x = i,-i, -3.
مثال 8
x^ 3 − 6x^ 2 + 11x − 6 = 0 را حل کنید
راه حل
تجزیه کنید
x^ 3 − 6x^ 2 + 11x − 6 = 0 ⟹ (x − 1) (x − 2) (x − 3) = 0
برابر کردن هر عامل با صفر به دست می دهد.
x = 1، x = 2 و x = 3
مثال 9
x^ 3 − 4x ^2 − 9x + 36 = 0 را حل کنید
راه حل
هر مجموعه از دو عبارت را تجزیه کنید.(روش دسته بندی)
x ^2 (x - 4) - 9 (x - 4) = 0
فاکتور مشترک (x − 4) را استخراج کنید تا به دست آید
(x ^2 − 9) (x − 4) = 0
حالا از اتحاد مزدوج تجزیه کنید
(x + 3) (x - 3) (x - 4) = 0
با برابر کردن هر عامل با صفر، به دست می آوریم؛
x = -3، 3 , 4
مثال 10
معادله 3x^ 3 −16x ^2 + 23x − 6 = 0 را حل کنید
راه حل
3x ^3 −16x^ 2 + 23x – 6 را بر x -2 تقسیم کنید تا 3x^ 2 – 1x – 9x + 3 بدست آورید
= x (3x – 1) – 3 (3x – 1)
= (x - 3) (3x - 1)
بنابراین،
3 x ^3 −16x^ 2 + 23x − 6 = (x- 2) (x – 3) (3x – 1)
هر عامل را با صفر برابر کنید تا به دست آورید
x = 2، 3 , 1/3
مثال 11
ریشه های 3x ^3 – 3x ^2 – 90x=0 را پیدا کنید
راه حل
فاکتور آن را 3 برابر کنید
3x^ 3 - 3x ^2 - 90x ⟹3x (x^ 2 - x - 30)
یک جفت عامل را پیدا کنید که حاصلضرب آنها 30- و مجموع آنها 1- باشد.
⟹- 6 * 5 = 30
⟹ −6 + 5 = -1
معادله را با جایگزینی عبارت "bx" با عوامل انتخاب شده بازنویسی کنید.
⟹ 3x [(x ^2 - 6x) + (5x - 30)]
عامل معادله؛
⟹ 3x [(x (x - 6) + 5 (x - 6)]
= 3x (x - 6) (x + 5)
با برابر کردن هر عامل با صفر، به دست می آوریم؛
x = 0، 6، -5
مساحتی که با اضلاع مستطیل محدود شده است، با داشتن مختصات رئوس آن در شکلی که نقطه B در مبدأ آن قرار دارد، محدود شده است؟
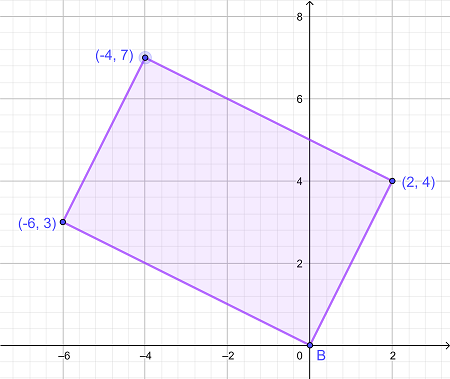 |
پاسخ به انتخاب ها
اگر مختصات راس B (2-، -15) و برای راس D (-3، -2) باشد ، مساحت مستطیل شکل زیر را بیابید .
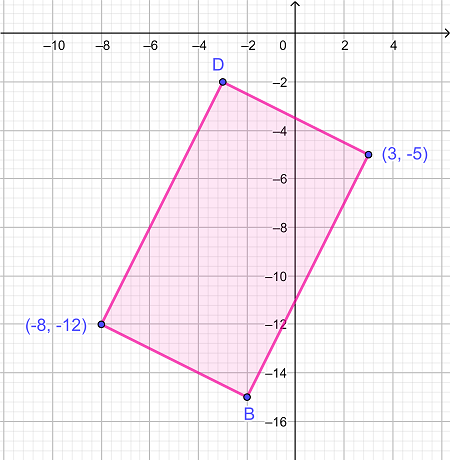 |
پاسخ صحیح را برای مساحت مستطیل زیر انتخاب کنید.
 |
اگر مختصات هر رأس به صورت زیر باشد، مساحت محدود شده با مستطیل زیر را تعیین کنید:
W = (-6، 1)
X = (-2، -2)
Y = (4، 6)
Z = (0، 9)
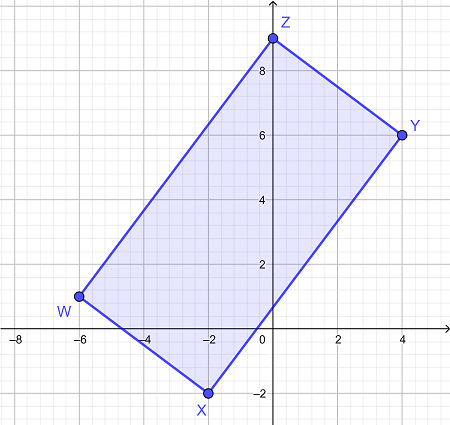 |
پاسخ به انتخاب ها
مساحت شکل مستطیلی که در شکل زیر نشان داده شده است چقدر است؟
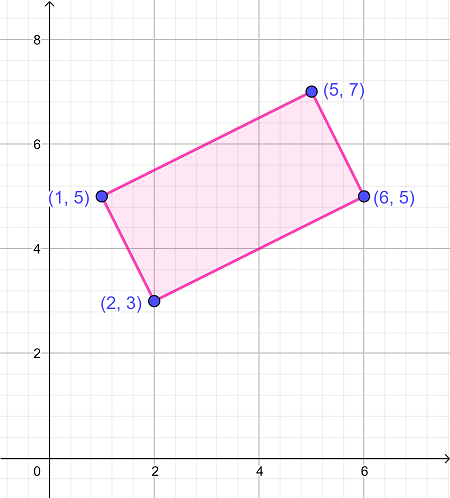 |
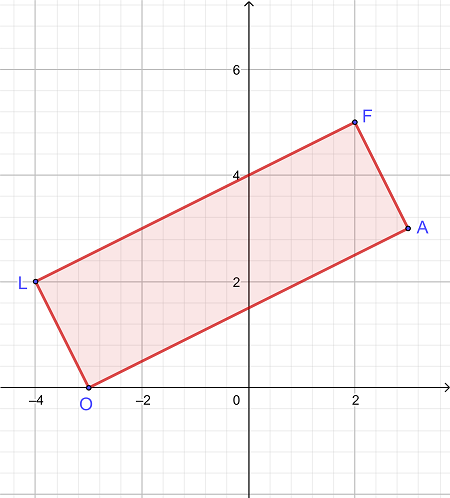
مساحت مستطیل LOAF را در یک صفحه مختصات در صورتی حل کنید که رئوس آن در مختصات زیر باشد:
L = (-4، 2)
O = (-3، 0)
A = (3، 3)
F = (2، 5)
 |
پاسخ به انتخاب ها
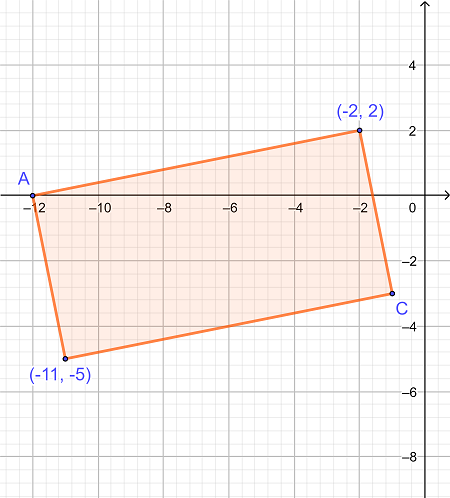
مساحت مستطیل را در صفحه مختصات دکارتی زیر محاسبه کنید اگر مختصات نقطه A و C به صورت زیر باشد:
A = (-12، 0)
C = (-1، -3)
 |
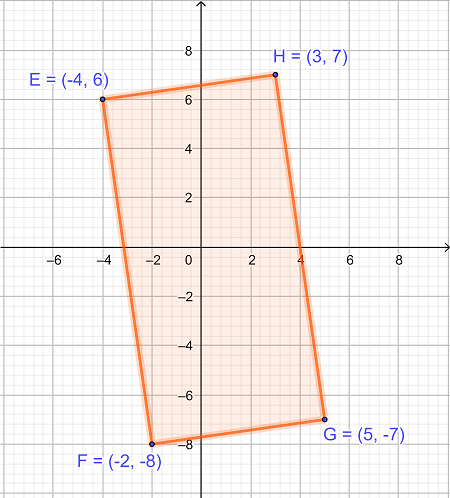
مساحت مستطیل در شکل داده شده را حل کنید.
 |
مساحت ناحیه سایهدار را که در شکل زیر نشان داده شده است، تعیین کنید.
 |
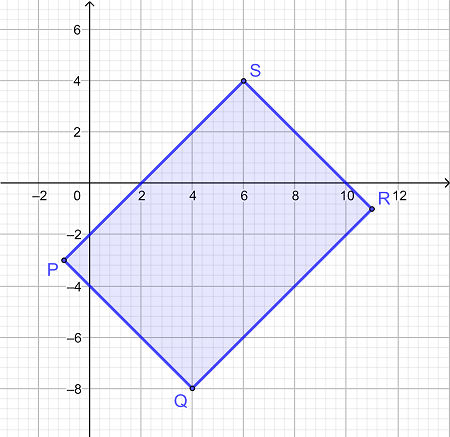
مساحت مستطیل را در شکل داده شده در صورتی تعیین کنید که رئوس آن به صورت زیر باشد:
P = (-1، -3)
Q = (4، -8)
R = (11, -1)
S = (6، 4)
 |
مساحت محدود شده با مستطیل TUVW زیر را محاسبه کنید.
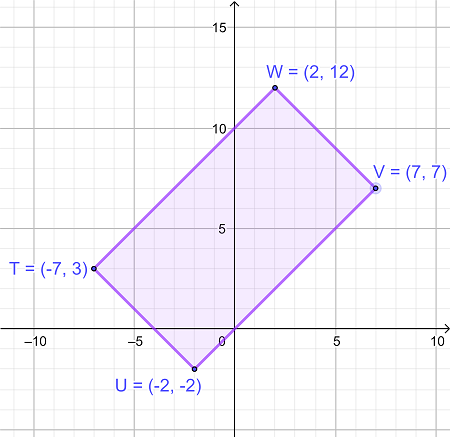 |
مساحت شکل مستطیلی در شکل زیر چقدر است؟
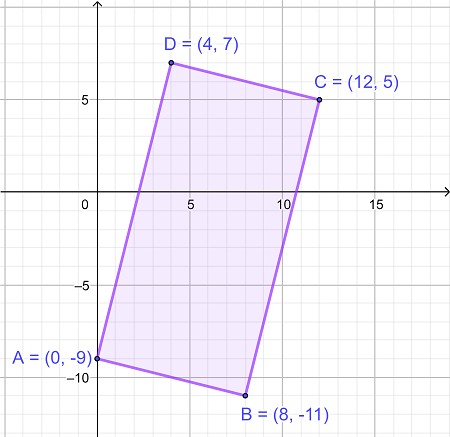 |
مساحت محدود شده توسط مستطیل را در صفحه مختصاتی که در شکل زیر نشان داده شده است محاسبه کنید.
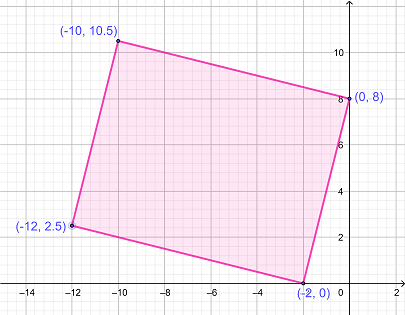 |
اگر مختصات نقطه A و C به ترتیب (8-, -2) و (0, -1) باشد مساحت مستطیل ABCD را تعیین کنید.
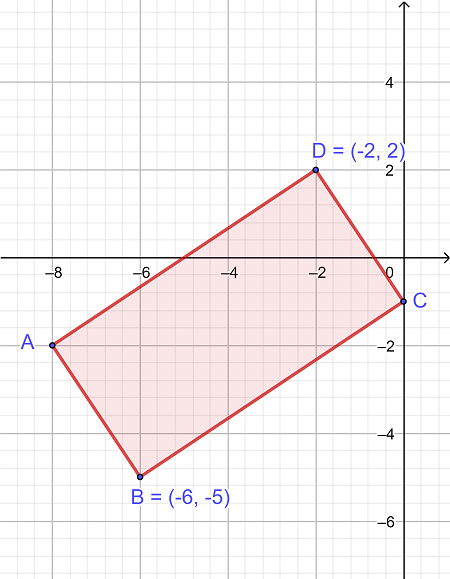 |
اگر مختصات هر رأس در زیر نشان داده شود، مساحت مستطیل در یک صفحه مختصات چقدر است؟
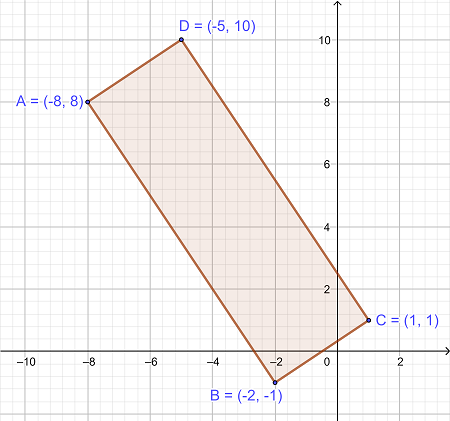 |
مساحت مستطیل ABCD را در صفحه مختصات تعیین کنید اگر رئوس به صورت زیر قرار گیرند:
A = (-5، -3)
B = (-1، -9)
C = (8، -3)
D = (4، 3)
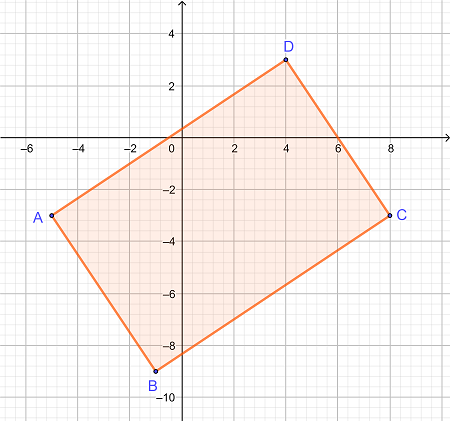 |
مقدار صحیح مساحت ناحیه سایه دار مستطیلی را همانطور که در شکل زیر نشان داده شده است، پیدا کنید.
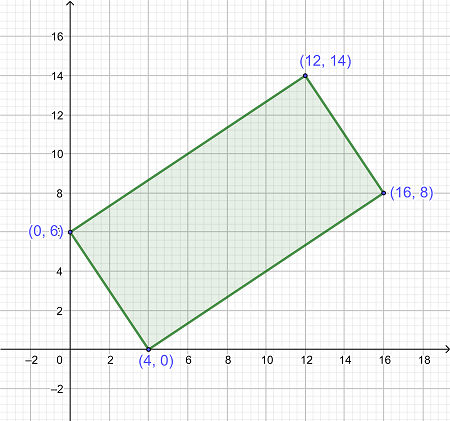 |
مساحت مستطیل داده شده را در صورتی محاسبه کنید که مختصات رئوس آن به صورت زیر باشد:
A = (-4، -6)
B = (11، -16)
C = (15، -10)
D = (0، 0)
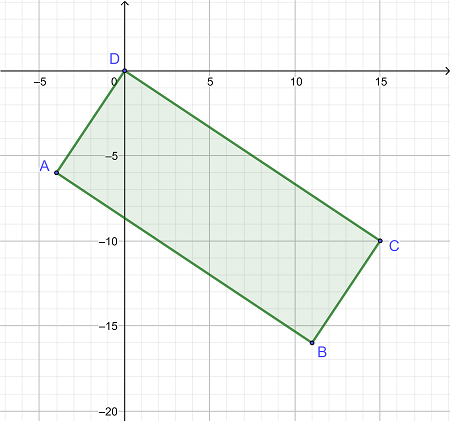 |
پاسخ به انتخاب ها
مساحت محصور در شکل مستطیلی در شکل چقدر است؟
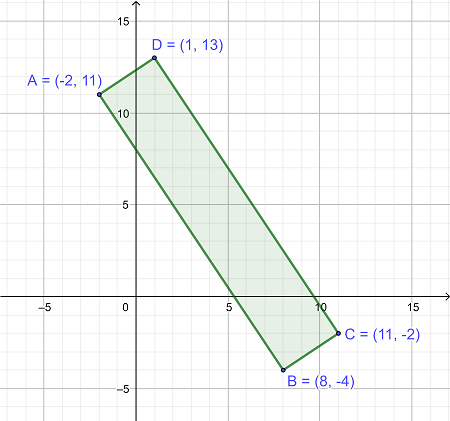 |
اگر مختصات نقطه M (3-، 18) و نقطه K (2-، 1) باشد، مساحت مستطیل زیر را پیدا کنید.
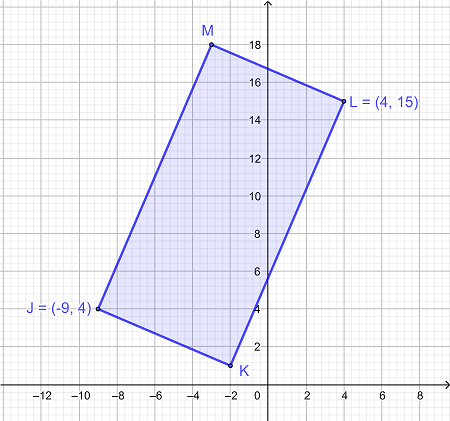 |
مساحت محدود شده با مستطیل ABCD را مطابق شکل زیر حل کنید.
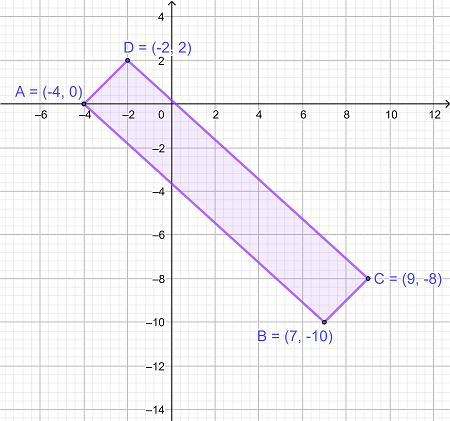 |
مختصات رئوس P، Q، R و S به ترتیب (-13، -13)، (-7، -17)، (5، 1) و (-1، 5) است. مساحت مستطیل تشکیل شده توسط آن مختصات را تعیین کنید.
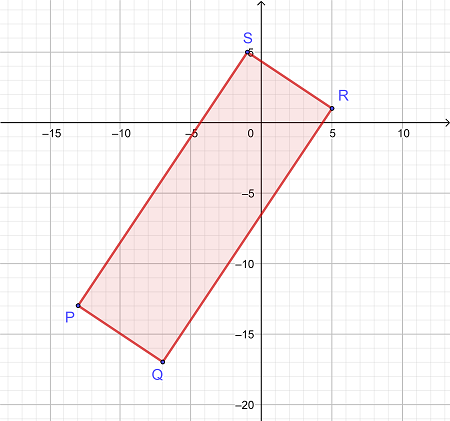 |
 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.