​

انتگرال "به روش جزء به جزء" بر اساس اتحادی است که می تواند به عنوان مثال به صورت زیر بیان شود:

( برای سایر احتمالات و اطلاعات بیشتر به انتگرال جزء به جزء در نظریه - روش های انتگرال مراجعه کنید.) ایده اصلی این روش به شرح زیر است: به شما یک انتگرال داده می شود و موفق می شوید آن را با انتگرال سمت چپ در اتحادفوق مطابقت دهید. سپس می توانید به عبارت سمت راست منتقل شوید. البته، انجام این کار تنها در صورتی منطقی است که انتگرال جدید در سمت راست آسان‌تر باشد (یا همان را در زیر ببینید).

الگوریتم انتگرال به روش جزء به جزءمرحله 1. تابع یکپارچه را به عنوان حاصل ضرب دو عبارت بیان کنید. یکی از آنها را f ( x ) و دیگری را g ′( x ) نشان دهید.مرحله 2. دو عبارت دیگر که در فرمول ظاهر می شوند را تعیین کنید. یعنی f ′( x ) با افتراق عبارت f ( x ) به دست می آید. g ( x ) با انتگرال g ′( x ) به دست می آید، جایی که + C استفاده نمی شود.مرحله 3.آن عبارت را به فرمول by part وصل کنید. این روند به پایان می رسد و اکنون می توانید سعی کنید انتگرال جدید را در سمت راست ارزیابی کنید.

سنتی است که استفاده از انتگرال به روش جزء به جزء را در یک ماتریس علامت گذاری می کنیم، f و g را در ردیف اول قرار می دهیم و f و g را در ردیف دوم محاسبه می کنیم. اکنون یک مثال نشان خواهیم داد.

توجه داشته باشید که کل عبارت در انتگرال داده شده باید در رویه گنجانده شود، بنابراین وقتی دو عبارت را در ردیف اول ماتریس ضرب می کنیم، باید دقیقاً عبارت انتگرال را بدست آوریم. امکان کنار گذاشتن بخشی از انتگرال داده شده وجود ندارد. همانطور که می بینیم، در ردیف دوم ماتریس، انتگرال جدید را پیدا می کنیم.

انتگرال‌های باتجربه گاهی این ماتریس را نمی‌نویسند، انتگرال بر اساس قطعات به این صورت است: ابتدا بخشی از عبارت داده شده را انتگرال می‌کنید و بنابراین اولین عبارت جدید را دریافت می‌کنید، عبارتی که قبلا انجام شده است. در این عبارت جدید، نیمه دیگر را متمایز می کنید و انتگرال جدید را دریافت می کنید.

نحوه انتخاب انتگرال بر اساس قطعات

دو چیز وجود دارد که باید در نظر گرفت. اول، قسمتی که قصد داریم آن را انتگرال کنیم، یعنی آن چیزی که برای g ′( x ) انتخاب کردیم، بهتر است فوراً بتوانیم آن را انتگرال کنیم (انتگرال پیچیده برای g به ندرت منجر به انتگرال بهبود یافته می شود). این ما را به شدت محدود می‌کند، اساساً به قدرت‌ها، سینوس‌ها و کسینوس‌ها، و نمایی بستگی دارد. در واقع هیچ چیز دیگری وجود ندارد که بتوانیم در پرواز انتگرال کنیم.ثانیاً بقیه، یعنی بخشی که قصد داریم آن را متمایز و با f نشان دهیم، باید در هنگام متمایز شدن به طور قابل توجهی بهتر شود (دقیقا اینجاست که باید مطمئن شویم که انتگرال جدید ساده تر خواهد بود). دوباره، وقتی مشتقات عبارات مختلف را تصور می کنیم، متوجه می شویم که در اینجا نیز انتخاب زیادی نداریم.

وقتی آن را کنار هم می گذاریم، اساساً به سه نوع انتگرال می رسیم که در آن اعمال یکپارچگی به روش جزء به جزء منطقی است. بهتر است آنها را به خاطر بسپارید.

• نوع " حذف x ".یک انتگرالی از این نوع را در ابتدای این بخش دیدیم، در محصول تابعی داریم که به راحتی در یک چند جمله ای ضرب می شود که با استفاده از تمایز آن را کاهش می دهیم. مثال های اساسی:

ما توان x (یا به طور کلی یک چند جمله ای) را f و آن تابع به راحتی قابل انتگرال را g ′ می گیریم. بدیهی است که هر تمایز یک درجه از چند جمله ای را کاهش می دهد، بنابراین اگر زمانی که توان بالاتری وجود دارد، انتگرال به روش جزء به جزء باید تکرار شود. اکنون مثال جالب تری را نشان خواهیم داد. ابتدا یک محاسبه تکمیلی انجام می دهیم، یک انتگرالگر با تجربه این کار را در حین انتگرال به روش جزء به جزء انجام می دهد.

اکنون می‌توانیم انتگرال زیر را ارزیابی کنیم، یک نامزد واضح برای حذف x با استفاده از انتگرال به روش جزء به جزء.

یکی از رایج ترین اشتباهات یکپارچه سازی فراموش کردن براکت ها هنگام تکرار انتگرال به روش جزء به جزء است. توجه داشته باشید که اگر توان x دارای توانی برابر با یک عدد صحیح مثبت نباشد، این روش کمکی نخواهد کرد. خودتان را متقاعد کنید که برای مثال نمی توانید با تمایز از شر جذر x خلاص شوید .

• نوع " حذف لگاریتم ".این رویکرد مبتنی بر این مشاهدات است که با تفکیک یک لگاریتم یک توان دریافت می‌کنیم، بنابراین انتگرال جدید اصلاً بدون لگاریتم خواهد بود. ما از این رویکرد برای انتگرال هایی مانند استفاده می کنیم

در اینجا این کار را برعکس انجام می دهیم، توان لگاریتم را f و توان x (یا چند جمله ای) را g ′ می گیریم. قدرت های بالاتر لگاریتم نیاز به انتگرال مکرر به روش جزء به جزء دارد.

مورد توجه ویژه آخرین انتگرال است. احتمالاً قبلاً متوجه شده اید که لگاریتم به طور مشکوکی در جدول انتگرال های ابتدایی وجود ندارد. دلیل واضح است، لگاریتم مشتق هیچ تابع ابتدایی نیست و انتگرال آن معمولاً با استفاده از انتگرال به روش جزء به جزء و انتخاب کنجکاو (و روی حیله) g ′ = 1 ارزیابی می شود (مگر اینکه آن را به خاطر بسپاریم یا جایی پیدا کنیم ) .

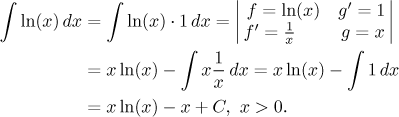
• نوع " حذف توابع مثلثاتی معکوس ".توابع مثلثاتی معکوس شبیه لگاریتم هستند زیرا مشتقات آنها از نوع کاملاً متفاوت و از نظر انتگرال بسیار بهتر هستند. بنابراین می توان ترفند مشابهی را برای انتگرال هایی مانند موارد زیر اعمال کرد:

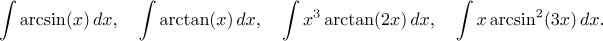
به عنوان مثال، انتگرال مهم مماس قوس را نشان خواهیم داد، جایی که ما دوباره از ترفند 1 استفاده می کنیم.

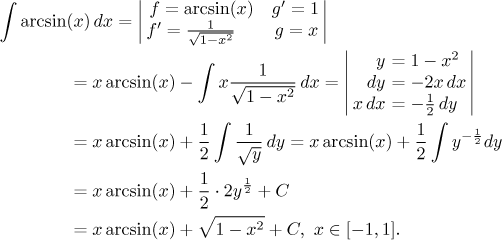
خواننده اغلب در ارتباط با سه نوع ذکر شده در بالا با قطعات انتگرال می شود، اما این روش می تواند در موقعیت های دیگر نیز استفاده شود، گاهی اوقات به روشی شگفت انگیز. اکنون یک ترفند بسیار مفید را نشان خواهیم داد.

ترفند با یک معادله:ما از این ترفند برای مسائلی استفاده می کنیم که در آن، پس از (چندین) محاسبه «بر اساس بخش»، همان انتگرالی را که با آن شروع کردیم، فقط با علامت مخالف به دست می آوریم. این به بهترین شکل با یک مثال توضیح داده می شود:

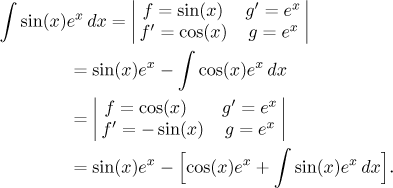
یک معادله می گیریم

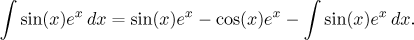
اگر انتگرال سمت راست را به سمت چپ منتقل کنیم (با توجه به اینکه این دو مجموعه از پاد مشتق هستند، بنابراین ممکن است با یک ثابت تفاوت داشته باشند و این ثابت در سمت راست باقی بماند)، به دست می‌آییم.

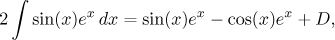
و از این رو

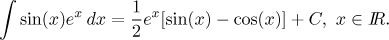
(ما C = D /2 ​​را نشان می‌دهیم. اگر D مقداری ثابت (خودسرانه) باشد، برای D /2 ​​نیز همینطور است ، بنابراین می‌توانیم آن را با یک حرف نشان دهیم.)

این نوع خاص از انتگرال نیز در برخی از برنامه ها بسیار مفید است و نتیجه ای که ما به دست آوردیم را می توان در لیست های گسترده تری از انتگرال ها یافت. دو حالت دیگر با معادلات در این مسئله و این مسئله در حل المسائل - انتگرالها یافت می شود .

نکته: توجه داشته باشید که لازم نیست پاد مشتق که برای g می گیریم ساده ترین باشد، با C به عنوان 0 در نظر گرفته می شود. گاهی اوقات ممکن است به نفع ما باشد که از یک مقدار متفاوت برای کمک به ما در انتگرال جدید استفاده کنیم. مشکل زیر را در نظر بگیرید. این یک نمونه معمولی از نوع "حذف لگاریتم" است و ما یکپارچه سازی قطعات را به روش معمول اعمال می کنیم.

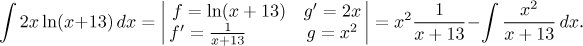
برای پایان دادن به مسئله، ابتدا باید چند جمله ای را تقسیم کرده و سپس باقیمانده را انتگرال کنیم، که دشوار نیست، اما اگر مجبور نیستیم چرا کار کنیم. یک ترفند ساده ما را از شر آن کسری خلاص می کند.

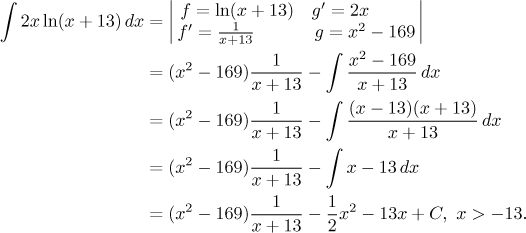
خیلی بهتر. این اغلب آنقدر اتفاق نمی افتد که زمان زیادی را صرف آن کنیم، اما خوب است که از این واقعیت آگاه باشیم که در واقع مقداری آزادی در انتخاب g وجود دارد .

انتگرال به روش جزء به جزء نیز پشت برخی از فرمول های مفید است، این یادداشت و این یادداشت را ببینید . همانطور که دیدیم، انتگرال به روش جزء به جزء، انتگرال هایی از چندین تابع اساسی را به دست می دهد، بنابراین روش بسیار مهمی است. استفاده معمولی از آن را می توان در این مسئله ، این مشکل و این مشکل در حل مسائل - انتگرال یافت .

منبع

https://math.fel.cvut.cz/mt/txtd/3/txe3db3c.htm

​