برای شمارش تعداد عناصر در اجتماع دو مجموعه (A و B)، باید تعداد آیتم های مجموعه A، تعداد آیتم های مجموعه B و تعداد آیتم های هر دو A و B را بدانیم. (اشتراک الف و ب).
صرف جمع کردن عناصر A و B با یکدیگر، عناصر موجود در اشتراک را دو بار میشماریم، بنابراین برای بدست آوردن تعداد صحیح عناصر در اجتماع A و B، باید محل اشتراک A و B را کم کنیم. با استفاده از فرمول ریاضی زیر بیان شده است:

راه دیگر برای نگاه کردن به این مفهوم استفاده از نمودار ون یا نمایش بصری مجموعه ها است. در شکل 1 زیر، دایره سمت چپ نشان دهنده مجموعه A، دایره سمت راست مجموعه B، و همپوشانی نشان دهنده اشتراک A و B است. هر چیزی که در هر دو دایره باشد نشان دهنده اجتماع A و B است. هر دو دایره، باید کم شود تا فقط یک بار شمارش شود. توجه داشته باشید که جهان U شامل همه چیز در کل جعبه است.
شکل 1: نمودار ون با دو مجموعه

برای باز کردن قفل این درس باید عضو Study.com باشید. حساب کاربری برای خود بسازید
گنجاندن-خروج با سه مجموعه
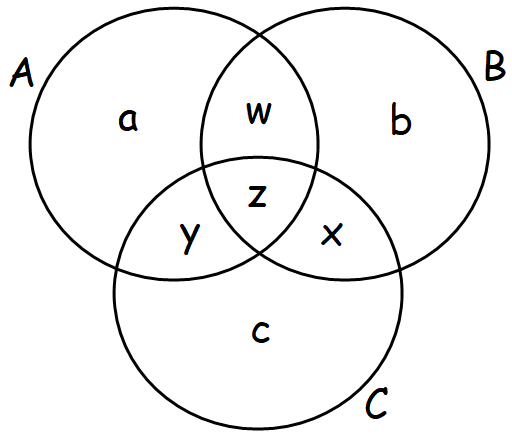
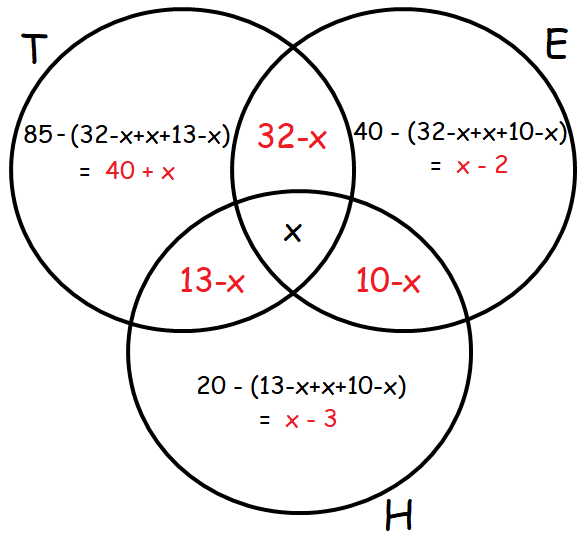
اکنون که با دو مجموعه تمرین کرده ایم، بیایید نحوه شمارش عناصر شامل سه مجموعه (A، B و C) را در نظر بگیریم. اگر تعداد عناصر هر یک از سه مجموعه را اضافه کنیم، دوباره عناصری را که در بیش از یک مجموعه قرار دارند، چندین بار می شماریم، همانطور که در شکل 2 زیر نشان داده شده است. مناطقی که دو مجموعه با هم تداخل دارند دو بار و منطقه ای که هر سه مجموعه با هم همپوشانی دارند سه بار شمارش می شود.
شکل 2: نمودار ون با سه مجموعه و تعداد منطقه

اگر هر یک از جفتها را کم کنیم، فرمول به شکل زیر است:

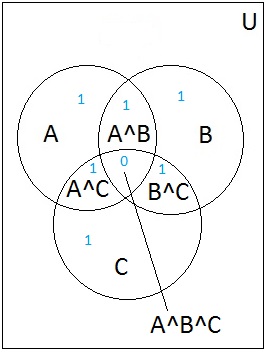
مشکل این روش این است که ناحیه وسطی که هر سه مجموعه در آن تلاقی می کنند به هیچ وجه شمارش نمی شود. این در شکل 3 نشان داده شده است.
شکل 3: نمودار ون با سه مجموعه و تعداد منطقه تنظیم شده است
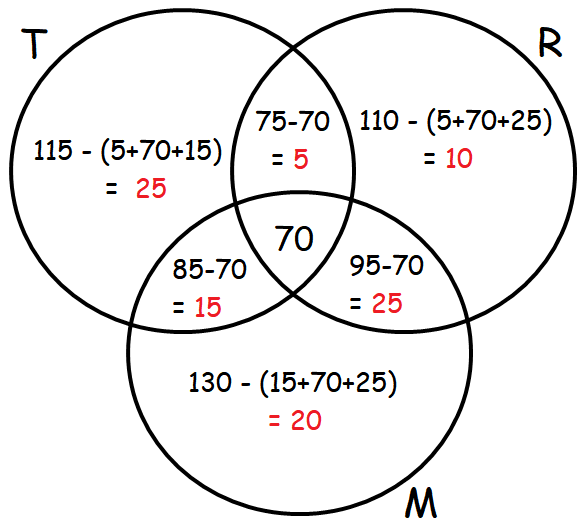
برای رفع این مشکل، به سادگی میتوانیم اشتراک هر سه مجموعه را دوباره به داخل اضافه کنیم، به طوری که فرمول اکنون به شکل زیر در میآید:
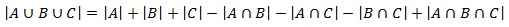
فرمول کلی شمول و عدم شمول
اصل شمول و عدم شمول را می توان به هر تعداد مجموعه n تعمیم داد ، که در آن n یک عدد صحیح مثبت است. اصل کلی شمول و عدم شمول به شرح زیر تعریف می شود:
بگذارید A 1 , A 2 , …, A n مجموعه های متناهی باشند. سپس

به عنوان مثال، اعمال این فرمول برای چهار مجموعه نتیجه می دهد:

خلاصه درس
این درس اصل
برای شمارش تعداد عناصر در اجتماع دو مجموعه (A و B)، باید تعداد آیتم های مجموعه A، تعداد آیتم های مجموعه B و تعداد آیتم های هر دو A و B را بدانیم. (اشتراک الف و ب).
صرف جمع کردن عناصر A و B با یکدیگر، عناصر موجود در اشتراک را دو بار میشماریم، بنابراین برای بدست آوردن تعداد صحیح عناصر در اجتماع A و B، باید محل اشتراک A و B را کم کنیم. با استفاده از فرمول ریاضی زیر بیان شده است:

راه دیگر برای نگاه کردن به این مفهوم استفاده از نمودار ون یا نمایش بصری مجموعه ها است. در شکل 1 زیر، دایره سمت چپ نشان دهنده مجموعه A، دایره سمت راست مجموعه B، و همپوشانی نشان دهنده اشتراک A و B است. هر چیزی که در هر دو دایره باشد نشان دهنده اجتماع A و B است. هر دو دایره، باید کم شود تا فقط یک بار شمارش شود. توجه داشته باشید که جهان U شامل همه چیز در کل جعبه است.
شکل 1: نمودار ون با دو مجموعه

برای باز کردن قفل این درس باید عضو Study.com باشید. حساب کاربری برای خود بسازید
گنجاندن-خروج با سه مجموعه
اکنون که با دو مجموعه تمرین کرده ایم، بیایید نحوه شمارش عناصر شامل سه مجموعه (A، B و C) را در نظر بگیریم. اگر تعداد عناصر هر یک از سه مجموعه را اضافه کنیم، دوباره عناصری را که در بیش از یک مجموعه قرار دارند، چندین بار می شماریم، همانطور که در شکل 2 زیر نشان داده شده است. مناطقی که دو مجموعه با هم تداخل دارند دو بار و منطقه ای که هر سه مجموعه با هم همپوشانی دارند سه بار شمارش می شود.
شکل 2: نمودار ون با سه مجموعه و تعداد منطقه

اگر هر یک از جفتها را کم کنیم، فرمول به شکل زیر است:

مشکل این روش این است که ناحیه وسطی که هر سه مجموعه در آن تلاقی می کنند به هیچ وجه شمارش نمی شود. این در شکل 3 نشان داده شده است.
شکل 3: نمودار ون با سه مجموعه و تعداد منطقه تنظیم شده است

برای رفع این مشکل، به سادگی میتوانیم اشتراک هر سه مجموعه را دوباره به داخل اضافه کنیم، به طوری که فرمول اکنون به شکل زیر در میآید:
فرمول کلی شمول و عدم شمول
اصل شمول و عدم شمول را می توان به هر تعداد مجموعه n تعمیم داد ، که در آن n یک عدد صحیح مثبت است. اصل کلی شمول و عدم شمول به شرح زیر تعریف می شود:
بگذارید A 1 , A 2 , …, A n مجموعه های متناهی باشند. سپس

به عنوان مثال، اعمال این فرمول برای چهار مجموعه نتیجه می دهد:

خلاصه درس
این درس اصل گنجاندن-حذف را پوشش میدهد که میتوان از آن برای شمارش تعداد آیتمهای درون مجموعههایی که موارد مشترک دارند، استفاده کرد. ما با مفاهیم بنیادی تئوری مجموعهها ، از جمله اجتماع و اشتراک ، که برای حل مسائل شمارش با استفاده از اصل شمول - طرد ضروری هستند، شروع کردیم. سپس فرمولها و مثالهای هر کدام، از جمله نمونههای دو مجموعه و سه مجموعه را بررسی کردیم. در نهایت، ما یک فرمول کلی برای اصل گنجاندن-خروج اعمال شده برای n مجموعه ارائه کردیم.
را پوشش میدهد که میتوان از آن برای شمارش تعداد آیتمهای درون مجموعههایی که موارد مشترک دارند، استفاده کرد. ما با مفاهیم بنیادی تئوری مجموعهها ، از جمله اجتماع و اشتراک ، که برای حل مسائل شمارش با استفاده از اصل شمول - طرد ضروری هستند، شروع کردیم. سپس فرمولها و مثالهای هر کدام، از جمله نمونههای دو مجموعه و سه مجموعه را بررسی کردیم. در نهایت، ما یک فرمول کلی برای اصل گنجاندن-خروج اعمال شده برای n مجموعه ارائه کردیم.









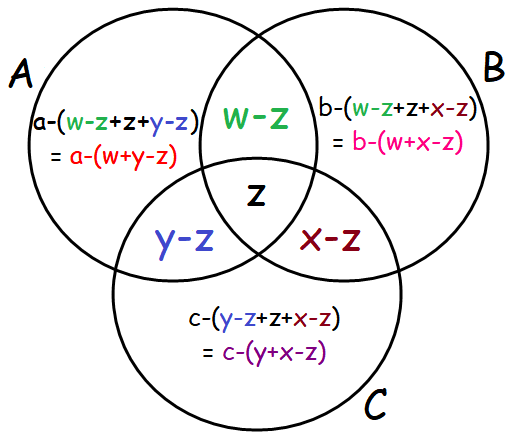
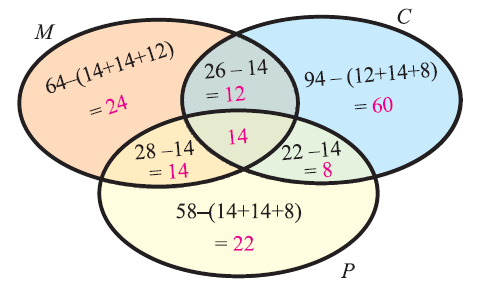
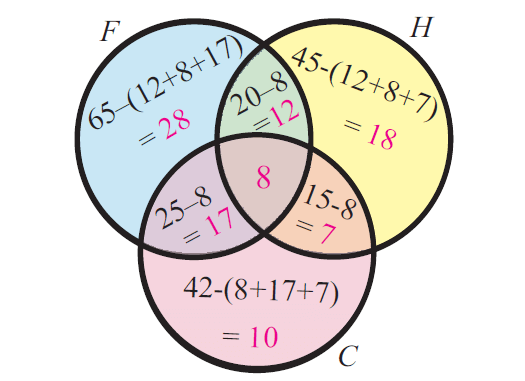
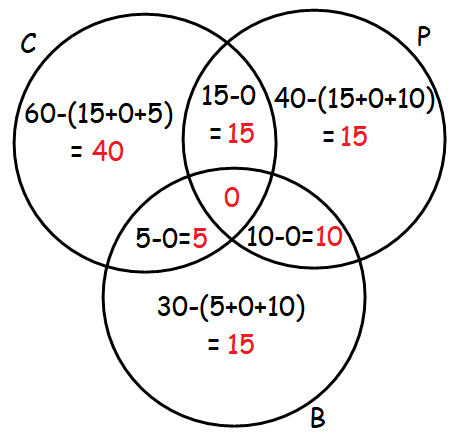

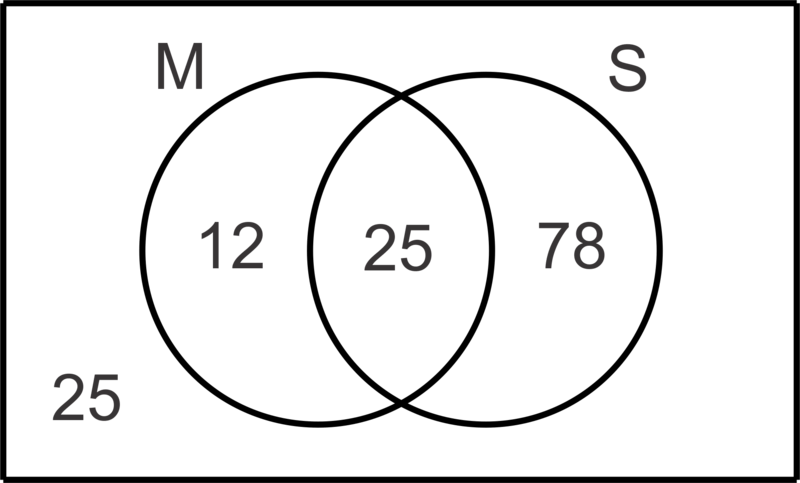




 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.