دل نوشته ها ی نقش و آموزش ریاضی  

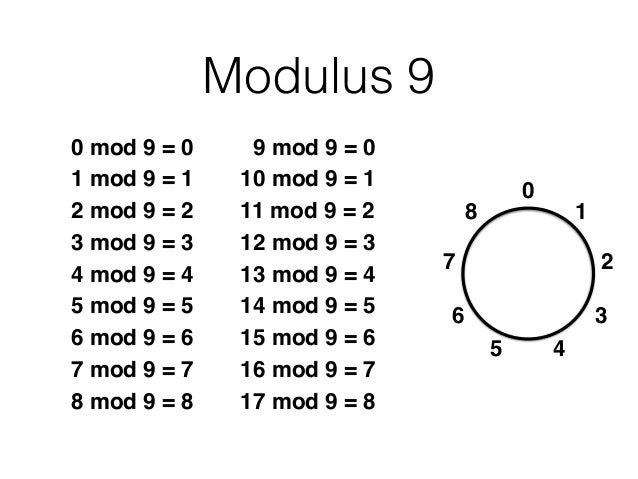
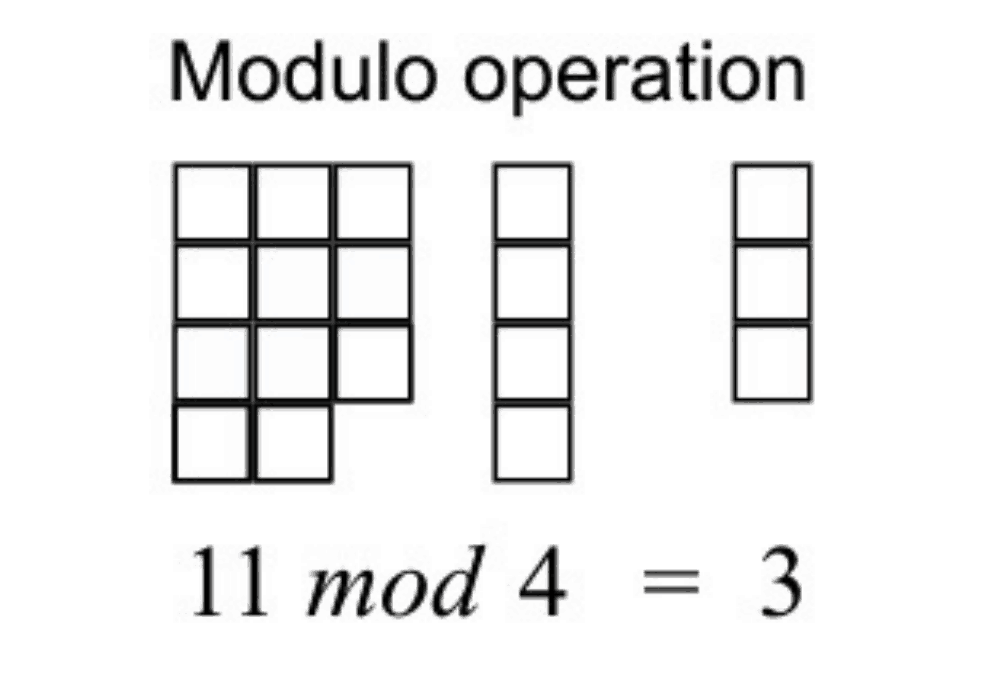
نقشه Königsberg در زمان اویلر که نشانگر چیدمان واقعی هفت پل است ، برجسته رودخانه Pregel و پل ها

پلهای کونیکسبرگ یک مشکل تاریخی قابل توجه در ریاضیات است. وضوح منفی آن توسط لئونارد اویلر در سال 1736 [1] مبانی نظریه گراف را پایه گذاری کرد و ایده توپولوژی را ترجیح داد . [2]

این شهرستان از Königsberg به در پروس (در حال حاضر کالینینگراد ، روسیه ) در هر دو طرف بر پا شد رودخانه Pregel ، و شامل دو بزرگ islands- Kneiphof و Lomse -که به یکدیگر متصل می شوند، و یا به این دو بخش از سرزمین اصلی شهرستان، توسط هفت پل مشکل این بود که یک پیاده روی در سطح شهر طراحی کنیم که هر یک از آن پلها یک بار و فقط یک بار عبور کند.

از طريق مشخص كردن كار منطقي به طور واضح و مشخص ، راه حل هاي مربوط به آن نيز وجود دارد

1. رسیدن به جزیره یا سرزمین اصلی به غیر از طریق یکی از پل ها ، یا
2. دسترسی به هر پل بدون عبور از انتهای دیگر آن

صریحاً غیرقابل قبول هستند

اویلر ثابت کرد که این مشکل هیچ راه حلی ندارد. مشکلی که وی با آن روبرو بود توسعه یک تکنیک مناسب برای تجزیه و تحلیل و آزمایش های بعدی بود که این ادعا را با دقت ریاضی برقرار کرد.

فهرست

• 1تحلیل اویلر
• 2اهمیت در تاریخ و فلسفه ریاضیات
• 3وضعیت فعلی پل ها
• 4همچنین ببینید
• 5منابع
• 6لینک های خارجی

تجزیه و تحلیل اویلر [ ویرایش ]

اول ، اویلر اظهار داشت که انتخاب مسیر داخل هر توده زمین بی ربط نیست. تنها ویژگی مهم یک مسیر ، توالی پل های عبور شده است. این به او امکان می داد تا مسئله را به صورت انتزاعی (ایجاد مبانی نظریه گراف ) بازسازی کند و کلیه ویژگی ها را به جز لیست توده های زمین و پل های اتصال آنها حذف کند. در اصطلاح مدرن ، هر كدام از توده هاي زمين را با يك " راس " يا گره انتزاعي جايگزين مي كنند ، و هر پل با يك اتصال انتزاعي ، يك " لبه " ، كه فقط براي ثبت اينكه چه جفتي از راس ها (توده هاي زميني) با آن پل متصل هستند ، تعيين مي شود. ساختار ریاضی حاصل نمودار است .

→ → 

از آنجا که فقط اطلاعات اتصال مرتبط است ، ممکن است شکل بازنمایی های تصویری یک نمودار به هیچ وجه تحریف شود ، بدون اینکه خود نمودار تغییر کند. فقط وجود (یا عدم) لبه بین هر جفت گره قابل توجه است. به عنوان مثال ، فرقی نمی کند که لبه های کشیده شده صاف یا خمیده باشند یا اینکه یک گره در سمت چپ یا راست دیگری باشد.

بعد ، اویلر مشاهده کرد که (به جز در نقاط پایانی پیاده روی) ، هر گاه شخصی توسط یک پل وارد یک راس شود ، یکی از راسها توسط یک پل خارج می شود. به عبارت دیگر ، در حین هر پیاده روی در نمودار ، تعداد دفعاتی که شخص وارد یک راس غیر ترمینال می کند برابر است با تعداد دفعاتی که یکی از آن خارج می شود. حال اگر هر پل دقیقاً یک بار طی شده باشد ، نتیجه می گیرد که برای هر توده زمین (به جز آنهایی که برای شروع و پایان انتخاب شده اند) ، تعداد پل های لمس شده بر آن جرم زمین باید حتی (نیمی از آنها) در خاص گذرگاه ، خواهد شد "به سمت" سرزمین ماساژ؛ نیمه دیگر ، "دور" از آن). با این حال ، هر چهار توده زمین در مشکل اصلی با یک چیز عجیب روبرو هستندتعداد پل ها (یکی با 5 پل لمس می شود ، و 3 مورد دیگر با 3 لمس می شوند). از آنجا که ، حداکثر ، دو توده زمین می توانند به عنوان نقاط پایانی یک پیاده روی خدمت کنند ، پیشنهاد پیاده روی که از هر پل یک بار عبور می کند یک بار منجر به تضاد می شود.

در زبان مدرن ، اویلر نشان می دهد که احتمال قدم زدن در یک نمودار ، که هر لبه را دقیقاً یک بار طی می کند ، بستگی به درجه گره ها دارد. درجه گره تعداد لبه های لمس آن است. استدلال اویلر نشان می دهد که شرط لازم برای پیاده روی فرم مورد نظر این است که نمودار به هم متصل شده و دقیقاً صفر یا دو گره از درجه عجیب و غریب داشته باشد. این شرایط همچنین کافی است - نتیجه ای که توسط اویلر بیان شد و بعدا توسط کارل هیرولزر اثبات شد . چنین پیاده روی اکنون یک مسیر اویلری یا پیاده روی اویلر نامیده می شودبه افتخار او علاوه بر این ، اگر گره هایی با درجه عجیب و غریب وجود داشته باشد ، آنگاه هر مسیر اویلری در یکی از آنها شروع می شود و در دیگری خاتمه می یابد. از آنجا که نمودار مربوط به K correspondingnigsberg تاریخی دارای چهار گره از درجه عجیب و غریب است ، نمی تواند یک مسیر اویلری داشته باشد.

یک شکل جایگزین از مسیری می خواهد که مسیری را طی کند که تمام پل ها را طی کند و همچنین دارای نقطه شروع و پایان یکسان باشد. چنین پیاده روی را مدار اویلری یا تور اویلر می نامند . چنین مدار در صورتی وجود دارد که ، و فقط در صورت اتصال ، نمودار متصل شود ، و به هیچ وجه هیچ گره ای از درجه عجیب و غریب وجود ندارد. تمام مدارهای اویلری نیز مسیرهای اویلری هستند ، اما همه مسیرهای اویلری مدارهای اویلری نیستند.

کار اویلر در 26 آگوست 1735 به آکادمی سن پترزبورگ ارائه شد و به عنوان Solutio problematis ad geometriam situs pertinentis (حل مسئله مربوط به هندسه موقعیت) در مجله Commentsarii Academiae shkenciarum Petropolitanae در 1741 منتشر شد. [3] این کتاب به زبان انگلیسی در دنیای ریاضیات موجود است .

اهمیت در تاریخ و فلسفه ریاضیات [ ویرایش ]

در تاریخ ریاضیات ، حل اویلر از مشکل پل K bridgenigsberg به عنوان اولین قضیه نظریه گراف و اولین اثبات واقعی در نظریه شبکه ها ، [4] موضوعی که اکنون عموماً به عنوان شاخه ای از ترکیبات در نظر گرفته می شود . مشکلات ترکیبی انواع دیگر از زمان باستان در نظر گرفته شده بود.

علاوه بر این ، تشخیص اویلر مبنی بر اینکه اطلاعات کلیدی تعداد پل ها بوده و لیست نقاط پایانی آنها (به جای موقعیت دقیق آنها) توسعه توپولوژی را حفظ می کند . تفاوت بین طرح واقعی و نمودار شماتیک نمونه خوبی از این ایده است که توپولوژی به شکل سفت و سخت اشیاء مربوط نمی شود.

از این رو ، همانطور که اویلر تشخیص داد ، "هندسه موقعیت" در مورد "اندازه گیری ها و محاسبات" نیست بلکه درباره چیز کلی تر است. این دیدگاه سنتی ارسطویی را زیر سوال می برد که ریاضیات "علم کمیت " است. گرچه این نمای متناسب با هندسه حساب و اقلیدسی است ، اما از نظر توپولوژی و ویژگیهای ساختاری انتزاعی تر مورد مطالعه در ریاضیات مدرن قرار نمی گرفت. [ نیاز به استناد ]

فیلسوفان خاطرنشان كردند كه اثبات اویلر مربوط به انتزاع یا الگویی از واقعیت نیست ، بلكه مستقیماً در مورد ترتیب واقعی پل ها است. از این رو ، قطعیت اثبات ریاضی می تواند به طور مستقیم در واقعیت صدق کند. [5]

حالت فعلی پلها [ ویرایش ]

نقشه مدرن کالینینگراد. مکان های باقی مانده از پل ها به رنگ سبز برجسته هستند ، در حالی که آنهایی که نابود شده اند به رنگ قرمز برجسته هستند.

دو تا از هفت پل اصلی از بمباران كونیگزبرگ در جنگ جهانی دوم زنده نماند . دو نفر دیگر بعداً تخریب و جایگزین بزرگراه مدرن شدند. سه پل دیگر باقی مانده است ، اگرچه تنها دو مورد از زمان اویلر (یکی در سال 1935 بازسازی شد). [6] بنابراین ، از سال 2000 ، پنج پل در همان سایت هایی که در مشکل اویلر نقش داشتند ، وجود دارند.

از نظر تئوری نمودار ، دو گره اکنون دارای درجه 2 و دو مورد دیگر دارای درجه 3 هستند. بنابراین ، یک مسیر اویلری اکنون امکان پذیر است ، اما باید در یک جزیره آغاز شود و از طرف دیگر پایان یابد. [7]

دانشگاه کانتربری در کرایستچرچ یک مدل از پل را به یک منطقه چمن بین فیزیکی کتابخانه علوم قدیمی و ساختمان ارسکین گنجانیده شده است، مسکن گروه ریاضی، آمار و علوم کامپیوتر. [8] رودخانه با بوته کوتاه و ورزشی جزیره مرکزی سنگ جایگزین تورو . انستیتوی فناوری روچستر این معما را در پیاده رو جلوی مرکز ژن ژن Polisseni ، یک عرصه هاکی روی یخ که در سال 2014 افتتاح شده است ، درج کرده است . [9]

مقایسه نمودارهای هفت پل کونیگسببرگ (بالا) و معماهای پنج اتاق (پایین). اعداد تعداد لبه های متصل به هر گره را مشخص می کنند. گره هایی با لبه های عجیب و غریب به رنگ نارنجی سایه دار هستند.

ابزارک تصویر

روز تولد

مسئلهٔ روز تولد بیان می‌کند برای یک مجموعهٔ n نفری از افراد انتخاب شده به‌طور تصادفی احتمال وجود افراد با روز تولد یکسان چقدر است؟ با استفاده از اصل لانه کبوتری می‌توان نشان داد اگر ۳۶۷ نفر را در یک اتاق جمع کنیم حداقل ۲ نفر وجود دارند که روز تولد یکسان دارند.

شمارش مو

می‌توانیم نشان بدهیم در لندن حداقل ۲ نفر وجود دارند که تعداد موی یکسانی بر سر خود دارند. از آنجا که یک فرد معمولی به‌طور متوسط ۱۵۰۰۰۰ مو بر روی سر خود دارد منطقی است که فردی با بیش از ۱۰۰۰۰۰۰ تار مو بر سر خود وجود نداشته باشد. در لندن بیش از یک میلیون نفر زندگی می‌کند اکنون تعداد لانه‌ها را برابر یک میلیون در نظر گرفته و کبوترها را تعداد افرادی که در لندن زندگی می‌کنند در نظر می‌گیریم(n>1000000) پس طبق اصل لانه کبوتری حداقل ۲ نفر وجود دارن که تعداد موی یکسانی بر روی سر خود دارند.

دست دادن

فرض کنیم n نفر وجود دارند (n>1) که هر کدام می‌توانند با دیگری دست بدهند. اصل لانهٔ کبوتری نشان می‌دهد که همیشه ۲ نفر وجود دارند که با تعداد یکسانی از افراد دست داده‌اند. هرکس می‌تواند با ۰ تا n-1 شخص دیگر دست بدهد اما تعداد لانه‌ها را n-1 در نظر می‌گیریم زیرا اگر شخصی با ۰ نفر دست دهد شخص دیگری نمی‌تواند با n-1 نفر دست بدهد و بلعکس. اکنون n-1 لانه داریم و طبق اصل لانه کبوتری حد اقل ۲ شخص (کبوتر که تعداد آنها n است) وجود دارند که با تعداد یکسان دیگری دست داده‌اند .

انتخاب جوراب

فرض کنید n جوراب آبی و m جوراب مشکی دارید(m). حداقل تعداد جوراب‌هایی که لازم است تا مطمئن شویم که یک جفت غیر همرنگ داریم برابر m+1 است. (زیرا ممکن است از بین m جوراب همگی هم‌رنگ باشند)