به سوالات زیر پاسخ دهید(سوالات ترکیب)

۱۴۰۱/۱۲/۰۱ - - علی رضا نقش نیلچی -

به چند ترییب بازیکنان می توانند در یک ردیف کنار هم بایستند
اگر باریکنان 5 و 11و21 در مکان خود ثابت بایستند بقیه بازیکنان را به چند صورت می توان کنار هم چید

مسئله های کار

۱۴۰۰/۰۹/۲۱ - - علی رضا نقش نیلچی -

جبر: مسائل کار

در این درس ها یاد خواهیم گرفت

چگونه می توان مسئله های کاری را که شامل دو نفر است حل کرد.
نحوه حل مسئله های کاری که بیش از دو نفر را درگیر می کند.
نحوه حل مسئله های کاری که شامل پر کردن مخزن توسط لوله ها می شود.

صفحه های مرتبط
ریاضی مسئله های کار
حل کار مسئله های با استفاده از جبر
بیشتر جبر درس

مسئله های کاری کاربردهای مستقیمی در زندگی واقعی دارند. ما اغلب باید تعیین کنیم که برای تکمیل یک کار در یک زمان معین به چند نفر نیاز داریم. از طرف دیگر، با توجه به تعداد محدودی از کارگران، ما اغلب باید تعیین کنیم که چقدر طول می کشد تا یک پروژه به پایان برسد. در اینجا ما با مفاهیم اساسی ریاضی در مورد نحوه رسیدگی به این نوع مسائل سروکار داریم.

چگونه مسئله های را برای دو نفر حل کنیم؟

فرمول «کار» مسائلی که دو نفر را درگیر می‌کند ، است

این فرمول برای بیش از دو نفر قابل تمدید است . همچنین می توان از آن در مسئله هایی استفاده کرد که شامل پر کردن مخزن توسط لوله ها می شود .

مثال 1:
پیتر می تواند چمن را در 40 دقیقه کنده و جان می تواند چمن را در 60 دقیقه کند. چقدر طول می کشد تا آنها چمن را با هم بچینند؟

راه حل:
مرحله 1: تعیین متغیرها :
اجازه دهید x = زمان چمن زنی با هم.

مرحله 2: از فرمول استفاده کنید:

مرحله 3: حل معادله LCM 40 و 60 120 ضرب هر دو طرف با 120

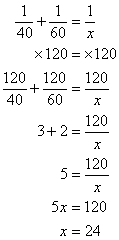
پاسخ: مدت زمانی که هر دوی آنها با هم چمن زنی می کنند 24 دقیقه است.

مثال 2:
چیدن چهل بوشل سیب ماریا 10 ساعت طول می کشد. Kayla می تواند همان مقدار را در 12 ساعت انتخاب کند. اگر با هم کار کنند چقدر طول می کشد؟ پاسخ خود را به نزدیکترین صدم گرد کنید.

مسئله های "کار": بیش از دو نفر

مثال 1:
جین، پل و پیتر می توانند نقاشی حصار را در 2 ساعت تمام کنند. اگر جین کار را به تنهایی انجام دهد، می تواند آن را در 5 ساعت تمام کند. اگر پل کار را به تنهایی انجام دهد، می تواند آن را در 6 ساعت تمام کند. چقدر طول می کشد تا پیتر به تنهایی کار را تمام کند؟

راه حل:
مرحله 1: تعیین متغیرها :
اجازه دهید x = زمان صرف شده توسط پیتر

مرحله 2: از فرمول استفاده کنید:

مرحله 3: حل معادله
هر دو طرف را در 30 x ضرب کنید

پاسخ: زمان صرف شده برای پیتر برای رنگ آمیزی حصار به تنهایی چند ساعت است.

مثال 2:
جیم می تواند در عرض 12 ساعت به تنهایی چاله ای حفر کند. جان می تواند این کار را در 8 ساعت انجام دهد و جک می تواند آن را در 6 ساعت انجام دهد. اگر با هم کار کنند چقدر طول می کشد؟

مسئله های "کار": لوله ها یک مخزن را پر می کنند

مثال 1:
یک مخزن را می توان با لوله A در 3 ساعت و توسط لوله B در 5 ساعت پر کرد. هنگامی که مخزن پر شد، می توان آن را توسط لوله C در 4 ساعت تخلیه کرد. اگر مخزن ابتدا خالی باشد و هر سه لوله باز باشد، چند ساعت طول می کشد تا باک پر شود؟

راه حل:
مرحله 1: اختصاص متغیرهای :
اجازه دهید X = زمان گرفته شده را پر کنید تا مخزن

مرحله 2: از فرمول استفاده کنید:
از آنجایی که لوله C آب را تخلیه می کند، کم می شود.

مرحله 3: معادله را حل کنید

LCM از 3، 4 و 5 60 است

هر دو طرف را در 60 ضرب کنید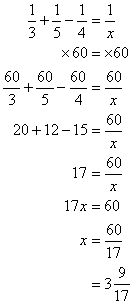

پاسخ: مدت زمان پر کردن مخزن ساعت است.

مثال 2:
لوله 1 5 روز طول می کشد تا استخر را تخلیه کند و لوله 2 7 روز طول می کشد تا استخر را تخلیه کند. چقدر طول می کشد تا این دو لوله با هم آب استخر را تخلیه کنند؟

مسئله های کار

وقتی دو نفر در حال انجام یک کار با هم با حل سیستم معادلات هستند، می توان مسائل ای را حل کرد. برای حل یک مشکل کاری، نرخ ساعتی کار دو نفر با هم را در زمان صرف شده برای کار ضرب کنید تا کل زمان صرف شده برای کار را بدست آورید. دانش حل سیستم معادلات برای حل این نوع مسائل ضروری است.

مثال:
لاتیشا و ریکی برای یک شرکت نرم افزار کامپیوتری کار می کنند. آنها با هم می توانند یک برنامه کامپیوتری خاص را در 19 ساعت بنویسند. لاتیشا می تواند در 32 ساعت برنامه را خودش بنویسد. چه مدت طول می کشد تا ریکی برنامه را به تنهایی بنویسد؟

مثال:
یک استخر شنا از طریق زهکشی در پایین استخر تخلیه می شود و توسط شیلنگ در بالا پر می شود. اگر شیلنگ بتواند استخر را در 21 ساعت پر کند و زهکشی ظرف 24 ساعت استخر را خالی کند، اگر در باز بماند چند ساعت طول می کشد تا استخر را پر کند؟ پاسخ را بر حسب ساعت بیان کنید و در صورت نیاز پاسخ را به نزدیکترین ساعت گرد کنید.

مثال :یک معادله با 4 مجهول

۱۴۰۰/۰۸/۳۰ - - علی رضا نقش نیلچی -

[1-H][M+5]+75i+7k=4

:این یک معادله با 4 مجهولی است و مجهولات عبارتند از

H,M,i,k

در این معادله درجه آزادی 3 است

یعنی با دادن سه مقدار به سه مجهول می توان یک مجهول دیگر را بدست آورد

مثال :متغیر و پارامتر در یک تابع

۱۴۰۰/۰۸/۳۰ - - علی رضا نقش نیلچی -

f(x)=[x-3]/n

در این مثال n پارامتر تابع و x متغیر تابع است

مثال از محاسبه معکوس تابع

۱۴۰۰/۰۸/۳۰ - - علی رضا نقش نیلچی -

F(X)=6X+7

6X+7=Y

6x=y-7

X=(y_7)/6

F^-1(X)=(x-7)/6

مثال از جایگشت با تکرار:تعداد جایگشت های appearing

۱۳۹۹/۰۴/۰۷ - - علی رضا نقش نیلچی -

محاسبه جایگشت

۱۳۹۹/۰۲/۱۹ - - علی رضا نقش نیلچی -

فرض کنید می‌خواهیم $n$ دانش آموز (به عنوان اشیا متمایز) را در یک صف قرار دهیم:

در جایگاه اول ممکن است هر یک از $n$ دانش آموز بایستند پس برای مکان اول (ابتدای صف) $n$ حالت مختلف وجود دارد. در جایگاه دوم $n-1$ دانش آموز باقی‌مانده (به جز دانش آموزی که در جایگاه اول صف ایستاده) می‌توانند قرار بگیرند پس تا اینجا به $n\times (n-1)$ حالت مختلف توانستیم دو مکان اول را با دو دانش‌آموز پر کنیم. به همین ترتیب برای جایگاه سوم:

$n\times (n-1)\times (n-2)$

حالت و برای $i$ امین جایگاه به تعداد:

$n\times (n-1)\times (n-2)\times \dots \times (n-i+1)$

حالت داریم. با همین روند تمام $n$ جایگاه را به:

$n\times (n-1)\times (n-2)\times \dots \times 2\times 1$

طریق می‌توان با $n$ دانش آموز پر کرد؛ که همان تعداد روش‌های ایستادن $n$ دانش آموز در یک صف می‌باشد. حاصل ضرب فوق را «جایگشت $n$ شی متمایز» می‌نامند و آن را با نماد $n!$ (خوانده می‌شود $n$ فاکتوریل) نشان می‌دهند.

تعریف جایگشت (خطی)

۱۳۹۹/۰۲/۱۹ - - علی رضا نقش نیلچی -

تعریف

جایگشت (خطی): هر ترتیب dfsd (خطی) قرار گرفتن n شی در کنار هم را یک جایگشت می‌نامند. در مسایل ترکیبیاتی اکثراً تعداد جایگشت‌ها مد نظر است.

تابع گویا

۱۳۹۹/۰۱/۳۱ - - علی رضا نقش نیلچی -

تابع گویا

در ریاضیات، تابع گویا به تابعی گفته می‌شود که آن را به صورت تابع چندجمله‌ای می‌توان نوشت. الزامی ندارد که ضرایب چندجمله‌ یا حتی مقادیری که تابعی به عنوان ورودی می‌گیرد، حتماً اعدادی گویا باشد.

تعاریف

تابع تک متغیرهٔ $f\,$ گویاست اگر و فقط اگر بتوان آن را به شکل زیر نوشت:

$f(x)={\frac {P(x)}{Q(x)}}$

که در آن، $P\,$ و $Q\,$ توابعی چندجمله‌ای از $x\,$ هستند و $Q\,$ چندجمله‌ای صفر نیست. دامنهٔ $f\,$ مجموعهٔ همهٔ نقاطی است که به اِزای آن‌ها مخرجِ $Q(x)\,$ مخالفِ صفر است.

تمامی توابع چندجمله‌ای توابعی گویا با $Q(x)=1$ هستند. توابعی که نمی‌توان آن‌ها را بدین شکل نمایش داد؛ مثلاً $f(x)=\sin(x)$ گویا نیستند.

عبارتی که به شکل ${\frac {P(x)}{Q(x)}}$ است، عبارت گویا نامیده می‌شود. نیازی نیست که $x$ متغیر باشد.

معادلهٔ گویا به معادله‌ای گفته می‌شود که دو عبارت گویا با هم برابر قرار داده شده‌اند. این عبارات از همان قواعد حاکم بر کسرها تبعیت می‌کنند. این‌گونه معادلات را با روش دور در دور، نزدیک در نزدیک می‌توان حل کرد. از آن‌جایی که تقسیم بر صفر تعریف نشده‌است، لذا جواب‌هایی که باعث تقسیم بر صفر می‌شود، قابل قبول نیست.

دامنه

یادمان باشد ریشه‌های مخرج تعریف نمی‌شوند.

فرم کلی دامنه تابع گویا به صورت زیر است:

$D=\mathbb {R} -\{Q=0\}$

خلاصه تابع گویا

تعریف تابع گویا و دامنه آن

توابع زوج و فرد

۱۳۹۹/۰۱/۳۱ - - علی رضا نقش نیلچی -

توابع زوج و فرد

در ریاضیات، توابع زوج و توابع فرد، توابعی هستند که در مورد بعضی روابط قرینگی، در رابطه با وارون‌های افزایشی به بحث می‌پردازد. این توابع در بسیاری از زمینه‌های آنالیز ریاضی کاربرد دارند،

توابع زوج

$f(x)=x^{2}$ ، مثالی از یک تابع زوج

فرض می‌کنیم ‎f(x)‎ تابعی حقیقی باشد. آن‌گاه f، زوج است اگر رابطهٔ زیر برای تمام xهای در دامنهٔ f برقرار باشد:

$f(x)=f(-x).$ ‎

به طور هندسی، یک تابع زوج، نسبت به محور yها قرینه است، که معنی آن این است که با بازتاباندن هر قسمتی از تابع نسبت به محور yها، تابع بدون تغییر بماند.

مثال‌هایی از توابع زوج، تابع ثایت ‎f(x) = c‎، ‎cos(x)‎، و ‎cosh(x)‎ می‌باشند.

توابع فرد

$f(x)=x^{3},$ مثالی از یک تابع فرد

فرض می‌کنیم ‎f(x)‎ تابعی حقیقی باشد. آن‌گاه f، فرد است اگر رابطهٔ زیر برای تمام xهای در دامنهٔ f برقرار باشد:

$-f(x)=f(-x).$ ‎

به طور هندسی، یک تابع فرد، نسبت به مبدأ مختصات تقارن دارد، که معنی آن این است که تابع بعد از چرخشی ۱۸۰ درجه‌ای، بدون تغییر می‌ماند. در واقع مبدا مختصات نقطه عطف این نوع تابع ها می باشد.

مثال‌هایی از تابع فرد، تابع همانی ‎ f(x) = x‎، ‎x3‎، ‎sin(x)‎ و ‎sinh(x)‎ می‌باشند.

خواص پایه[ویرایش]

تنها تابعی که هم زوج و هم فرد است، تابع ثابت صفر است. (برای مثال برای هر x داریم: f(x) = ۰)
مجموع یک تابع زوج و یک تابع فرد، نه زوج است نه فرد، مگر یکی از آن‌ها عیناً صفر باشد.
مجموع دو تابع زوج، تابعی زوج است، و حاصلضرب هر عدد ثابت در یک تابع زوج، زوج است.
مجموع دو تابع فرد، تابعی فرد است، و حاصلضرب هر عدد ثابت در یک تابع فرد، فرد است.
حاصل‌ضرب دو تابع زوج، تابعی زوج است.
حاصل‌ضرب دو تابع فرد، تابعی زوج است.
حاصل‌ضرب یک تابع زوج و یک تابع فرد، تابعی فرد است.
حاصل تقسیم دو تابع زوج، تابعی زوج است.
حاصل تقسیم دو تابع فرد، تابعی زوج است.
حاصل تقسیم یک تابع زوج و یک تابع فرد، تابعی فرد است.
مشتق یک تابع زوج، تابعی فرد است.
مشتق یک تابع فرد، تابعی زوج است.
ترکیب دو تابع زوج، تابعی زوج است، و ترکیب دو تابع فرد، تابعی فرد است.
ترکیب یک تابع زوج و یک تابع فرد، تابعی زوج است.
ترکیب هر تعداد تابعی که در میان آن‌ها تنها یک تابع زوج وجود داشته باشد، تابعی زوج است (اما نه به عکس).
انتگرال یک تابع فرد از A- تا A+، صفر است (در صورتی که A کران‌دار باشد، و تابع در فاصلهٔ A- تا A+، هیچ مجانب قائمی نداشته باشد).
انتگرال یک تابع زوج از A- تا A+، دوبرابر انتگرال از ۰ تا A+ است (در صورتی که A کران‌دار باشد، و تابع در فاصلهٔ A- تا A+، هیچ مجانب قائمی نداشته باشد)

معادله خط

۱۳۹۹/۰۱/۳۱ - - علی رضا نقش نیلچی -

$\ displaystyle y = mx + b$

جایی که: X است متغیر مستقل از تابع( Y = F ( X .

شیب خط از طریق نقاط ${\ نمایشگر A (x_ {a} ، y_ {a})}$ و ${\ نمایشگر B (x_ {b} ، y_ {b})}$ ، زمانی که $\ displaystyle x_ {a} \ neq x_ {b}}$ ، از رابطه زیر بدست می آید $\ displaystyle m = (y_ {b} -y_ {a}) / (x_ {b} -x_ {a})$ و معادله این خط را می توان نوشت ${\ displaystyle y = m (x-x_ {a}) + y_ {a}$ .

تعریف تابع

۱۳۹۹/۰۱/۳۱ - - علی رضا نقش نیلچی -

تابع را می‌توان به عنوان قاعده‌ای خاص برای تناظر بین اعضای دو مجموعهٔ دامنه و برد تعریف کرد. به بیان دقیق‌تر، اگر $A$ و $B$ دو مجموعه باشند، یک تابع از مجموعهٔ $A$ به مجموعهٔ $B$ را می‌توان قاعده‌ای تعریف کرد که به هر عضو مجموعهٔ $A$ مانند $a$ ، یک و فقط یک عضو از مجموعهٔ $B$ را مانند $f(a)$ نسبت می‌دهد. تابع $f$ از مجموعهٔ $A$ به مجموعهٔ $B$ را با $f:A\to B$ نشان می‌دهیم.

شکل ۱. نمونه‌ای از یک تناظر که تابع نیست.

شکل ۲. نمونه‌ای از یک تابع

برای نمونه تناظر شکل ۱ نمایش‌دهندهٔ یک تابع نمی‌باشد. چراکه عضو ۳ از مجموعه $X$ به دو عضو ( $b$ و $c$ ) از $Y$ متناظر شده‌است. اما شکل ۲ نشان دهنده یک تابع است. هر چند که دو عضو گوناگون از مجموعه { $X$ به یک عضو خاص از $Y$ نسبت داده شده‌اند.

تابع $f$ به عنوان هنجار تناظر، چیزی بجز توصیف نحوهٔ تناظر اعضای $A$ به $B$ نیست که به‌طور کامل به‌وسیله همه زوج‌های مرتب $(a,f(a))$ برای هر $a\in A$ مشخص می‌شود. پس تابع $f$ را می‌توان به عنوان مجموعه‌ی همه این زوج‌های مرتب، یعنی مجموعهٔ همه زوج‌های مرتبی که مؤلفه اول آن‌ها عضو $A$ بوده و مؤلفه دوم آن‌ها تصویر مؤلفه اول تحت تابع $f$ در $Y$ است، تعریف کرد. شرط تابع بودن تضمین می‌کند که هیچ دو زوج متمایزی در تابع $f$ دارای مؤلفهٔ اول یکسان نخواهند بود.

در این صورت در تابع $f:A\to B$ برای هر $a\in A$ گزارهٔ $(a,b)\in f$ را به صورت $b=f(a)$ نشان می‌دهیم.

تعریف دقیق[ویرایش]

یک تابع از مجموعه $X$ به مجموعه $Y$ ، رابطه‌ای چون $f$ از مجموعه $X$ به مجموعه $Y$ است که دارای شرایط زیر باشد:

دامنه $f$ مجموعه $X$ باشد، یعنی $domf=X$ .
برای هر $x\in X$ عنصر یگانه $y\in Y$ موجود باشد که $(x,y)inf$ یا به عبارتی هیچ دو زوج مرتب متمایزی متعلق به $f$ دارای مؤلفه اول یکسان نباشند. شرط یگانگی را به‌طور صریح می‌توان یه این صورت فرمول بندی کرد که اگر $(x,y)\in f$ و $(x,z)\in f$ آنگاه الزاماً $y=z$ .

تابع

۱۳۹۹/۰۱/۳۱ - - علی رضا نقش نیلچی -

نمودار متحرک رسم تغییرات توابع: ${\sqrt[{n}]{x}}=y$ با دامنه: $n=\{2,3,...,31\}$
$x=\{0...+1\}$
$y=\{0...+1\}$
توابع ریشه nام x را نشان می‌دهند.
عدد متغیر در تصویر معادل n می‌باشد.

به‌طور ساده می‌توان گفت که به قاعده‌های تناظری که به هر ورودی خود یک و فقط یک خروجی نسبت می‌دهند، تابع گفته می‌شود.

نمودارتغییرات سکه امامی (طرح جدید) را رسم کنید

۱۳۹۷/۱۰/۲۷ - - علی رضا نقش نیلچی -

سکه امامی (طرح جدید) روز گذشته را با نرخ 3 میلیون و 890 هزار تومان به پایان رساند و امروز با نرخ 3 میلیون و 885 هزار تومان بازگشایی شد. در معاملات اولیه سکه تا 3 میلیون و 873 هزار تومان نیز کاهش یافت اما با نزدیک شدن به ظهر به مرز 3.9 میلیونی نزدیک شد و پس از ظهر وارد کانال 3.9 میلیونی شد. در ادامه قیمت سکه طرح جدید تا میانه این کانال پیشروی کرد و در لحظه تنظیم گزارش (حوالی ساعت 4 بعدازظهر) سکه در بازار تهران 3 میلیون و 940 هزار تومان معامله می‌شود.

نمودارتغییرات سکه امامی (طرح جدید) رابرای امروز رسم کنید

معادلات درجه 2

۱۳۹۷/۱۰/۰۵ - - علی رضا نقش نیلچی -

در معادله های زیر دلتا را بدست آورید:
13x²-15x-29=0
2x²-50=0
معادله را حل کنید

3x²-x=0
معادله را حل کنید

3x²-5x+2=0

معادله درجه 2

۱۳۹۷/۰۹/۲۴ - - علی رضا نقش نیلچی -

دل نوشته ها ی نقش و آموزش ریاضی

نوشته هائی در باره بازگشت به خود و مسائل ریاضی و آموزش آن

به سوالات زیر پاسخ دهید(سوالات ترکیب)

مسئله های کار

جبر: مسائل کار

چگونه مسئله های را برای دو نفر حل کنیم؟

مسئله های "کار": بیش از دو نفر

مسئله های "کار": لوله ها یک مخزن را پر می کنند

مسئله های کار

مثال :یک معادله با 4 مجهول

مثال :متغیر و پارامتر در یک تابع

مثال از محاسبه معکوس تابع

F^-1(X)=(x-7)/6

مثال از جایگشت با تکرار:تعداد جایگشت های appearing

محاسبه جایگشت

تعریف جایگشت (خطی)

تعریف

تابع گویا

تابع گویا

تعاریف

دامنه

خلاصه تابع گویا

توابع زوج و فرد

توابع زوج و فرد

توابع زوج

توابع فرد

خواص پایه[ویرایش]

معادله خط

تعریف تابع

تابع

نمودارتغییرات سکه امامی (طرح جدید) را رسم کنید

معادلات درجه 2

معادله درجه 2

مشخصات وب

موضوعات وب

پیوندها

آرشیو وب

آمارگیر وبلاگ

آمارگیر وبلاگ

کد پربازدیدترین