​

جداسازی مجموعه ها با استفاده از نمودار ون

جداسازی مجموعه ها با استفاده از نمودار ون توسط دو ناحیه بسته غیر همپوشانی نشان داده می شود و اجزای گفته شده با نشان دادن یک منحنی بسته که به طور کامل در داخل دیگری قرار دارد نشان داده می شوند.

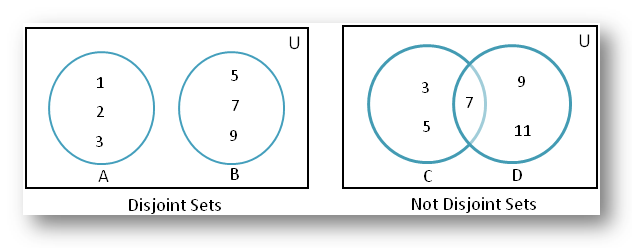
دو مجموعه A و B در صورتی که هیچ عنصر مشترکی نداشته باشند جدا هستند.

بنابراین، A = {1، 2، 3} و B = {5، 7، 9} مجموعه‌های جدا هستند. اما مجموعه های C = {3، 5، 7} و D = {7، 9، 11} جدا نیستند. برای، 7 عنصر مشترک A و B است.

اگر A ∩ B = ϕ به دو مجموعه A و B جدا گفته می شود. اگر A ∩ B ≠ ϕ، A و B مجموعه هایی متقاطع یا همپوشانی هستند.

نمونه هایی برای نشان دادن جدایی مجموعه ها با استفاده از نمودار ون:

1.

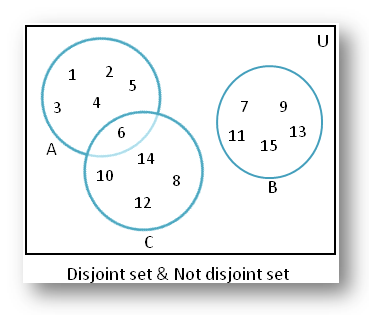
اگر A = {1، 2، 3، 4، 5، 6}، B = {7، 9، 11، 13، 15} و C = {6، 8، 10، 12، 14}، A و B جدا نیستند. مجموعه ها از آنجایی که هیچ عنصر مشترکی ندارند در حالی که A و C مجموعه های متقاطع هستند زیرا 6 عنصر مشترک در هر دو است.

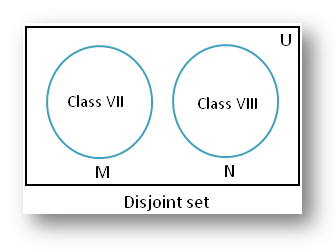
2. (i) اجازه دهید M = مجموعه ای از دانش آموزان کلاس VII

و N = مجموعه ای از دانش آموزان کلاس هشتم

از آنجایی که هیچ دانش آموزی نمی تواند در هر دو کلاس مشترک باشد. بنابراین مجموعه M و مجموعه N جدا هستند.

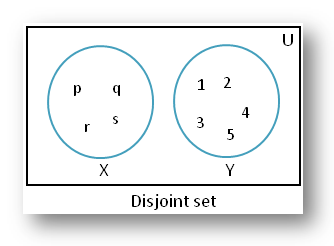
(ii)  X = {p، q، r، s} و Y = {1، 2، 3، 4، 5}

واضح است که مجموعه X و مجموعه Y هیچ عنصر مشترکی برای هر دو ندارند. بنابراین مجموعه X و مجموعه Y مجموعه‌های جدا هستند.

3.

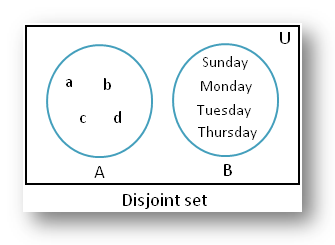
A = {a، b، c، d} و B = {یکشنبه، دوشنبه، سه شنبه، پنج شنبه} از هم جدا هستند زیرا هیچ عنصر مشترکی ندارند.

4.

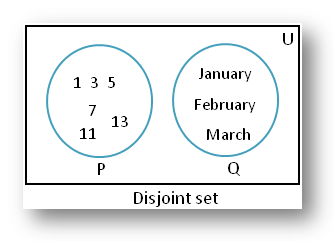
P = {1، 3، 5، 7، 11، 13} و Q = {ژانویه، فوریه، مارس} از هم جداسازی ه هستند زیرا هیچ عنصر مشترکی ندارند.

توجه داشته باشید:

1. محل تلاقی دو مجموعه مجزا همیشه مجموعه خالی است.

2. در هر نمودار ون ∪ مجموعه جهانی و A، B و C زیر مجموعه های ∪ هستند.

​