جزییات از نمودار ون برای استفاده از احتمالات چند رویداد مفید است. در شماره 1 زیر استفاده از بررسی و تعیین احتمالات رویدادهای فردی، رویدادها و تعریف یک رویداد را می کنیم. در شماره 3 به بررسی احتمال شرطی و نحوه استفاده از نمودار ون برای حل این مسائل و همچنین فرمول شرطی تصمیم پرداخت.
بیایید از نمودار ون زیر برای یافتن احتمالات زیر استفاده کنیم.
توجه داشته باشید که مجموع تمام اسناد در نمودار است 0.4+0.3+0.2+0.1=1. این تصویر کل فضای نمونه را برای دو رویداد نشان می دهد،A و B.
- P(A)
برای پیدا کردن P(A)، ما فقط احتمال آن را اضافه می کنیم A به این احتمال رخ می دهد که A و B رخ می دهد برای گرفتن 0.4+0.3=0.7. بنابراینP(A)=0.7.
- P(B)
به همین ترتیب، P(B)=0.2+0.3=0.5.
- P(A∩B)
اکنون، P(A∩B) مقدار در ناحیه همپوشانی 0.3 است.
P(A∪B)
P(A∪B)=0.4+0.3+0.2=0.9. که با استفاده از فرمول نیز قابل یافتن استP(A)+P(B)−P(A∩B)=0.7+0.5−0.3=0.9.
P(A′∩B′)
P(A′∩B′) با یافتن خارج از محل که در باید همه چیز از آن مشخص شود A با همه چیز خارج از آن همپوشانی دارد B. این منطقه خارج از هر دویره خواهد بود و احتمال آن 0.1 است. راه دیگری برای فکر کردن به این استP(A∪B)′، یا 1−P(A∪B).
قانون دی مورگان
چند نماد مجموعه معادل در مورد احتمالات وجود دارد و آنها را قوانین دی مورگان می نامند.
(A∩B)′=(A′∪B′) برای مجموعه یا P(A∩B)′=P(A′∪B′) برای احتمالات
و
(A∪B)′=(A′∩B′) برای مجموعه یا P(A∪B)′=P(A′∩B′) برای احتمالات
حال بیایید مشکلات زیر را حل کنیم.
- داده شده است P(A)=0.6، P(B)=0.3 و P(A∪B)=0.7، پیدا کردن P(A∩B) و P(A′∪B′).
ابتدا مجموعه ای از فرمول اتحاد دو برای تعیین تقاطع استفاده کنیم.
P(A)+P(B)−P(A∩B)0.6+0.3−P(A∩B)0.9−0.70.2=P(A∪B)=0.7=P(A∩B)=P(A∩B)
اکنون می از قانون دی مورگان برای پیدا کردن استفاده کنیم P(A′∪B′).
P(A′∪B′)=P(A∩B)′=1−P(A∪B)=1−0.2=0.8.
ما همچنین می توانیم یک نقشه را برای احتمالات ایجاد کنیم و تفسیر کنیم P(A′∪B′) و مناطق خارج از کشور A اتحاد با مناطق خارج B که همه چیز در نظر خواهد بود به همپوشانی دو منطقه یا P(A∩B).
- دادههای یک نظرسنجی از 140 دانشآموز نشان داد که 37 نفر موسیقی مطالعه میکنند، 103 نفر ورزش میکنند و 25 نفر هیچ کدام را انجام نمیدهند. یک نمودار ون ایجاد کنید تا داده های جمع آوری شده را نشان دهد و سپس این احتمال را تعیین کنید که اگر دانش آموزی به طور تصادفی انتخاب شود،
- او موسیقی خواهد خواند
- او با توجه به اینکه یک ورزش انجام می دهد، موسیقی را مطالعه می کند.
اجازه دهید M نشان دهنده مجموعه دانش آموزانی است که موسیقی می خوانند و Sنشان دهنده مجموعه دانش آموزانی است که ورزش می کنند. ابتدا تعداد دانشآموزانی که موسیقی مطالعه میکنند و ورزش میکنند را مشخص میکنیم تا ناحیه همپوشانی در نمودار را پر کنیم و سپس میتوانیم مقادیر دیگر را پیدا کنیم.
n(M)+n(S)−n(M∩S)37+103−n(M∩S)n(M∩S)=n(M∪S)=115=25
- احتمال اینکه یک دانش آموز به طور تصادفی انتخاب شده موسیقی را مطالعه کند، تعداد دانش آموزانی است که موسیقی مطالعه می کنند تقسیم بر تعداد کل دانش آموزان مورد بررسی یا P(M)=n(M)140=37140≈0.264.
- احتمال اینکه دانش آموزی که به طور تصادفی انتخاب می شود با توجه به اینکه یک ورزش را انجام می دهد، موسیقی مطالعه کند، احتمال شرطی نامیده می شود. ما از علامت گذاری استفاده می کنیمP(M|S) به نمایندگی از P(M) با توجه به اینکه Sقبلا رخ داده است. برای یافتن این احتمال با استفاده از نمودار ون، تعداد دانشآموزانی که موسیقی مطالعه میکنند و یک ورزش را انجام میدهند را پیدا میکنیم و بر تعداد دانشآموزانی که ورزش میکنند یا تقسیم میکنیم.P(M|S)=n(M∩S)n(S)=25103≈0.243. این طور فکر کنید، وقتی می گوییم می دانیم که دانش آموز یک ورزش را انجام می دهد، پس شمارش به دانش آموزانی محدود می شود که موسیقی می خوانند و یک ورزش انجام می دهند و مخرج محدود به کسانی است که ورزش می کنند.
همچنین یک فرمول برای احتمال شرطی وجود دارد: P(A|B)=P(A∩B)P(B)
در زمینه مشکل ما این است: P(M|S)=P(M∩S)P(S)=25140103140=25140⋅140103=25103.
توجه داشته باشید که احتمال به دست آمده همان است که قبلا تعیین شده است. از هر دو روش می توان استفاده کرد.
مثال ها
مثال 1
پیش از این، از شما خواسته شد که این احتمال را پیدا کنید که یکی از آن مشتریانی که به طور تصادفی انتخاب شده اند، آب نبات پنبه دندی را بخواهند.
نمودار ون برای این وضعیت 12 را نشان می دهد، تعداد مشتریانی که هر دو طعم را دوست دارند، به عنوان تقاطع. بنابراین تعداد مشتریانی که فقط طعم Pumpernickel را دوست دارند، خواهد بود32−12=20 در حالی که تعداد مشتریانی که فقط طعم آب نبات پنبه را دوست دارند، خواهد بود 58−12=46. از آنجایی که 21 مشتری وجود دارد که هیچ طعمی را دوست ندارند، تعداد کل مشتریان مورد نظرسنجی است12+20+46+22=100 و این احتمال وجود دارد که یکی از آن مشتریانی که به طور تصادفی انتخاب شده است طعم آب نبات پنبه را بپسندد 58100=58%.
مثال 2
در کلاسی متشکل از 260 نفر از سالمندان، 93 نفر اسپانیایی، 95 نفر شیمی، 165 نفر ریاضی، 18 نفر اسپانیایی و شیمی، 75 نفر شیمی و ریاضی، 20 نفر ریاضی و اسپانیایی و 15 نفر در هر سه موضوع مطالعه میکنند. یک نمودار ون برای نشان دادن داده ها بسازید و سپس احتمال انتخاب دانش آموز در مطالعات تصادفی را بیابید:
فقط اسپانیایی
P(S∩M′∩C′)=70260=726≈0.269
ریاضی و شیمی اما اسپانیایی نه
P(M∩C∩S′)=60260=313≈0.231
هیچ کدام از این موضوعات
P(M′∩C′∩S′)=5260=152≈0.0192
اسپانیایی، با توجه به اینکه او ریاضی می خواند
P(S|M)=P(S∩M)P(M)=20260165260=433≈0.121
مثال 3
داده شده P(A∩B)=0.4، P(A∩B′)=0.2 و P(A′∩B′)=0.3، پیدا کردن P(B) و P(A|B).
اطلاعات نمودار ون را به ما می دهد:
مقدار گمشده، P(B∩A′)، باید 0.1 باشد تا مجموع احتمالات موجود در فضای نمونه برابر 1. بنابراین، P(B)=0.5. P(A|B)=P(A∩B)P(B)=0.40.5=45=0.8.
مرور
برای سؤالات 1-3، احتمالات نشان داده شده را پیدا کنید P(A)=0.5، P(B)=0.65 و P(A∪B)=0.75.
- P(A∩B)
- P(A′∩B′)
- P(B|A)
برای سؤالات 4-6، احتمالات داده شده را پیدا کنید P(A)=0.6، P(B)=0.8 و P(A∪B)′=0.2.
- P(A∩B′)
- P(B|A)
- P(A|B)
برای سؤالات 7-9، احتمالات داده شده را پیدا کنید P(A∩B′)=0.3، P(B∩A′)=0.2 و P(A∪B)=0.8.
- P(A∩B)
- P(A)
- P(B|A)
- داده شده P(A)=2P(B)، P(A∪B)=0.8 و P(A∩B)=0.1، پیدا کردن P(A).
- باشگاه بین المللی در یک مدرسه دارای 105 عضو است که بسیاری از آنها به چندین زبان صحبت می کنند. رایج ترین زبان های این باشگاه انگلیسی، اسپانیایی و چینی است. از نمودار ون زیر برای تعیین احتمال انتخاب دانش آموزی استفاده کنید که:
- انگلیسی صحبت نمی کند
- با توجه به اینکه انگلیسی صحبت می کند اسپانیایی صحبت می کند.
- با توجه به اینکه چینی صحبت می کند انگلیسی صحبت می کند.
- اسپانیایی و انگلیسی صحبت می کند اما چینی را نه.

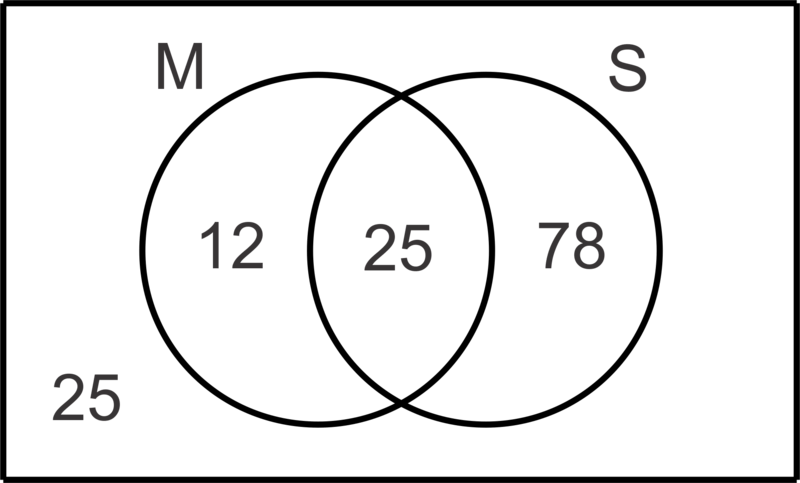



 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.