f(x)=xsinx+cosx−tanx at x=−1?

قانون سینوس ها

با دایره محیطی

بدون دایره

دو مثلث با مولفه های قانون سینوس ها. α ، β و γ به ترتیب زوایای مرتبط با رئوس با بزرگ A ، B و C هستند. حروف کوچک a ، b و c طول اضلاع مقابل آنها هستند. ( a مقابل α و غیره است)

که در آن a ، b ، و c طول اضلاع یک مثلث، و α ، β ، و γ زاویه مقابل هستند (شکل سمت چپ را ببینید)، در حالی که R است شعاع از مثلث دایره محیطی . وقتی از آخرین قسمت معادله استفاده نمی شود، گاهی اوقات قانون با استفاده از حرکات متقابل بیان می شود .

قانون سینوس ها را می توان برای محاسبه اضلاع باقیمانده یک مثلث زمانی که دو زاویه و یک ضلع شناخته شده است استفاده کرد - تکنیکی که به عنوان مثلث سازی شناخته می شود . همچنین زمانی می توان از آن استفاده کرد که دو ضلع و یکی از زوایای غیر محصور مشخص باشد. در برخی از این موارد، مثلث به طور منحصر به فرد توسط این داده تعیین نمی شود (به نام حالت مبهم ) و این تکنیک دو مقدار ممکن برای زاویه محصور می دهد.

قانون سینوس ها یکی از دو معادله مثلثاتی است که معمولاً برای یافتن طول و زاویه در مثلث های مقیاسی به کار می رود و دیگری قانون کسینوس ها است .

قانون سینوس ها را می توان به ابعاد بالاتر در سطوح با انحنای ثابت تعمیم داد. [1]

تاریخچه [ ویرایش ]

طبق گفته های Ubiratàn D'Ambrosio و Helaine Selin ، قانون کروی سینوس ها در قرن دهم کشف شد. به اقسام مختلف به ابومحمود خجندی ، ابوالوفاء بوزجانی ، نصیرالدین طوسی و ابونصر منصور نسبت داده شده است . [2]

بن معاذ AL-Jayyānī اون کتاب کمان ناشناخته از یک کره در قرن 11th شامل قانون کلی سینوس. [3] قانون صفحه سینوس ها بعداً در قرن سیزدهم توسط نصیرالدین طوسی بیان شد . او در «شکل بخش» قانون سینوس‌ها را برای مثلث‌های مسطح و کروی بیان کرد و برای این قانون شواهدی ارائه کرد. [4]

به گفته گلن ون بروملن ، "قانون سینوس ها در واقع پایه و اساس Regiomontanus برای حل مثلث های قائم الزاویه او در کتاب چهارم است، و این راه حل ها به نوبه خود پایه هایی برای حل مثلث های کلی او هستند." [5] Regiomontanus یک ریاضیدان آلمانی قرن پانزدهم بود.

اثبات [ ویرایش ]

مساحت T هر مثلثی را می توان نصف قاعده آن ضربدر ارتفاعش نوشت. با انتخاب یک ضلع مثلث به عنوان پایه، ارتفاع مثلث نسبت به آن قاعده بر حسب طول ضلع دیگر ضربدر سینوس زاویه بین ضلع انتخاب شده و پایه محاسبه می شود. بنابراین بسته به انتخاب پایه، مساحت مثلث را می توان به صورت یکی از موارد زیر نوشت:

ضرب اینها در 2/abc می دهد

در حل معادله مراحل زیر را  انجام داد :

1- در سطر دوم مخرج مشتر ک بدست آمده است.

2-در سطر سوم کسر در مخرج مشترک ضرب شده است

3-در سطر چهارم ضربها را انحام داد

4-در سطر پنجم عبارت را تاحد امکان ساده شد

5-در ادامه معادله بدست آمده باروش تجزیه حل شد

فرض کنید که Y = g ( X ) است تابع معکوس . تابع معکوس آن را f بنامیم تا x = f ( y ) داشته باشیم . یک فرمولی برای مشتق f بر حسب مشتق g وجود دارد . برای مشاهده این موضوع، توجه داشته باشید که f و g فرمول را برآورده می کنند

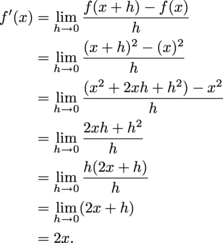
و چون توابع و x مساوی هستند، مشتقات آنها باید برابر باشند. مشتق x تابع ثابت با مقدار 1 و مشتق از استتوسط قانون زنجیره تعیین می شود. بنابراین، ما داریم که:

برای بیان f' به عنوان تابعی از متغیر مستقل y ، جایگزین می کنیمبرای x هر کجا ظاهر شود. سپس می توانیم برای f را حل کنیم .

قانون زنجیره بیان می کند که مشتق ترکیب آنها در نقطه x = a است:

این را می توان به عنوان ترکیبی از سه تابع تجزیه کرد:

مشتقات آنها عبارتند از:

f(x,y,z)=ax+by-z

در این مثالa ,b پارامتر های تابع و x  ,y,z متغیرهای تابع است

             f'(x)=-2x-6

f(x)=-x^2-6X

  F(X)=6X+7

6X+7=Y

6x=y-7

X=(y_7)/6

F^-1(X)=(x-7)/6