دل نوشته ها ی نقش و آموزش ریاضی  

هنگامی که یک تابع ضرب دو تابع است یا می تواند به عنوان چنین کالایی تجزیه شود ، آنگاه قضیه زیر به ما اجازه می دهد تا مشتق آن را بیابیم:

اگر( y = f ( x ) g ( x  ، سپس

[ f ( x ) g ( x )] '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

راه دیگر برای نوشتن این مقاله ، با استفاده از نماد Leibniz است

توجه کنید که مشتق یک محصول از توابع فقط محصول مشتقات آنها نیست؛ این مشتق تا حدودی پیچیده تر است. به این معنا که،

در عوض ، ما داریم

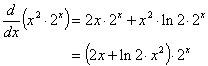
مثال ها:

1. صرب 

f ( x ) = (2 x + 1) ( x 2 - 2).

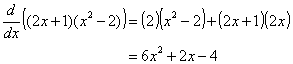
باید توجه کنید که اگر ابتدا محصول را ساده کردید ، سپس مشتق آن را بگیرید ، نتیجه همان  خواهد بود.

2. مثال دیگر:

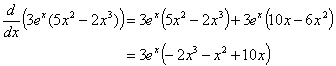
فاکتورسازی نتیجه در انتها معمولاً برای جبری یافتن نقاط بحرانی و فواصل افزایش / کاهش مناسب است.

3. نمونه ای از توابع عددی تعریف شده. بگذارید f (2) = 1، f '(2) = -1 ، g (2) = -3 و g' (2) = 4. مشتقات (f ( x ) g ( x  را در x = 2 پیدا کنید .

راه حل: طبق قانون ضرب ، مشتق ضرب f و g در x = 2 است

f '(2) g (2) + f (2) g ' (2) = (-1) (- 3) + (1) (4) = 7