مثال 1: مشتق تابع f داده شده را پیدا کنید

راه حل برای مثال 1: تابع f ضرب دو تابع است: U = x 2 - 5 و V = x 3 - 2 x + 3؛ از این رو

ما از قانون ضرب برای تمایز f به شرح زیر استفاده می کنیم:

که در آن U و V به ترتیب مشتقات U و V هستند و توسط آنها داده می شود

جایگزین برای به دست آوردن

گسترش ، گروه بندی و ساده سازی کنید

مثال 2: اولین مشتق تابع f داده شده توسط آن را محاسبه کنید

$f(x) = (\sqrt x + 2x)(4x^2-1)$

راه حل برای مثال 2: این تابع ممکن است ضرب تابع U = √x + 2x و V = 4x 2 - 1 محسوب شود ، از این رو استفاده از قانون ضرب

$f'(x) = U' V + U V' \\= (\dfrac{1}{2\sqrt x} + 2)(4x^2-1) + (\sqrt x + 2 x)(8x)$

برای افزودن موارد فوق ، باید همه اصطلاحات را به عنوان کسری با مخرج مشترک بنویسید.

$f'(x) = \dfrac{(1+2\cdot2\sqrt x)(4x^2-1)+2\sqrt x(8x)(\sqrt x + 2x)}{2\sqrt x}$

بسط دادن

$f'(x) = \dfrac{4x^2-1+16x^{5/2}-4\sqrt x+16x^2+32x^{5/2}}{2\sqrt x}$

و گروه برای به دست آوردن نتیجه نهایی برای مشتق f به شرح زیر است.

$f'(x) = \dfrac{48x^{5/2}+20x^2-4x^{1/2}-1}{2\sqrt x}$

مثال 3: اولین مشتق تابع f داده شده توسط آن را محاسبه کنید

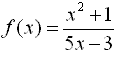
نمونه عملکرد 3 مشتق را پیدا کنید

راه حل به مثال 3:
تابع داده شده به عنوان نسبت دو تابع در نظر گرفته می شود: U = x 2 + 1 و V = 5x - 3 و با استفاده ازقاعده ی تقسیم برای تمایز f از این روش استفاده می شود.

راه حل مشتق به مثال 3 ، مرحله 1

گسترش و گروه را بدست آورید تا( f '(x را به شرح زیر بدست آورید

راه حل مشتق به مثال 3 ، مرحله 2

مثال 4: اولین مشتق تابع f داده شده توسط آن را محاسبه کنید

مثال عملکرد 4 مشتق را پیدا کنید

راه حل برای مثال 4: تابع f ، از دو تابع استفاده می کند ، از این رو استفاده از قانون تقسیم است

راه حل مشتق به مثال 4 ، مرحله 1

همه عبارات را در اعداد بنویسید به طوری که آنها دارای مخرج یکسان باشند

راه حل مشتق به مثال 4 ، مرحله 2

برای به دست آوردن f '(x) عبارات را مانند گروه گسترش داده و گروه بندی کنید

راه حل مشتق به مثال 4 ، مرحله 3

مثال 5: اولین مشتق تابع f داده شده توسط آن را محاسبه کنید

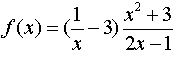
مثال عملکرد 5 مشتق را پیدا کنید

راه حل برای مثال 5: تابع f داده شده در بالا ممکن است ضرب توابع (U =( 1 / x - 3 و (V = (x 2 + 3) / (2x - 1در نظر گرفته شود و تابع V ممکن است به عنوان سود دهنده در نظر گرفته شود. دو تابع x 2 + 3 و 2x - 1. ما از قاعده ضرب برای f و قاعده مقدار برای V به شرح زیر استفاده می کنیم

راه حل مشتق به مثال 5 ، مرحله 1