

من فقط فکر کردم که یک تکنیک هوشمندانه را که زمانی برای یافتن مساحت چندضلعی های عمومی استفاده می کردم با شما به اشتراک بگذارم .
چند ضلعی می تواند منظم (همه زوایا مساوی و همه ضلع ها برابرند) یا نامنظم باشد
 |  |
| منظم | بی رویه |
بیایید از این چند ضلعی به عنوان مثال استفاده کنیم:
اولین مرحله این است که هر راس (گوشه) را به یک مختصات تبدیل کنید ، مانند نمودار:
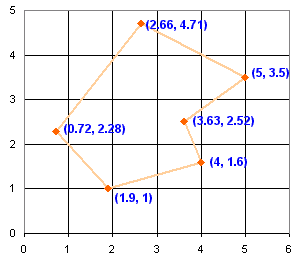
اکنون، برای هر پاره خط، ناحیه پایین تا محور x را مشخص کنید .
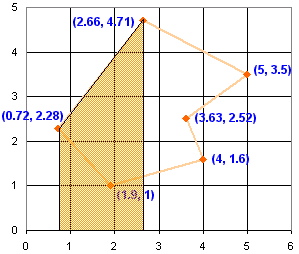
بنابراین، چگونه هر منطقه را محاسبه کنیم؟
مثال: برای شکل برجسته شده در بالا، دو ارتفاع (مختصات "y" 2.28 و 4.71) را می گیریم و ارتفاع متوسط را محاسبه می کنیم:
(2.28+4.71)/2 = 3.495
عرض را محاسبه کنید (تفاوت بین مختصات "x" 2.66 و 0.72)
2.66-0.72 = 1.94
مساحت عرض×ارتفاع است:
1.94 × 3.495 = 6.7803
حالا همه آنها را جمع کنید!
اما ترفند این است که وقتی آنها به جلو می روند (عرض مثبت)، و وقتی به عقب می روند کم می کنیم (عرض منفی).
اگر همیشه در جهت عقربه های ساعت به دور چند ضلعی بروید و همیشه اولین مختصات "x" را از دومی کم کنید، به طور طبیعی انجام می شود، مانند این:
| از جانب | به | |||||
|---|---|---|---|---|---|---|
| ایکس | y | ایکس | y | ارتفاع متوسط | عرض (+/-) | مساحت (+/-) |
| 0.72 | 2.28 | 2.66 | 4.71 | 3.495 | 1.94 | 6.7803 |
| 2.66 | 4.71 | 5 | 3.5 | 4.105 | 2.34 | 9.6057 |
| 5 | 3.5 | 3.63 | 2.52 | 3.01 | -1.37 | -4.1237 |
| 3.63 | 2.52 | 4 | 1.6 | 2.06 | 0.37 | 0.7622 |
| 4 | 1.6 | 1.9 | 1 | 1.3 | -2.1 | -2.7300 |
| 1.9 | 1 | 0.72 | 2.28 | 1.64 | -1.18 | -1.9352 |
| جمع: | 8.3593 | |||||
شما همچنین می توانید به سمت دیگر بروید. اگر یک ناحیه منفی دریافت کردید، آن را مثبت کنید.
و به نظر می رسد این است:
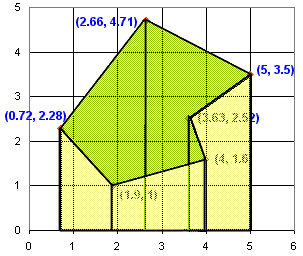
پس همین! مساحت 8.3593 است
محاسبه مساحت یک چند ضلعی می تواند به سادگی یافتن مساحت یک مثلث منتظم یا به پیچیدگی مساحت یک شکل یازده ضلعی نامنظم باشد. اگر می خواهید بدانید که چگونه مساحت چند ضلعی های مختلف را پیدا کنید، فقط این مراحل را دنبال کنید.
مساحت یک ورق تقلب چند ضلعی نامنظم
قسمت1
مساحت چند ضلعی های منتظم را با استفاده از سهم های آنها بیابید
1
فرمول پیدا کردن مساحت چندضلعی منتظم را بنویسید. برای پیدا کردن مساحت یک چند ضلعی منتظم، تنها کاری که باید انجام دهید این است که این فرمول ساده را دنبال کنید: مساحت = 1/2 x محیط xسهم. [1] معنی آن این است:2
سهم چندضلعی را پیدا کنید. اگر از روش سهم استفاده می کنید، سهم برای شما ارائه می شود. فرض کنید با یک شش ضلعی کار می کنید که یک سهم به طول 3√10 دارد.
3
محیط چند ضلعی را پیدا کنید. اگر محیط برای شما فراهم شده باشد، تقریباً کارتان تمام شده است، اما به احتمال زیاد کمی کار بیشتری برای انجام دادن دارید. اگر سهم برای شما ارائه شده است و می دانید که با یک چند ضلعی منظم کار می کنید، می توانید از آن برای پیدا کردن محیط استفاده کنید. در اینجا نحوه انجام آن آمده است:4
سهم و محیط را به فرمول وصل کنید. اگر از ناحیه فرمول = 1/2 x محیط x سهم استفاده می کنید، می توانید 120 را برای محیط و 10√3 را برای سهم وصل کنید. در اینجا به نظر می رسد:5
پاسخ خود را ساده کنید. ممکن است لازم باشد پاسخ خود را به جای جذر مربع به صورت اعشاری بیان کنید. فقط از ماشین حساب خود استفاده کنید تا نزدیکترین مقدار √3 را پیدا کنید و آن را در 600 ضرب کنید. √3 x 600 = 1,039.2. این پاسخ نهایی شماست.
قسمت2
یافتن مساحت چند ضلعی های منتظم با استفاده از فرمول های دیگر
1
مساحت یک مثلث منظم را پیدا کنید. اگر میخواهید مساحت یک مثلث منظم را پیدا کنید، تنها کاری که باید انجام دهید این است که این فرمول را دنبال کنید: مساحت = 1/2 x پایه x ارتفاع.2
مساحت مربع را پیدا کنید. برای پیدا کردن مساحت مربع کافیست طول یک ضلع آن را مربع کنید. این در واقع همان چیزی است که پایه مربع را در ارتفاع آن ضرب کنیم، زیرا پایه و ارتفاع یکسان هستند.3
مساحت یک مستطیل را پیدا کنید . برای پیدا کردن مساحت یک مستطیل، کافی است پایه را در ارتفاع ضرب کنید.4
مساحت ذوزنقه را پیدا کنید. برای پیدا کردن مساحت ذوزنقه، فقط باید این فرمول را دنبال کنید: مساحت = [(پایه 1 + پایه 2) x ارتفاع]/2.قسمت3
پیدا کردن مساحت چند ضلعی های نامنظم
1
مختصات رئوس [3] چندضلعی نامنظم را بنویسید . تعیین مساحت یک چندضلعی نامنظم را زمانی می توان پیدا کرد که مختصات رئوس را بدانید. [4]
2
یک آرایه ایجاد کنید. مختصات x و y هر رأس چند ضلعی را به ترتیب خلاف جهت عقربه های ساعت فهرست کنید. مختصات اولین نقطه در انتهای لیست را تکرار کنید.
3
مختصات x هر راس را در مختصات y راس بعدی ضرب کنید. نتایج را اضافه کنید. جمع اضافه این محصولات 82 می باشد.
4
مختصات y هر راس را در مختصات x راس بعدی ضرب کنید. باز هم این نتایج را اضافه کنید. مجموع اضافه شده این محصولات -38 است.
5
مجموع حاصلضرب های دوم را از مجموع مصنوعات اول کم کنید. 38- را از 82 کم کنید تا 82 - (38-) = 120 به دست آید.
6
این اختلاف را بر 2 تقسیم کنید تا مساحت چندضلعی را بدست آورید. فقط 120 را بر 2 تقسیم کنید تا به 60 برسید و همه چیز تمام است.
در این درس ها یاد خواهیم گرفت
صفحه های مرتبط
ریاضی مسئله های کار
حل کار مسئله های با استفاده از جبر
بیشتر جبر درس
مسئله های کاری کاربردهای مستقیمی در زندگی واقعی دارند. ما اغلب باید تعیین کنیم که برای تکمیل یک کار در یک زمان معین به چند نفر نیاز داریم. از طرف دیگر، با توجه به تعداد محدودی از کارگران، ما اغلب باید تعیین کنیم که چقدر طول می کشد تا یک پروژه به پایان برسد. در اینجا ما با مفاهیم اساسی ریاضی در مورد نحوه رسیدگی به این نوع مسائل سروکار داریم.
فرمول «کار» مسائلی که دو نفر را درگیر میکند ، است 
این فرمول برای بیش از دو نفر قابل تمدید است . همچنین می توان از آن در مسئله هایی استفاده کرد که شامل پر کردن مخزن توسط لوله ها می شود .
مثال 1:
پیتر می تواند چمن را در 40 دقیقه کنده و جان می تواند چمن را در 60 دقیقه کند. چقدر طول می کشد تا آنها چمن را با هم بچینند؟
راه حل:
مرحله 1: تعیین متغیرها :
اجازه دهید x = زمان چمن زنی با هم.
مرحله 2: از فرمول استفاده کنید:![]()
مرحله 3: حل معادله LCM 40 و 60 120 ضرب هر دو طرف با 120
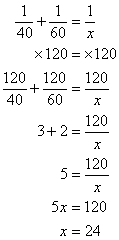
پاسخ: مدت زمانی که هر دوی آنها با هم چمن زنی می کنند 24 دقیقه است.
مثال 2:
چیدن چهل بوشل سیب ماریا 10 ساعت طول می کشد. Kayla می تواند همان مقدار را در 12 ساعت انتخاب کند. اگر با هم کار کنند چقدر طول می کشد؟ پاسخ خود را به نزدیکترین صدم گرد کنید.
مثال 1:
جین، پل و پیتر می توانند نقاشی حصار را در 2 ساعت تمام کنند. اگر جین کار را به تنهایی انجام دهد، می تواند آن را در 5 ساعت تمام کند. اگر پل کار را به تنهایی انجام دهد، می تواند آن را در 6 ساعت تمام کند. چقدر طول می کشد تا پیتر به تنهایی کار را تمام کند؟
راه حل:
مرحله 1: تعیین متغیرها :
اجازه دهید x = زمان صرف شده توسط پیتر
مرحله 2: از فرمول استفاده کنید:![]()
مرحله 3: حل معادله
هر دو طرف را در 30 x ضرب کنید
پاسخ: زمان صرف شده برای پیتر برای رنگ آمیزی حصار به تنهایی ![]() چند ساعت است.
چند ساعت است.
مثال 2:
جیم می تواند در عرض 12 ساعت به تنهایی چاله ای حفر کند. جان می تواند این کار را در 8 ساعت انجام دهد و جک می تواند آن را در 6 ساعت انجام دهد. اگر با هم کار کنند چقدر طول می کشد؟
مثال 1:
یک مخزن را می توان با لوله A در 3 ساعت و توسط لوله B در 5 ساعت پر کرد. هنگامی که مخزن پر شد، می توان آن را توسط لوله C در 4 ساعت تخلیه کرد. اگر مخزن ابتدا خالی باشد و هر سه لوله باز باشد، چند ساعت طول می کشد تا باک پر شود؟
راه حل:
مرحله 1: اختصاص متغیرهای :
اجازه دهید X = زمان گرفته شده را پر کنید تا مخزن
مرحله 2: از فرمول استفاده کنید:
از آنجایی که لوله C آب را تخلیه می کند، کم می شود.![]()
مرحله 3: معادله را حل کنید
LCM از 3، 4 و 5 60 است
هر دو طرف را در 60 ضرب کنید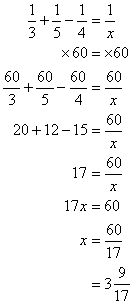
پاسخ: مدت زمان پر کردن مخزن ![]() ساعت است.
ساعت است.
مثال 2:
لوله 1 5 روز طول می کشد تا استخر را تخلیه کند و لوله 2 7 روز طول می کشد تا استخر را تخلیه کند. چقدر طول می کشد تا این دو لوله با هم آب استخر را تخلیه کنند؟
وقتی دو نفر در حال انجام یک کار با هم با حل سیستم معادلات هستند، می توان مسائل ای را حل کرد. برای حل یک مشکل کاری، نرخ ساعتی کار دو نفر با هم را در زمان صرف شده برای کار ضرب کنید تا کل زمان صرف شده برای کار را بدست آورید. دانش حل سیستم معادلات برای حل این نوع مسائل ضروری است.
مثال:
لاتیشا و ریکی برای یک شرکت نرم افزار کامپیوتری کار می کنند. آنها با هم می توانند یک برنامه کامپیوتری خاص را در 19 ساعت بنویسند. لاتیشا می تواند در 32 ساعت برنامه را خودش بنویسد. چه مدت طول می کشد تا ریکی برنامه را به تنهایی بنویسد؟
مثال:
یک استخر شنا از طریق زهکشی در پایین استخر تخلیه می شود و توسط شیلنگ در بالا پر می شود. اگر شیلنگ بتواند استخر را در 21 ساعت پر کند و زهکشی ظرف 24 ساعت استخر را خالی کند، اگر در باز بماند چند ساعت طول می کشد تا استخر را پر کند؟ پاسخ را بر حسب ساعت بیان کنید و در صورت نیاز پاسخ را به نزدیکترین ساعت گرد کنید.

فیزیک دوچرخه موضوعی گسترده و پیچیده است، شاید بیش از آن چیزی که بتوان تصور کرد. اگرچه تعداد اجزای یک دوچرخه کم است، اما تعامل بین آنها و اصول دینامیکی درگیر، پیچیده است. این امر به ویژه در مورد پایداری دوچرخه، که نتیجه یک تعامل پویا پیچیده در سیستم دوچرخه سواری است، صادق است.
در این صفحه برخی از جنبههای اصلی فیزیک دوچرخهها را توضیح خواهم داد، که باید به خواننده درک بیشتری از نحوه کار دوچرخهها از منظر فیزیک بدهد.
فیزیک دوچرخه - پایداری
دوچرخه ها به طور ذاتی در هنگام سواری پایدار هستند. حتی دوچرخه های بدون سوار نیز اگر سرعت کافی به جلو داشته باشند، پایدار هستند. تلاش زیادی برای تجزیه و تحلیل عواملی که باعث پایداری دوچرخه می شوند انجام شده است. مشخص شده است که "مسیر" (در زیر نشان داده شده است) اغلب نقش مهمی در پایداری دوچرخه دارد. برای طراحی سنتی دوچرخه، اگر مسیر مثبت باشد، به این معنی که محور فرمان با زمین جلوتر از نقطه تماس چرخ جلو و زمین باشد، دوچرخه در هنگام سواری پایدارتر است (یعنی احتمال سقوط آن کمتر است. هنگام سوار شدن بر آن). اگر این برجستگی در پشت نقطه تماس (دنباله منفی) باشد، دوچرخه پایداری کمتری دارد و احتمال سقوط دوچرخه هنگام سوار شدن بر آن بیشتر است.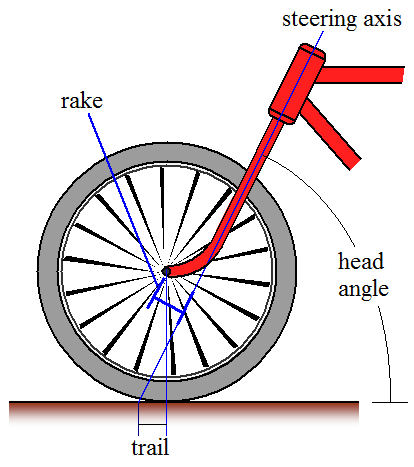
بر اساس پارامترهای هندسی نشان داده شده، فرمول ریاضی برای دنباله:
که در آن R W شعاع چرخ است، ساعت زاویه سر است که به عنوان نشان داده شده است، و ای اف با چنگک جمع کردن است، به عنوان نشان داده شده است، همچنین به عنوان چنگال جبران شناخته شده است.
هنگام تجزیه و تحلیل پایداری دوچرخه، استفاده از دو پارامتر رایج است. زاویه انحراف و زاویه فرمان دوچرخه. زاویه انحراف، زاویه چپ و راست قاب دوچرخه با صفحه عمودی است، و زاویه فرمان، زاویه ای است که چرخ جلو با صفحه دوچرخه (شامل قاب دوچرخه) ایجاد می کند. شکل زیر زاویه انحراف و فرمان را نشان می دهد.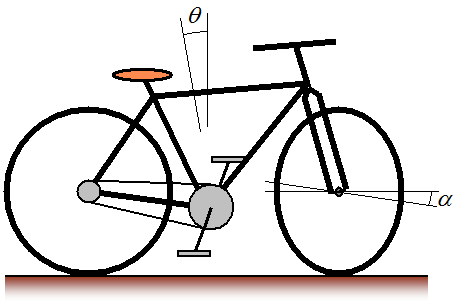
که در آن θ زاویه ناب و α زاویه فرمان است. قرارداد علامت برای این زوایا معمولاً به شرح زیر است و با توجه به سواری که روی دوچرخه نشسته است: سمت راست θ مثبت و چپ چپ منفی θ است . فرمان راست α مثبت و فرمان چپ α منفی است. برای تجزیه و تحلیل پایداری، هر دوی این زوایا تنها متغیرهای مستقل مورد نیاز برای تجزیه و تحلیل ریاضی پایداری دوچرخه هستند. آنها به طور کامل جهت دوچرخه را در هنگام حرکت در جهت جلو توصیف می کنند. برای اینکه یک دوچرخه ثابت باشد، زاویه فرمان و لجن باید تمایل به خاموش شدن داشته باشند، به این معنی که این زوایا در اطراف صفر با مقادیر مثبت و منفی کوچک نوسان می کنند. این به نوبه خود به این معنی است که دوچرخه تمایل دارد با چرخش کمی عمودی بماند، در حالی که در جهت جلو حرکت می کند. جالب است که قفل کردن فرمان جلو همیشه باعث سقوط دوچرخه می شود. فیزیک پایداری مستلزم آن است که چرخ جلو بتواند آزادانه هدایت کند.
همانطور که گفته شد، تجزیه و تحلیل پایداری دوچرخه یک کار پیچیده است که شامل معادلات بزرگ و "درهم" است. فعل و انفعالات فیزیکی زیادی بین اجزای مختلف دوچرخه (یعنی چرخ جلو و عقب، ستون فرمان و قاب دوچرخه) وجود دارد که امکان توضیح کاملاً شهودی را فراهم می کند. برای به دست آوردن درک قابل توجهی از پایداری دوچرخه، بهتر است یک تحلیل دینامیک کامل انجام دهید و سپس درک خود را بر اساس نتایج این تجزیه و تحلیل قرار دهید.
تجزیه و تحلیل پایداری دوچرخه با استفاده از یک فرض "بی سوار" معمول است. این بدان معناست که دوچرخه فقط با دوچرخه به تنهایی (بدون سوار) مدل شده است. این امر تجزیه و تحلیل را بسیار ساده می کند، و در نتیجه اغلب فرض می شود که یک دوچرخه ثابت بدون سوار با حضور یک سوار نیز پایدار خواهد بود. این می تواند یک فرض معقول باشد اما متأسفانه "ورودی" راکب را نادیده می گیرد که بر پایداری دوچرخه در طول استفاده نیز تأثیر می گذارد.
با این وجود، در غیاب چیزی بهتر، انجام آنالیزهای پایداری روی دوچرخههای بدون سوار معمول است. اگر میخواهید تحلیل کامل دوچرخههای بدون سوار را ببینید، مقاله زیر را ببینید:
معادلات دینامیک خطی برای تعادل و هدایت دوچرخه: یک معیار و بررسی, JP Meijaard, Jim M. Papadopoulos, Andy Ruina, AL Schwab, ژوئن 2007.
اثرات ژیروسکوپی بر پایداری دوچرخه
باور رایج این است که اثرات ژیروسکوپی به خودی خود چیزی است که دوچرخه را پایدار می کند. این در واقع اینطور نیست. اگرچه جلوههای ژیروسکوپی نقشی را ایفا میکنند، اما صرفاً بخشی از یک تعامل دینامیکی بسیار بزرگتر هستند که بین اجزای مختلف دوچرخه اتفاق میافتد، که در مجموع همان چیزی است که در نهایت دوچرخه را در حین دوچرخهسواری پایدار میکند. طراحی یک دوچرخه، و پیکربندی اجزای مختلف، در طول اعصار (عمدتاً از طریق آزمون و خطا) بهینه شده است تا آن را تا حد امکان پایدار کند.
همانطور که گفته شد، جلوه های ژیروسکوپی سهم اصلی در پایداری دوچرخه نیست، اما هنوز هم آموزنده است که ببینید چگونهاثرات ژیروسکوپی به پایداری کمک می کند. برای درک این سهم، سناریوی زیر را در نظر بگیرید:
فرض کنید یک دوچرخه بدون سوار با سرعت خاصی حرکت می کند. بیایید بیشتر بگوییم که دوچرخه به سمت راست خم می شود ( θ مثبت ). این باعث می شود چرخ جلو به راست هدایت شود ( α مثبت) به دلیل اثر ژیروسکوپی. برای کمک به درک اینکه چرا این اتفاق میافتد، به این فکر کنید که برای جلوگیری از فرمانپذیری چرخ جلو به سمت راست چه باید کرد. برای جلوگیری از هدایت چرخ جلو به سمت راست، باید گشتاوری را در جهت چپ (برعکس) روی فرمان اعمال کنید. بنابراین، با نبود گشتاور (در دوچرخه بدون سوار)، چرخ جلو به طور طبیعی به سمت راست هدایت می شود. شما می توانید این را خودتان با دوچرخه امتحان کنید. دوچرخه را از روی زمین بلند کنید و به سرعت چرخ جلو را در جهت جلو بچرخانید. سپس، قاب دوچرخه را کمی به چپ یا راست متمایل کنید و ببینید در پاسخ چه اتفاقی برای چرخ جلو می افتد. این را با اتفاقی که هنگام چرخاندن چرخ جلو، هنگام کج کردن دوچرخه روی میدهد، مقایسه کنید.
با چرخاندن فرمان به سمت راست، دوچرخه در یک مسیر دایره ای (به سمت راست) حرکت می کند. این باعث کاهش θ می شودبه دلیل تأثیر شتاب مرکزگرا. این به نوبه خود باعث می شود دوچرخه به سمت چپ خم شود ( θ منفی ) که باعث می شود چرخ جلو به سمت چپ هدایت شود ( α منفی )، که سپس باعث می شود دوچرخه در یک مسیر دایره ای (به سمت چپ) حرکت کند. شتاب گریز از مرکز این باعث کاهش θ (دوچرخه به سمت راست می شود) می شود که دوباره باعث می شود چرخ جلو به راست هدایت شود و روشن و روشن شود. اگر دوچرخه در ابتدا به چپ خم شود، زنجیرهای از رویدادها اتفاق میافتد ( θ منفی ). این زنجیره رویدادها از سقوط دوچرخه جلوگیری می کند.
کل فعل و انفعالات فیزیکی در حال وقوع در واقع پیچیده تر از سناریوی بالا هستند، به خصوص به دلیل نوسانات θ و α.. اما سناریوی سادهشدهای که در بالا ارائه شد، نقش تأثیرگذاری ژیروسکوپی را در پایدار نگه داشتن دوچرخه نشان میدهد.
Leaning Into A Turn
منبع: http://en.wikipedia.org/wiki/Bicycle_and_motorcycle_dynamics. نویسنده: http://en.wikipedia.org/wiki/User:Furmanj
هنگام دوچرخه سواری، برای جبران اثر شتاب مرکزگرا، باید به یک پیچ خم شوید. انحراف به سمت داخل شتاب مرکزگرا را متعادل می کند که چرخش را بدون افتادن ممکن می کند.
برای تجزیه و تحلیل فیزیک پشت ناب، شماتیک زیر را در نظر بگیرید.
جایی که:
θ زاویه ناب است
R شعاع پیچ اندازه گیری شده از مرکز جرم G سیستم دوچرخه سواری است.
ج است شتاب مرکزگرا از مرکز جرم G از سیستم دوچرخه سوار
متر است که جمعی از سیستم دوچرخه سوار
گرم شتاب به دلیل گرانش، بر روی زمین، که 9.8 متر است / s را 2
L فاصله است از نقطه G به نقطه تماس موثر P بین دوچرخه و زمین
N نیروی نرمال بین دوچرخه و زمین است
F نیروی اصطکاک بین دوچرخه و زمین است، در جهت ج از آنجا که هیچ شتاب در جهت عمودی مجموع وجود دارد نیروهای عمودی صفر است. بدین ترتیب،
قانون دوم نیوتن را در جهت افقی اعمال کنید:
که در آن v سرعت دوچرخه در اطراف پیچ است.
لحظه های مربوط به نقطه G را جمع کنید :
(توجه داشته باشید که اثرات سه بعدی را در این معادله نادیده می گیریم. آنها ناچیز فرض می شوند).
سه معادله بالا را با هم ترکیب کنید تا یک عبارت برای زاویه θ لاغر پیدا کنید . ما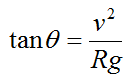
در بخش بعدی ما در نیروها و قدرت.
نیروها و نیرو
در شکل زیر دوچرخه ای را نشان می دهد که در سربالایی با زاویه شیب Φ و با سرعت V حرکت می کند .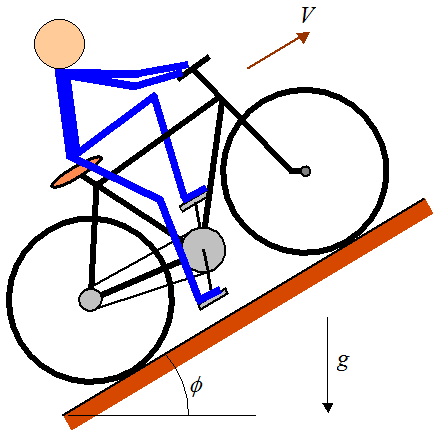
برای به حرکت درآوردن دوچرخه در سربالایی، دوچرخه سوار باید پدال ها را فشار دهد. پدالها 180 درجه جابجا شدهاند، به این معنی که تنها یک پدال را میتوان در یک زمان، از موقعیت بالا به پایین، و سپس به پدال دیگر سوئیچ کرد.
با توجه به نیروی F 1 که بر روی پدال وارد می شود، می توانیم نیروی حاصل از F 4 را بین چرخ عقب و زمین محاسبه کنیم. این نیرویی است که دوچرخه را به جلو می راند.
بر اساس این فرض که شتاب (خطی و زاویه ای) ناچیز است، می توانیم تحلیل گشتاور را با دقت خوبی انجام دهیم. از این رو، می توانیم این را به عنوان یک مشکل ثابت در نظر بگیریم.
شکل زیر را با نیروها و ابعاد شعاعی در نظر بگیرید.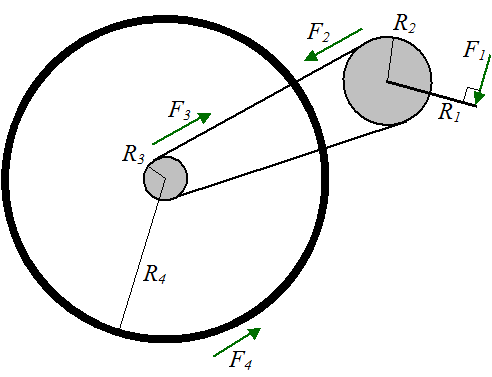
کجا:
F 1نیروی اعمال شده به پدال است
R 1 شعاع پدال است
F 2 نیروی وارد بر میل لنگ اصلی، با توجه به زنجیره مخاطب
R 2 است میل لنگ شعاع اصلی
F 3 نیروی وارد بر دنده عقب است، به علت تماس های زنجیره ای
R 3 شعاع چرخ دنده عقب است
F 4 نیرویی است که بر چرخ عقب در اثر تماس با زمین وارد می شود. توجه داشته باشید که ضریب اصطکاک استاتیکی بین چرخ و زمین باید به اندازه کافی بزرگ برای حمایت از این نیروی شود، در غیر این صورت لغزش رخ می دهد
R 4 شعاع چرخ عقب است
با استفاده از فرض تعادل ایستا، میتوانیم معادلات گشتاور زیر را بنویسیم:![]()
و![]()
از آنجایی که F 2 = F 3 ، میتوانیم دو معادله بالا را ترکیب کنیم تا بیانی برای F 4 بدست آوریم :
نیروی F 4 چیزی است که دوچرخه را به جلو میبرد. اگر فرض کنیم دوچرخه با سرعت ثابت (بدون شتاب) حرکت می کند، نیروی F 4 باید با نیروهای مقاومت مخالف حرکت دوچرخه برابر باشد. این نیروهای مقاوم عبارتند از: جاذبه، مقاومت غلتشی، کشش هوا و اصطکاک داخلی دوچرخه. اگر از دومی غافل شویم، میتوانیم عبارت ریاضی زیر را بنویسیم:
کجا:
Fنیرویی است که دوچرخه را به جلو می راند. توجه داشته باشید که F ≡ F 4
C r ضریب مقاومت غلتشی است که می تواند 0.0022 تا 0.005 برای لاستیک دوچرخه باشد (رجوع کنید: http://en.wikipedia.org/wiki/Rolling_resistance)
C d ضریب درگ
ρ است. چگالی هوایی که دوچرخه از طریق آن حرکت می کند
A سطح مقطع پیش بینی شده دوچرخه + راکب عمود بر جهت جریان (یعنی عمود بر v ) است و v سرعت دوچرخه نسبت به هوا است.
اولین عبارت در سمت راست معادله فوق سهم گرانش است. اصطلاح دوم سهم مقاومت غلتشی است. سومین عبارت سهم کشش هوایی است.
برای ارزیابی توان P مورد نیاز برای به حرکت درآوردن دوچرخه، معادله فوق را در v ضرب کنید . ما P = پارامتر Fv ، و
برای یک سطح صاف (بدون شیب) مجموعه Φ = 0. ما
و
ما همچنین می توانید برای سرعت حد یک دوچرخه در سرازیری به پایین تپه با زاویه تمایل داده شده از حل Φ . از آنجایی که سوارکار در این حالت هیچ نیرویی به پدال ها وارد نمی کند، F ≡ F 4 داریم.= 0. بنابراین، نیروی گرانش باید نیروهای مقاومتی ناشی از مقاومت غلتشی و کشش هوا را متعادل کند. از این رو، میتوانیم سرعت کوستینگ پایانی v را در معادله زیر حل کنیم:
طبیعتاً، هنگام دوچرخهسواری میخواهیم نیروهای مقاومتی مخالف حرکت را تا حد امکان پایین نگه داریم. این امر با تحت فشار قرار دادن لاستیک ها (که مقاومت غلتشی را به حداقل می رساند) و کوچک نگه داشتن ناحیه جلویی A تا حد امکان برای کاهش کشش هوا انجام می شود، به خصوص هنگام سفر با سرعت بالا، مانند مسابقه. به طور معمول، مقاومت غلتشی بسیار بالاتر از کشش هوا است، بنابراین کاهش A برای سوارکاری معمولی که با سرعت متوسط حرکت می کند مهم نیست.
یک آزمایش سرگرم کننده
این آزمایش جالب مربوط به فیزیک دوچرخه را امتحان کنید (در زیر نشان داده شده است). دوچرخه را به صورت عمودی بایستید و یکی از پدال ها را طوری جهت دهید که در پایین قرار گیرد. بعد، پدال را به چپ فشار دهید. دوچرخه به کدام سمت حرکت می کند؟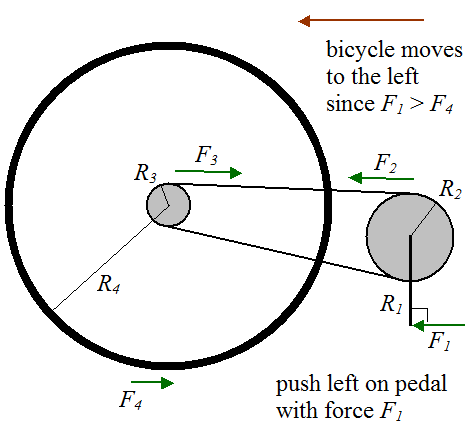
پاسخ: دوچرخه به سمت چپ حرکت می کند (که ممکن است برای شما غیر شهودی باشد). حتی اگر نیرویی که به پدال وارد میکنید، میل لنگ اصلی را در جهت عقربههای ساعت میچرخاند، که جهت مورد نیاز برای حرکت دوچرخه به سمت راست است، دوچرخه در نهایت به سمت چپ حرکت میکند. این به این دلیل است که نیروی خارجی F 1 که به دوچرخه وارد می کنید، منجر به نیروی کمتری F 4 در جهت مخالف می شود. از F 1 > F 4، دوچرخه به سمت چپ حرکت می کند. حال، اگر بخواهید روی دوچرخه بنشینید و با پای خود نیروی F 1 را اعمال کنید، دوچرخه به سمت راست حرکت می کند زیرا F 1 اکنون یک نیروی داخلی در سیستم دوچرخه سوار است و بنابراین تنها نیروی خارجی است که بر روی دوچرخه وارد می شود. دوچرخه F 4 است که روی چرخ عقب عمل می کند و دوچرخه را به سمت راست هل می دهد.
منبع
https://www.real-world-physics-problems.com/bicycle-physics.html
چند ضلعی
چند ضلعی به یک شکل دوبعدی بسته اشاره دارد که از تعداد محدودی پاره خط تشکیل شده است . تعداد رئوس یک چند ضلعی همیشه برابر با تعداد پاره های خط است. نمونه هایی از چند ضلعی ها عبارتند از:
محیط یک چند ضلعی
مجموع فاصله اضلاع بیرونی یک شکل بسته به عنوان محیط شناخته می شود . طول کل تمام ضلع های یک چند ضلعی است.
محیط = مجموع همه اضلاع |
واحد محیط هر چند ضلعی مانند واحد اضلاع مربوطه خود باقی می ماند. اگر اضلاع در واحدهای مختلف داده شده اند، آنها را به یک واحد تبدیل کنید و سپس محیط را پیدا کنید.
یک چند ضلعی منتظم همه اضلاع برابر است. بنابراین، می توانیم محیط یک چند ضلعی منظم را با جمع مکرر پیدا کنیم. بنابراین، اگر ضلع های n در چند ضلعی وجود داشته باشد، همان طول 'n' را اضافه می کنیم.
محیط چند ضلعی منتظم = (طول یک ضلع) × تعداد اضلاع |
مثال 1 : محیط شش ضلعی منتظم با ضلع 4 سانتی متری را پیدا کنید.

محیط یک چند ضلعی منظم = (طول یک ضلع) × تعداد اضلاع
محیط یک شش ضلعی منظم = 4 سانتی متر × 6
= 24 سانتی متر
مثال 2 : یک پنج ضلعی همه اضلاع برابر با 6 سانتی متر است. محیط آن چقدر خواهد بود؟

تمام اضلاع پنج ضلعی برابر است. بنابراین، یک چند ضلعی منظم است.
محیط یک چند ضلعی منظم = (طول یک ضلع) × تعداد اضلاع
محیط یک پنج ضلعی منظم = 6 × 5 سانتی متر
= 30 سانتی متر
این فاصله کل دور یک چند ضلعی است. با جمع کردن تمام اضلاع چند ضلعی می توان آن را پیدا کرد.
مثال 1 : محیط مستطیل زیر را محاسبه کنید:

محیط = مجموع همه اضلاع
محیط مستطیل = طول + عرض + طول + عرض
محیط مستطیل = 15 سانتی متر + 7 سانتی متر + 15 سانتی متر + 7 سانتی متر = 44 سانتی متر
بنابراین، فرمول محیط یک مستطیل:
| محیط = 2 × طول + عرض |
مثال 2 : محیط چند ضلعی زیر را محاسبه کنید:

محیط = مجموع طول همه اضلاع
= 13 سانتی متر + 3.5 سانتی متر + 3.5 سانتی متر + 13 سانتی متر + 4 سانتی متر = 37 سانتی متر
مثال 5 : مساحت یک مربع به عنوان 100 سانتی متر داده 2 . محیط آن را بیابید.
مساحت مربع = 100 سانتی متر 2
فرمول مساحت مربع = سمت ضلع
به عنوان، 100 = سمت جانبی
بنابراین، Side = 10 سانتی متر است
محیط یک مربع = ضلع + ضلع + ضلع + ضلع = 4 ضلع
= 4×10=40 سانتی متر
حقایق جالب
|
 چگونه محیط چند ضلعی را پیدا کنیم؟
چگونه محیط چند ضلعی را پیدا کنیم؟
 فرمول محیط چند ضلعی چیست؟
فرمول محیط چند ضلعی چیست؟
 چگونه محیط یک چند ضلعی منظم با n ضلع را پیدا کنیم؟
چگونه محیط یک چند ضلعی منظم با n ضلع را پیدا کنیم؟
 محیط را در موقعیت های واقعی از کجا پیدا کنیم؟
محیط را در موقعیت های واقعی از کجا پیدا کنیم؟
پاسخ صحیح را انتخاب کنید
1. چهار ضلع یک شش ضلعی نامنظم 5 سانتی متر است. اندازه های دو ضلع دیگر 6 سانتی متر و 7 سانتی متر است. محیط شش ضلعی چقدر است؟
30 سانتی متر
33 سانتی متر
26 سانتی متر
34 سانتی متر
بررسی
2. یکی از اضلاع یک پنج ضلعی منظم 6 سانتی متر است. محیط پنج ضلعی چقدر است؟
30 سانتی متر
42 سانتی متر
36 سانتی متر
24 سانتی متر
بررسی
3. یک چند ضلعی نامنظم با سه ضلع اندازه اضلاع آن 4 سانتی متر، 8 سانتی متر و 6 سانتی متر است. محیط چند ضلعی چقدر است؟
6 سانتی متر
24 سانتی متر
12 سانتی متر
18 سانتی متر
بررسی
4. یک مستطیل دارای طولی برابر با 7 سانتی متر و عرض آن برابر با 9 سانتی متر است. محیط مستطیل چقدر است؟
63 سانتی متر
16 سانتی متر
32 سانتی متر
2 سانتی متر
[1-H][M+5]+75i+7k=4
:این یک معادله با 4 مجهولی است و مجهولات عبارتند از
H,M,i,k
در این معادله درجه آزادی 3 است
یعنی با دادن سه مقدار به سه مجهول می توان یک مجهول دیگر را بدست آورد
 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.