دل نوشته ها ی نقش و آموزش ریاضی  

f:{7,8,9,10,11} --->{14,16,18,20,22}

f(x)=2x

g:{14,16,18,20,22}---->{7,8,9,10,11}

g(t)=./5t

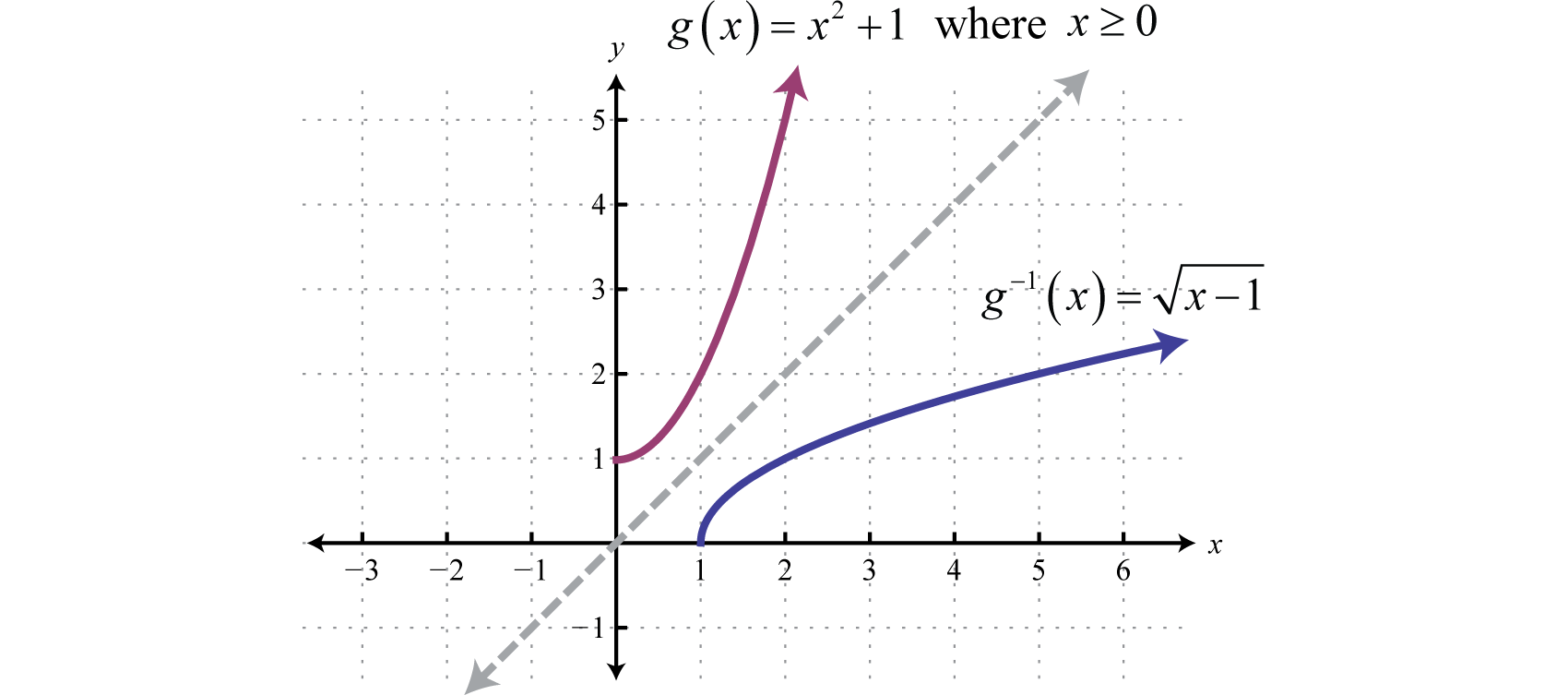
نمودار معکوس یک تابع قرینه ی آن نسبت به نیمساز ربع اول و سوم است

این یک فرمول اساسی از تئوری مجموعه ها است. برای مجموعه A، n(A) تعداد عناصر موجود در آن را نشان می دهد. نمودار ون فرمول رابطه بین تعداد عناصر از دو مجموعه می دهد. توسط:

n(A UB) = n(A) + n(B) – n (A ⋂ B)

اینجا،

• n(A UB) تعداد عناصر موجود در یکی از مجموعه های A یا B را نشان می دهد
• n (A ⋂ B) تعداد عناصر موجود اساساً در هر دو مجموعه A و B را نشان می دهد

اجازه دهید کاربردهای فرمول نمودار ون را در بخش زیر ببینیم.

مثال های حل شده با استفاده از فرمول نمودار ون

1. مثال 1:  در یک کلاس 70 دانش آموز، 45 دانش آموز دوست دارند فوتبال بازی کنند. 52 دانش آموز دوست دارند بیسبال بازی کنند. همه دانش آموزان دوست دارند حداقل یکی از این دو بازی را انجام دهند. چند دانش آموز دوست دارند فوتبال یا بیسبال بازی کنند؟ چند دانش آموز دوست دارند فقط فوتبال بازی کنند؟

   راه حل:   اطلاعات داده شده را می توان با نمودارهای ون به صورت زیر نشان داد.

   

   فرض کنید n (A ⋂ B) = x، n(A) = 45، n(B) = 52،

   می دانیم که n(AUB) = 70

   با استفاده از فرمول نمودار ون،

   n(A ⋂ B) = x = n(A) + n(B) - n(AUB)

   = 45 + 52 - 70 = 27

   دانش آموزانی که دوست دارند فقط فوتبال بازی کنند = 45 - 27 = 18

   پاسخ: 27 دانش آموز دوست دارند فوتبال یا بیسبال بازی کنند و 18 دانش آموز دوست دارند فقط فوتبال بازی کنند.

2. مثال 2:  100 دانش آموز هستند که 35 نفر نقاشی و 45 نفر رقصند. 10 هر دو را لایک می کنند. چند نفر از دانش آموزان یکی از آنها را دوست دارند یا هیچ کدام را؟

   راه حل:  تعداد کل دانش آموزان = 100

   تعداد دانش آموزانی که نقاشی را دوست دارند، n (P) = 35

   تعداد دانش آموزانی که رقصیدن را دوست دارند، n(D) = 45

   تعداد دانش آموزانی که هر دو را دوست دارند، n(P∩D) = 10

   تعداد دانش آموزانی که با استفاده از فرمول نمودار ون یکی از آنها را دوست دارند،

   n(PUD) = n(P) + n(D) – n(P∩D)

   ⇒ 45 + 35 - 10 = 70

   تعداد دانش آموزانی که هیچکدام را دوست ندارند = کل دانش آموزان - n (PUD) = 100 - 70 = 30          

   پاسخ: 70 دانش آموز هر کدام را دوست دارند و 30 دانش آموز هیچ کدام را دوست ندارند.