صل شمول-استخراج: مثال هایی با راه حل ها
بر: 21 نوامبر 2018
درک کامل اصل شمول-حذف در ریاضیات گسسته برای ایجاد یک پایه محکم در نظریه مجموعه ها حیاتی است.
با اصل گنجاندن-خروج، به طور کلی دو نوع سوال در برنامه های درسی ریاضیات گسسته مقدماتی و سطح پایین وجود دارد. این انواع سوالات عبارتند از:
- تعداد عناصر در مجموعه های خاص و همچنین تعداد عناصر موجود در تقاطع های مجموعه مشخص داده شده است. سپس لازم است تعداد عناصری که در یک مجموعه یا زیرمجموعه معین زندگی می کنند - به استثنای مجموعه های دیگر - تعیین شود. (از این رو، بخش «حذف» این اصل است.)
- نوع دوم پیچیده تر است. تعداد عناصر ساکن در تقاطع مجموعه ها ناشناخته است و نیاز به تعیین دارد. به این مجهول یک عدد جبری (مانند x ) داده می شود و سپس به صورت جبری حل می شود. سه مجموعه اغلب درگیر هستند.
در این مقاله، چندین مثال و راهحل اصل گنجاندن-خروج را برای هر دو نوع مورد بحث قرار خواهیم داد. نمودارهای ون، اگرچه ضروری نیستند، برای کمک به مفهوم سازی گنجانده شده اند.
اصل شمول-حذف: مثال یک (دو مجموعه)
سوال:
از میان 50 بیمار بستری شده در بیمارستان، 25 نفر مبتلا به ذات الریه، 30 نفر مبتلا به برونشیت و 10 نفر با هر دو ذات الریه و برونشیت تشخیص داده شده اند. تعیین کنید:
الف) تعداد بیمارانی که پنومونی یا برونشیت (یا هر دو) تشخیص داده شده است.
(ب) تعداد بیمارانی که پنومونی یا برونشیت تشخیص داده نشده است.
راه حل:
اولین قدم شناسایی رسمی مجموعه ها و نشان دادن تعداد عناصر در هر یک است. این را می توان صرفاً با اطلاعات داده شده انجام داد. هیچ محاسبه ای لازم نیست. با این سوال اصل شمول-حذف، سه مجموعه را می توان به صورت زیر تعریف کرد:
اجازه دهید U کل مجموعه بیماران را نشان دهد. اجازه دهید P و B به ترتیب مجموعه بیمارانی را که پنومونی و برونشیت تشخیص داده اند نشان دهند. بدین ترتیب:
|U| = 50
|P| = 25
|B| = 30
|P ∩ B| = 10
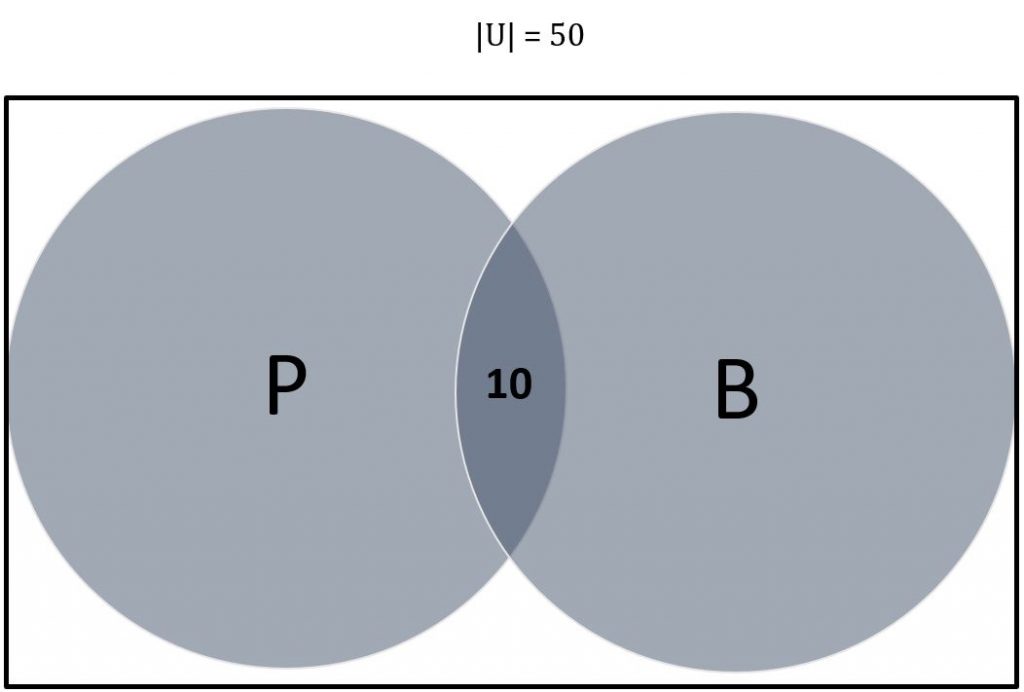
اکنون ممکن است یک نمودار ون ایجاد کنیم. دو مجموعه و در نتیجه دو دایره وجود دارد. از آنجایی که تعداد عناصر موجود در تقاطع P و B را می دانیم ( |P ∩ B| ) ابتدا می توانیم این را پر کنیم:
اکنون می توانیم محاسبه کنیم که چند عنصر فقط در P زندگی می کنند اما نه |P ∩ B|:
از آنجایی که
|P| = 25 و |P ∩ B| = 10، 15
عنصر
(25-10 = 15)
منحصر به P وجود دارد.
برای محاسبه تعداد عناصری که فقط در B زندگی می کنند اما نه |P ∩ B| از همین روش استفاده کنید:
از آنجایی که
|B| = 30 و |P ∩ B| = 10، 20
عنصر
(30-10 = 20)
منحصر به B وجود دارد.
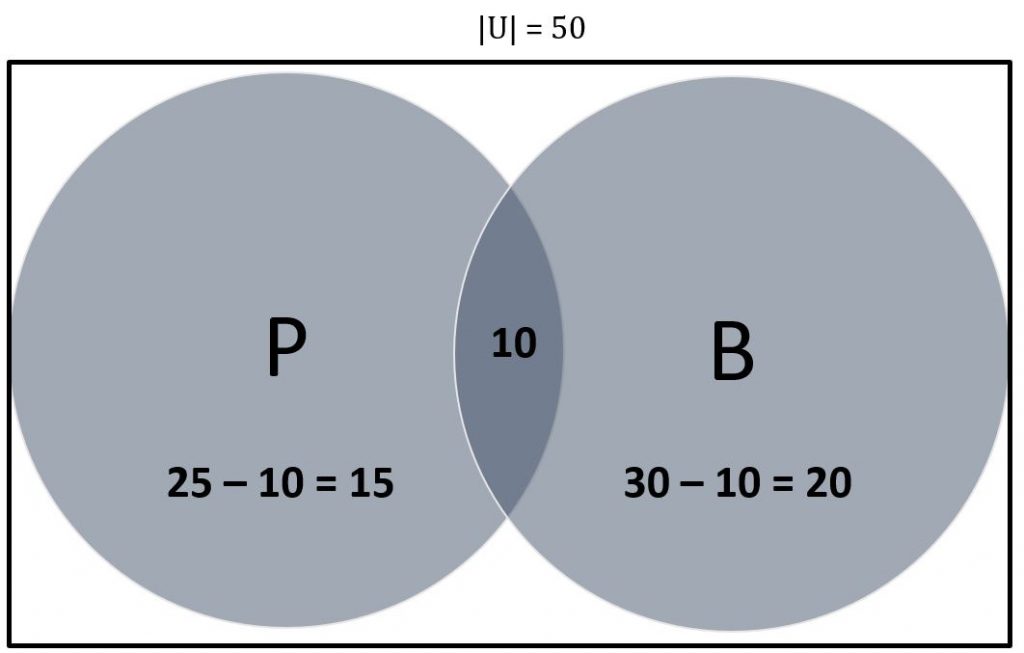
این اطلاعات جدید باید به شکل زیر به نمودار ون اضافه شود:
کار مقدماتی کامل است و ما اطلاعات کافی برای پاسخگویی مستقیم به سوالات داریم:
(الف) تعداد بیماران مبتلا به پنومونی یا برونشیت (یا هر دو) را تعیین کنید .
این همان درخواست برای تعیین |P ∪ B| است. با نگاهی به نمودار ون، پاسخ را به صورت زیر فرموله کنید:
|P ∪ B| = 15 + 10 + 20
= 45
بنابراین 45 بیمار مبتلا به پنومونی یا برونشیت تشخیص داده می شوند.
همین پاسخ را می توان با استفاده از اصل گنجاندن-استخراج مستقیماً بدون مراجعه به نمودار ون نیز بدست آورد:
|P ∪ B| = |P| + |B| – |P ∪ B|
= (25 + 30) - (10)
= 45
بنابراین 45 بیمار مبتلا به پنومونی یا برونشیت تشخیص داده می شوند.
(ب) تعداد بیمارانی که پنومونی یا برونشیت تشخیص داده نشده اند را تعیین کنید.
این همان درخواست برای تعیین |(P ∪ B)'| است. ما می دانیم که در مجموع 50 بیمار وجود دارد - از این تعداد 45 نفر مبتلا به پنومونی یا برونشیت هستند. از این برای حل این سوال استفاده کنید:
|U| = 50.
|P ∪ B| = 45
از این رو،
|(P ∪ B)'|
= 50 - 45 = 5
5 بیمار مبتلا به پنومونی یا برونشیت تشخیص داده نشده اند.
اصل گنجاندن-استخراج: مثال دو (سه مجموعه)
سوال:
یک شرکت بزرگ توسعه نرم افزار 100 برنامه نویس کامپیوتر را استخدام می کند. از این تعداد 45 نفر به جاوا، 30 نفر به سی شارپ، 20 نفر به زبان پایتون، شش نفر به زبان سی شارپ و جاوا، یک نفر به زبان جاوا و پایتون، پنج نفر به زبان سی شارپ و پایتون و تنها یک برنامه نویس به هر سه زبان فوق مسلط است.
تعداد برنامه نویسان کامپیوتری که به هیچ یک از این سه زبان تسلط ندارند را مشخص کنید.
راه حل:
همانطور که در اولین مسئله تمرین اصل گنجاندن در بالا انجام شد، با تعریف اطلاعات داده شده شروع کنید:
اجازه دهید U مجموعه ای از تمام برنامه نویسان کامپیوتری را نشان دهد و اجازه دهید J، C و P به ترتیب نشان دهنده مجموعه برنامه نویسان مسلط به جاوا، سی شارپ و پایتون باشند. بدین ترتیب:
|U| = 100
|J| = 45
|C| = 30
|پ| = 20
|J ∩ C| = 6
|J ∩ P| = 1
|C ∩ P| = 5
|J ∩ C ∩ P| = 1
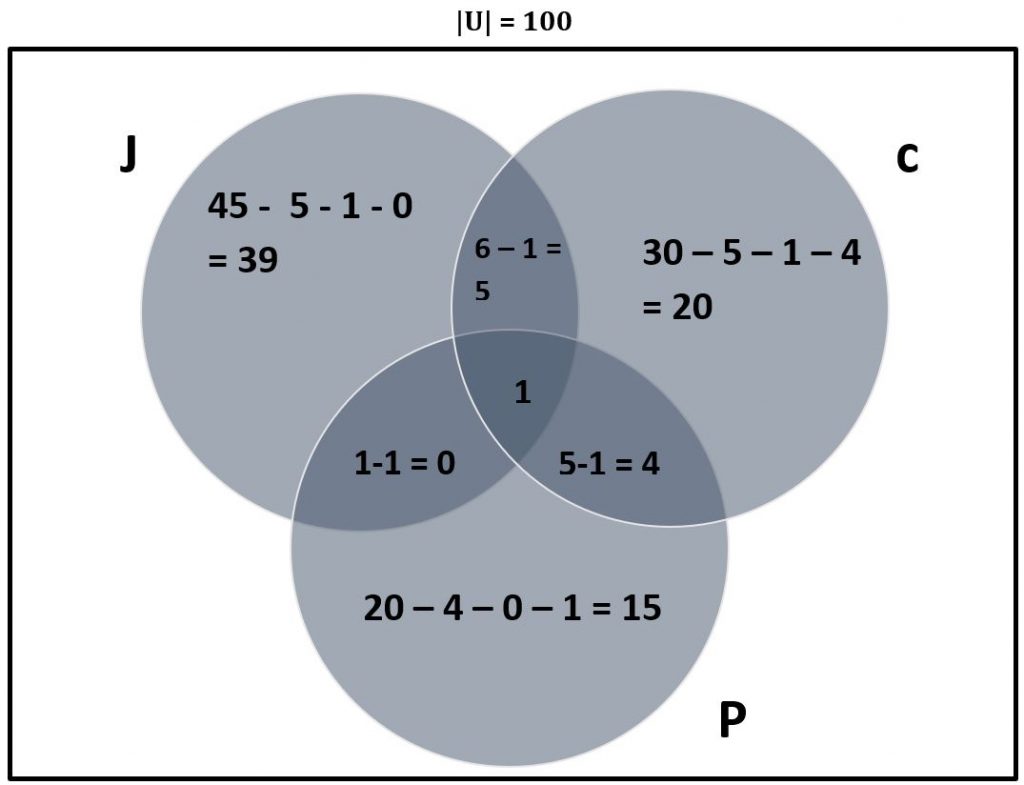
اکنون ممکن است از نمودار ون استفاده کنیم. این به سه دایره نیاز دارد زیرا سه مجموعه درگیر است. ابتدا با پر کردن تقاطع مرکزی هر سه دایره شروع کنید: J ∩ C ∩ P. سپس از تفریق برای تعیین کاردینالیته بخش های باقی مانده استفاده کنید.
اکنون اطلاعات کافی برای پاسخ به این سوال در اختیار داریم:
تعداد برنامه نویسان کامپیوتری که به هیچ یک از این سه زبان تسلط ندارند را مشخص کنید.
به عبارت دیگر، ما باید کاردینالیته متمم مجموعه J ∪ C ∪ P را تعیین کنیم. |J ∪ C ∪ P| را محاسبه کنید ابتدا قبل از تعیین مقدار مکمل:
|J ∪ C ∪ P|
= 39 + 5 + 20 + 4 + 15 + 1
= 84
حالا متمم را محاسبه کنید:
|(J ∪ C ∪ P)' | = |U| – |J ∪ C ∪ P|
= 100 - 84
= 16
16 برنامه نویس به هیچ یک از این سه زبان مهارت ندارند.
اصل گنجاندن-استخراج: مثال سه (سه مجموعه)
این مثال سوال اصل شمول-حذف را می توان به صورت جبری حل کرد.
سوال:
350 کشاورز در یک منطقه بزرگ وجود دارد. 260 عدد چغندر مزرعه، 100 عدد تربچه مزرعه، 70 عدد تربچه مزرعه، 40 عدد چغندر و تربچه مزرعه، 40 عدد سیب زمینی و تربچه و 30 عدد چغندر و سیب زمینی مزرعه. اجازه دهید B، Y، و R مجموعه مزارعی را نشان دهند که به ترتیب چغندر، یام و تربچه پرورش می دهند.
تعداد کشاورزانی که چغندر، یام و تربچه پرورش می دهند را تعیین کنید.
راه حل:
حروف برای نشان دادن مجموعه ها قبلاً در خود سؤال ارائه شده است (برخلاف مثال بالا). بنابراین، ما میتوانیم فوراً به اصلی بودن توجه کنیم:
|U| = 350
|B| = 260
|Y| = 100
|R| = 70
|B ∩ R| = 40
|Y ∩ R| = 40
|B ∩ Y| = 30
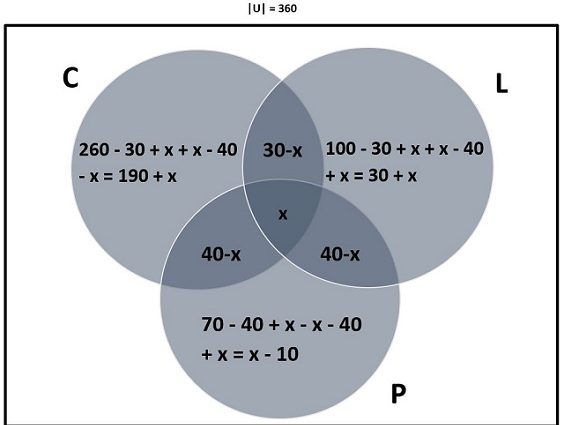
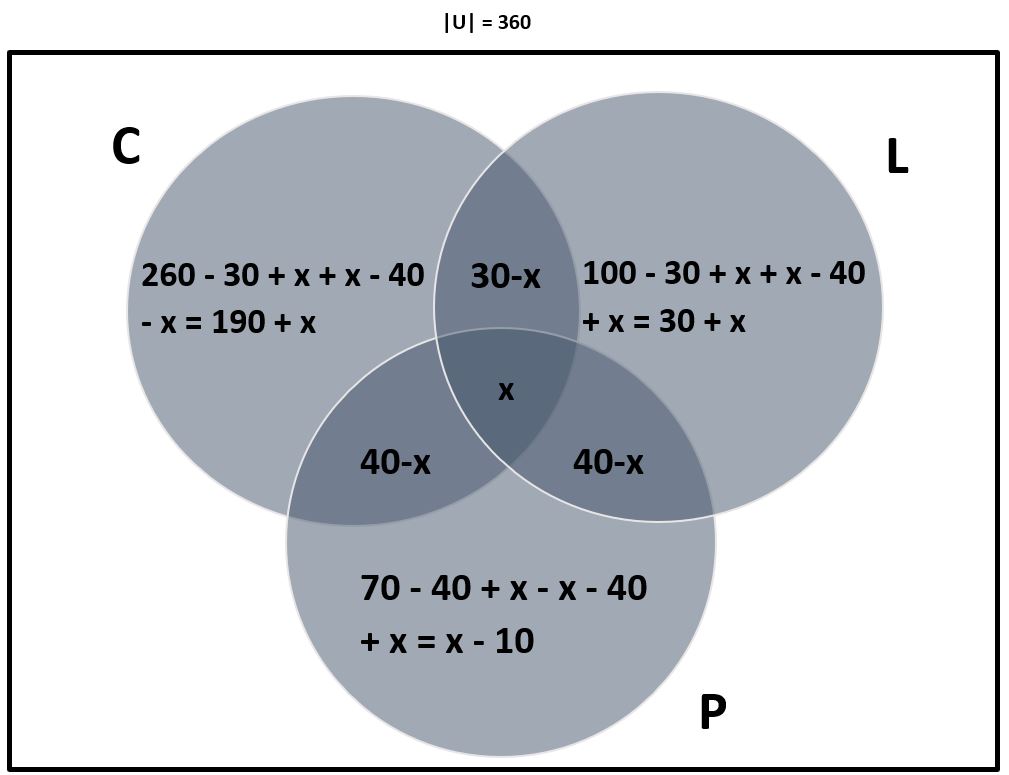
ما باید کاردینالیته تقاطع هر سه مجموعه را تعیین کنیم که |B ∩ Y ∩ R| است. این مجهولی است که می توانیم به صورت جبری تعیین کنیم. نمودار ون را با اطلاعات داده شده پر کنید. از x برای نشان دادن |B ∩ Y ∩ R| استفاده کنید .
اجازه دهید x کشاورزان چغندر، یام و تربچه پرورش دهند. یعنی اجازه دهید
|B ∩ Y ∩ R| = x
حالا x را به صورت جبری حل کنید:
|U|= 350 = 190 + x + (30 – x ) + x + (40 – x ) + (40 – x ) + 30 + x + x – 10
350 = 320 + x
x = 30
بنابراین 30 کشاورز چغندر، سیب زمینی و تربچه پرورش می دهند.
2018-11-21
بگذارید A مجموعه Painters
B باشد مجموعه Plumbers
C مجموعه برقکاران باشد.
داده شده،
|A| = 45
|B| = 50
|C| = 50
نامزد ماهر در هر سه حوزه
|A∩B∩C| = 15
همه آنها حداقل در یکی از این زمینه ها مهارت دارند. از این رو
|AUBUC| = 80
تعداد داوطلبانی که دقیقاً در 2 زمینه مهارت داشتند
= |A∩B| + |A∩C| + |B∩C|
با اصل گنجاندن – حذف،
|AUBUC| = |A| + |B| + |C|- [ |A∩B| + |A∩C| + |B∩C| ] + |A∩B∩C|
[ |A∩B| + |A∩C| + |B∩C| ] = |A| + |B| + |C| + |A∩B∩C| – |AUBUC|
= 45 + 50 + 50 + 15 - 80
= 80
لطفاً هر کسی این مشکل را حل کند،
در یک سایت ساخت و ساز، خورخه مسئول استخدام کارگران ماهر برای پروژه است. از 80 داوطلبی که با او مصاحبه کرد، متوجه شد که
45 نفر نقاش،
50 نفر برق،
50 نفر لوله کش،
15 نفر در هر سه زمینه مهارت داشتند و
همه آنها حداقل در یکی از این زمینه ها مهارت داشتند.
اگر همه کسانی را که دقیقاً در 2 زمینه مهارت داشتند را استخدام می کرد، چند نامزد استخدام می شد؟
 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.