دل نوشته ها ی نقش و آموزش ریاضی  

هدف این بخش مرجع نشان دادن نمودارهایی از انواع مختلف توابع است تا شما بتوانید با انواع آنها آشنا شوید. شما کشف خواهید کرد که هر نوع گراف دارای متمایز است. با نشان دادن چند نمودار در یک طرح، می توانید ویژگی های مشترک خود را ببینید. نمونه هایی از انواع توابع زیر در این گالری نمایش داده می شود:

• خطی
• درجه دوم
• قدرت
• چندجمله ای
• گویا
• نمایشی
• لگاریتمی
• سینوسی

در هر صورت استدلال (ورودی) تابع به نام x و مقدار (خروجی) تابع به نام y است . 
 

توابع خطی اینها توابع فرم هستند:

Y = متر X + ب ،

جایی که m و b ثابت هستند یک استفاده معمول برای توابع خطی تبدیل از یک مقدار یا مجموعه ای از واحدها به دیگری است. نمودارهای این توابعخطوط مستقیم هستند . متر شیب است و ب است Y رهگیری. اگر m مثبت باشد، خط به سمت راست بالا می رود و اگر m منفی باشد، خط به سمت راست می رود. توابع خطی در اینجا توضیح داده شده است . 
 

توابع درجه دوم اینها توابع فرم هستند:

Y = ایکس  2 + B X + C ،

جایی که a ، b و c ثابت هستند نمودارهای آنها پارابولاها نامیده می شوند . این بعد ساده ترین نوع عملکرد بعد از عملکرد خطی است. اشیاء سقوط در امتداد مسیرهای پارابولیکی حرکت می کنند. اگر a یک عدد مثبت باشد، پارابولا به سمت بالا باز می شود و اگر a یک عدد منفی باشد، پارابولا به پایین می رسد. توابع درجه دوم در اینجا توضیح داده شده اند . 
 

توابع قدرت اینها توابع فرم هستند:

Y = ایکس ب ، 

جایی که a و b ثابت هستند آنها نام خود را از این واقعیت که متغیر x به برخی از قدرت افزایش یافته است. بسیاری از قوانین فیزیکی (به عنوان مثال نیروی گرانشی به عنوان تابع فاصله بین دو اشیاء یا خمشی یک پرتو به عنوان تابع بار بر روی آن) در شکل عملکردهای قدرت هستند. فرض کنیم که a = 1 و در چند مورد برای b نگاه کنیم :

قدرت b یک عدد صحیح مثبت است. نمودار به سمت راست را ببینید وقتی x = 0 این توابع صفر هستند. وقتی x بزرگ و مثبت است، همه آنها بزرگ و مثبت هستند. هنگامی که X بزرگ و منفی است، آنهایی که حتی قدرت دارند بزرگ و مثبت هستند در حالی که کسانی که قدرت های عجیب و غریب دارند بزرگ و منفی هستند. 


قدرت b یک عدد صحیح منفی است. نمودار به سمت راست را ببینید هنگامی که x = 0 این توابع از تقسیم صفر رنج می برند، بنابراین همه بی نهایت هستند. هنگامی که x بزرگ و مثبت هستند، کوچک و مثبت هستند. وقتی xبزرگ و منفی است و آنهایی که حتی دارای قدرت هستند کوچک و مثبت هستند در حالی که کسانی که قدرت های عجیب و غریب دارند کوچک و منفی هستند. 


قدرت b تقریبی بین 0 و 1 است. گراف به سمت راست را ببینید. وقتی x = 0 این توابع صفر هستند. منحنی ها در اصل منشا عمودی است و به عنوان xافزایش می یابد اما منحنی به سمت محور x می رود. 


عملکرد قدرت در اینجا به طور کامل مورد بحث است . 
 

توابع چندجمله ای. اینها توابع فرم هستند:

y = a n  ·  x n + a n  -1  ·  x n  -1 + ... + a 2  ·  x  2 + a 1  ·  x + a 0 ،   

که در آن یک نفر ، N  -1 ، ...، 2 ، 1 ، 0 ثابت هستند. فقط توان تعداد مجاز x مجاز است. بالاترین قدرت X که رخ می دهد، درجه چند جمله ای نامیده می شود . این نمودار نمونه هایی از چندجمله های درجه 4 و درجه 5 را نشان می دهد. درجه می دهد حداکثر تعداد " ups & downs " که چند جمله ای می تواند داشته باشد و همچنین حداکثر تعداد عبور از محور x که می تواند داشته باشد.

چندجملهای برای ساخت منحنی صاف در برنامه های گرافیکی کامپیوتری و برای تقریب انواع دیگر توابع مفید هستند . چندجملهایها در اینجا شرح داده شده است . 
 

توابع منطقی این توابع نسبت دو چندجملهای است. یکی از زمینه های مطالعه که در آن مهم هستند، تحلیل ثبات سیستم های مکانیکی و الکتریکی است (که از تبدیل لاپلاس استفاده می کند). 

هنگامی که چند جمله ای در مخرج صفر است پس از آن تابع منطقی به عنوان توسط یک خط نقطه چین عمودی (به نام نشان داد بی نهایت می شود مجانب ) در نمودار آن است. به عنوان مثال به سمت راست این اتفاق می افتد زمانی که x = -2 و هنگامی که x = 7.

هنگامی که x بسیار بزرگ می شود، منحنی ممکن است خاموش شود. منحنی به سطوح مناسب در y = 5. 




گراف به سمت راست مثال دیگری از یک عملکرد منطقی را نشان می دهد. این یک تقسیم صفر درx = 0. این سطح را خاموش نمی کند، اما خط راست را y = x می گیرد وقتی x بزرگ است، همانطور که توسط خط نقطه نقطه (دیگری asymptote) نشان داده می شود. 
 

توابع نمایشی اینها توابع فرم هستند:

y = a b x ، 

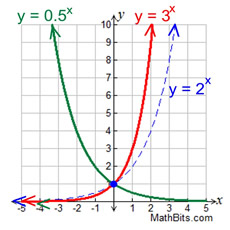
جایی که x در یک شاخص است (نه در پایه همانطور که در مورد توابع قدرت بود ) و a و b ثابت هستند. (توجه داشته باشید که تنها b به قدرت x ، نه a است .) اگر پایه b بزرگتر از 1 باشد، نتیجه رشد قیمتی است. بسیاری از مقادیر فیزیکی به طور نمادین رشد می کنند (به عنوان مثال جمعیت حیوانات و پول نقد در حساب سودمند). 



اگر پایه b کوچکتر از 1 باشد، نتیجه انحراف معکوس است. بسیاری از مقادیر به طور معکوس تجزیه می شوند (به عنوان مثال نور خورشید رسیدن به عمق داده شده از اقیانوس و سرعت یک شیء که به دلیل اصطکاک کاهش می یابد).


توابع نمایشی در اینجا توضیح داده شده است . 
 

توابع لگاریتمی روش های معادل بسیاری برای تعریف توابع لگاریتمی وجود دارد. ما آنها را به فرم تعریف می کنیم:

Y =  LN ( X ) +  ب ،

جایی که x در لگاریتم طبیعی است و a و b ثابت هستند. آنها فقط برای مثبت X تعریف می شوند . برای کوچک x آنها منفی هستند و برای بزرگ x آنها مثبت هستند اما کوچک می شوند. توابع لگاریتمی به درستی پاسخ پاسخ گوش انسان را به صداهای مختلف گسسته و پاسخ چشم انسان به نور درخشندگی متفاوت توصیف می کنند. توابع لگاریتمی در اینجا شرح داده شده اند . 
 

توابع سینوسی اینها توابع فرم هستند:

y = یک  گناه ( b x + c )،

جایی که a ، b و c ثابت هستند توابع سینوسی برای توصیف هر چیز که شکل موج را با توجه به موقعیت یا زمان مفید است مفید است. مثالها امواج بر روی آب، ارتفاع حوضه در طول روز و جریان متناوب در برق است. پارامتر a (دامنه نامیده می شود) بر ارتفاع موج تاثیر می گذارد، b (سرعت زاویه ای) بر عرض موج تاثیر می گذارد و c (زاویه فاز) موج را به سمت چپ یا راست حرکت می دهد. توابع سینوسی دراینجا توضیح داده شده اند .