|
چرخش یک تغییر و تحول که باعث چرخش یک رقم حدود یک نقطه ثابت به نام است مرکز چرخش . |
|
چرخش ها را می توان در شرایط مختلف مشاهده کرد:
زمین | آسیاب های بادی | چرخ دنده |
زمین هر 24 ساعت یکبار یک دور کامل در محور خود تجربه می کند. | تیغه های آسیاب های بادی انرژی باد را به انرژی چرخشی تبدیل می کنند. | یک اسباب بازی بچه گانه که هنگام دمیدن می چرخد. |
چرخش پارک تفریحی | چرخ و فلک | Merry-Go-Round |
پارکهای تفریحی ، مانند چرخش ، به شما امکان می دهد بخشی از یک چرخش شوید. | چرخ و فلک در اطراف یک مرکز مرکزی می چرخد. (بله ، صندلی ها برای جلوگیری از افتادن کج می شوند.) | در دور و بر ، سواران بخشی از چرخش در مورد مرکز سواری می شوند. |
چرخش های متمرکز بر مبدا:
| چرخش در صفحه مختصات خلاف جهت عقربه های ساعت است.
|
هنگام کار با چرخش ، باید بتوانید زاویه هایی با اندازه های خاص را تشخیص دهید. زوایای متداول شامل 30 درجه (یک سوم زاویه راست) ، 45 درجه (نصف زاویه راست) ، 90 درجه (زاویه راست) ، 180 درجه ، 270 درجه سانتیگراد و 360 درجه می باشد. همچنین باید جهت یک دایره واحد (دایره ای با شعاع 1 واحد) را درک کنید. توجه داشته باشید که حرکت درجه بر روی دایره واحد در خلاف جهت عقربه های ساعت حرکت می کند ، همان جهت شمارش چهارگوش ها: I ، II ، III ، IV. هنگام کار با چرخش روی یک شبکه مختصات ، این تصویر را در نظر داشته باشید. |  |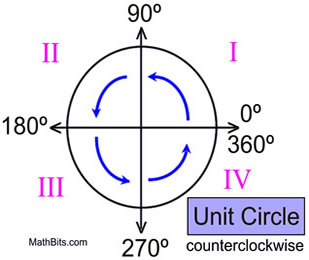
چرخش در صفحه مختصات: به
خاطر داشته باشید که چرخش در یک شبکه مختصات خلاف جهت عقربه های ساعت در نظر گرفته می شود ، مگر اینکه خلاف آن بیان شده باشد. در حالی که بیشتر چرخش ها در مبدأ متمرکز هستند ، مرکز چرخش در مسئله (یا در نماد) نشان داده می شود.
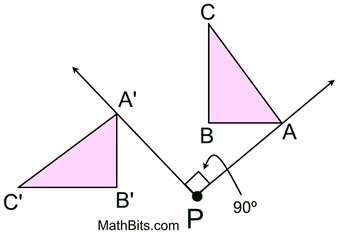
| با شروع با Δ ABC ، چرخش 90 درجه را در مرکز مبدا رسم کنید. (چرخش خلاف جهت عقربه های ساعت است.) برای اینکه "ببینید" این یک چرخش 90 درجه است ، نقطه B را که به پیکان قرمز متصل است تصور کنید . پیکان قرمز سپس 90 درجه جابجا می شود (توجه کنید که زاویه 90 درجه توسط دو پیکان قرمز شکل گرفته است). به موقعیت جدید نقطه B با برچسب B 'نگاه کنید . این رویکرد مشابه را می توان برای هر سه رأس استفاده کرد.
|
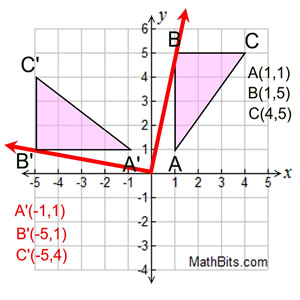
| با شروع با Δ ABC ، چرخش 180 درجه را در مرکز مبدا رسم کنید. (چرخش خلاف جهت عقربه های ساعت است.) همانطور که در مثال قبلی انجام دادیم ، تصور کنید که نقطه B از مرکز به پیکان قرمز متصل شده است (0/0). سپس پیکان 180 درجه (که یک خط مستقیم را تشکیل می دهد) منتقل می شود. به موقعیت جدید B با برچسب B 'توجه کنید.
|
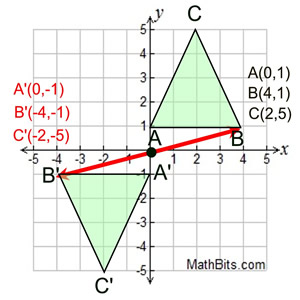
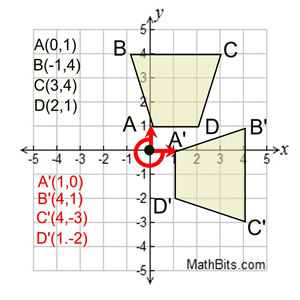
| با شروع چهار ضلعی ABCD ، چرخش 270 درجه سانتی گراد را در مبدأ رسم کنید. (چرخش خلاف جهت عقربه های ساعت است.) همانطور که در مثالهای قبلی انجام دادیم ، نقطه A را که از مرکز به پیکان قرمز متصل است تصور کنید (0/0). سپس پیکان 270 درجه (خلاف جهت عقربه های ساعت) منتقل می شود. به موقعیت جدید A با برچسب A 'توجه کنید. از آنجا که A "در" محور بود ، A 'نیز در محور است.
|
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.