دل نوشته ها ی نقش و آموزش ریاضی  

توجه داشته باشید

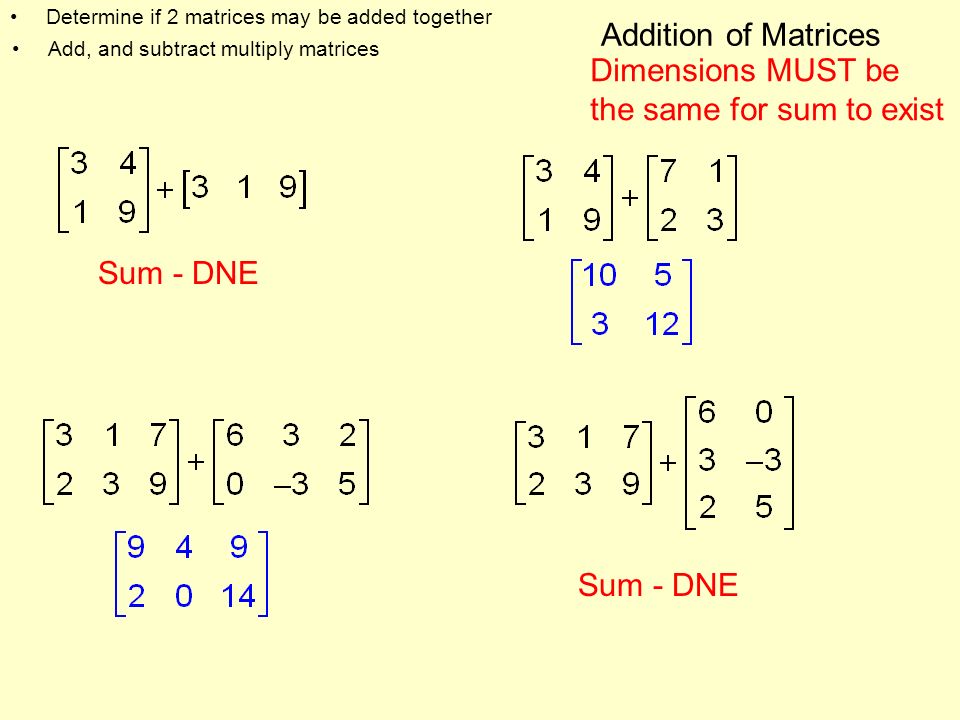
·اگر x و y دو عدد واقعی هستند به گونه ای که xy = 0 یا x = 0 یا y = 0 . اما این شرایط ممکن است با توجه به دو ماتریس صحیح نباشد.

·AB = 0 لزوماً دلالت بر این ندارد که A = 0 یا B = 0 یا هر دو A ، B = 0 باشد

تصویر

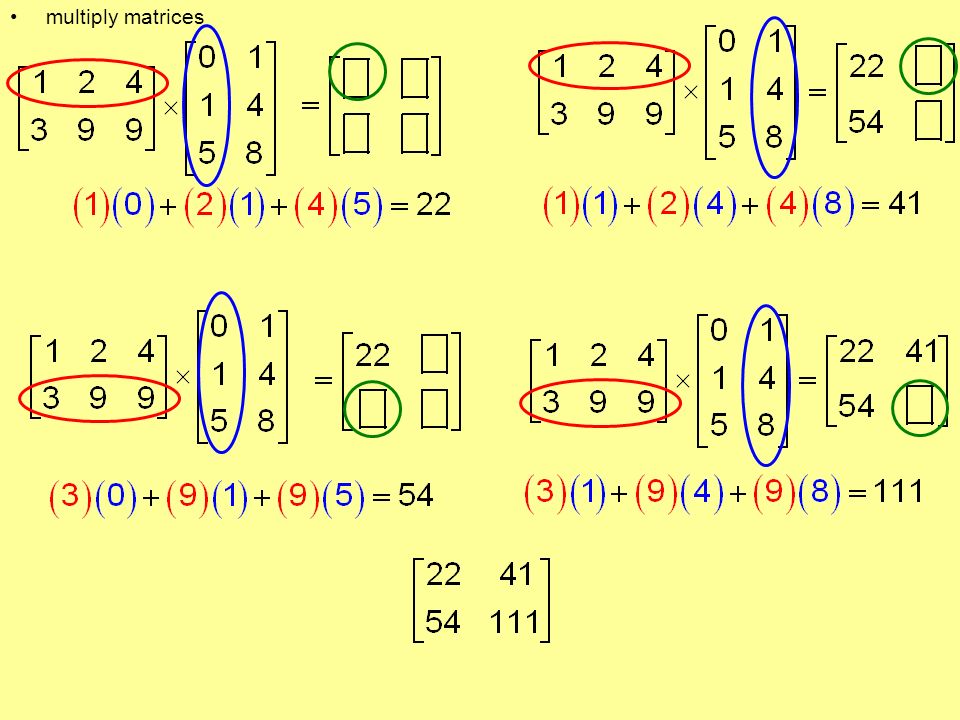
مثال 3.64

اگر  ، AB را پیدا کنید . 

راه حل

ما مشاهده می کنیم که A یک ماتریس 2 × 3 و B یک ماتریس 3 3 است ، از این رو AB تعریف شده است و از ترتیب 2 3 خواهد بود. 

مثال 3.65

اگر     بررسی کنید که آیا AB = BA است .

راه حل

مشاهده می کنیم که َAاست 2 × 2 و B است 2 × 2 ، از این رو AB تعریف شده است و آن را به مرتبه 2 × 2 باشد. 

بنابراین ، AB ≠ BA.

مثال 3.66

نشان دهید که A و B خاصیت تبادل نظر را با توجه به ضرب ماتریس برآورده می کند.

راه حل

ما باید نشان دهیم که AB = BA 

از این رو LHS = RHS (به عنوان مثال) AB = BA

مثال 3.67

با تعویض y = 2 در (1) ، 2 x + 2 = 4 x = 1 می دهد

بنابراین ، x = 1 ، y = 2.

مثال 3.68

نشان می دهد کهَA(BC)=(AB)C.

راه حل

A ( BC )   = (−1 - 4 + 14 3 - 3 - 2) = (9−2)… (2)

از (1) و (2) ، ( AB ) C = A ( قبل از میلاد ).

مثال 3.69

اگر   تأیید کنید که A ( B + C ) = AB + AC .

راه حل

مثال 3.70

اگر   نشان دهید که (AB) T = B T A T

راه حل

از (1) و (2) ، (AB)T = B T AT  .

1. مرتبه ماتریس ضرب AB  را پیدا کنید

2. اگر   Aاز مرتبه  P  × q  و  B از مرتبه  q× r  باشد  مرتبه  AB  و  BA چند است؟

3.  A است ' ، aردیف و a+ 3 ، ستون.  B  دارای سطرهای " b " و ستونهای " 17 - b"  است ، و اگر هر دو ضرب  AB  و  BA  وجود داشته باشند ، a ، b را پیدا کنید  ؟   

4- اگر      بررسی کنید   AB  =  BA ؟

5. با توجه به اینکه    تأیید کنید که  A ( B + C ) =  AB  +  AC .

6. نشان می دهد که ماتریس ها   ویژگی رفتاری AB = BA را برآورده می کنند 

1. P × R ، تعریف نشده است

2. 7،10

3. 3 × 3 ، 4 × 2 ، 4 × 2 ، 4 × 1 ، 1 3