۱۳۹۹/۰۳/۱۶ - - علی رضا نقش نیلچی -
1. بگذارید y = f ( x ) = x ^1/3 .
آ. یک گراف از F با استفاده از تکنولوژی های نموداری.
ب براساس نمودار ، f در هر دو حالت پیوسته و مشتق پذیر است ؟ ج براساس نمودار ، f کجاست اما فاقد مشتق پذیر است ؟
راه حل
آ.
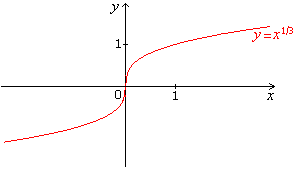
ب بر اساس نمودار ، f هم در همه جا پیوسته و مشتق پذیر است به جز در x = 0.
ج براساس نمودار ، f در حالت x = 0 مشتق پذیر ندارد .
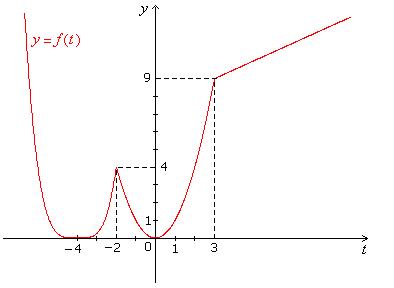
2. بگذارید f با
f ( x ) = | x 2 + 2 x - 3 |
تعریف شود . آ. نشان دهید که f در همه جا پیوسته است. ب با استفاده از تعریف مشتق نشان دهید که f در همه جا به جز x = - 3 و x = 1 مشتق پذیر است .
راه حل
آ. ما داریم | (f ( x ) = | ( x + 3 ) ( x - 1 . در جدول زیر علائم ( x + 3 ) ( x - 1 ) نشان داده شده است .
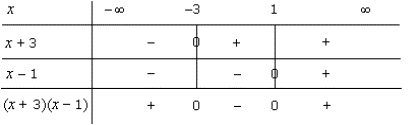
بنابراین ما:
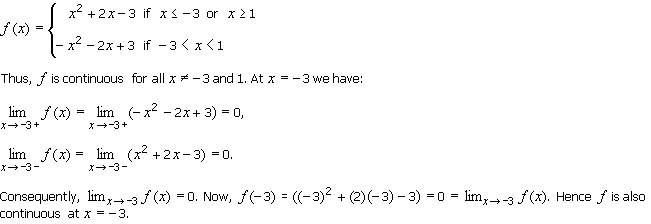
به طور مشابه ، f نیز در x = 1. پیوسته است. به این ترتیب که f در همه جا پیوسته است.
ب | 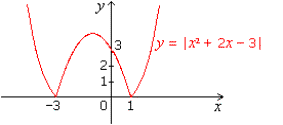
|
مورد که در آن x <- 3 یا x > 1. ما داریم:
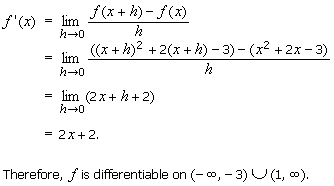
در مورد بازه (1و 3-). ما داریم:
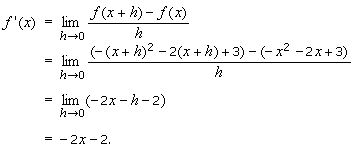
بنابراین f دربازه (1و 3-) مشتق پذیر است.
مورد که در آن x = - 3. ما داریم:
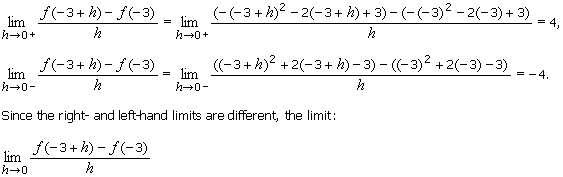
و بنابراین
f ' (- 3)
وجود ندارد. در نتیجه ، f در x = - 3 مشتق پذیرنیست.
مورد از کجا x = 1 . به طور مشابه ، f در x = 1 مشتق پذیر نیست.
به طور خلاصه ، f در همه جا به جز x = - 3 و x = 1 مشتق پذیر است.





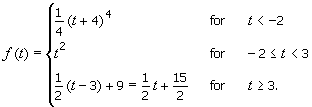


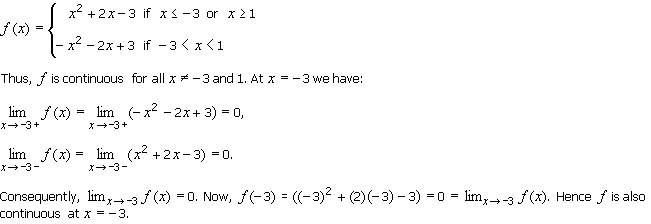

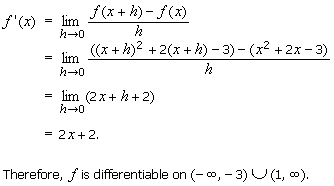
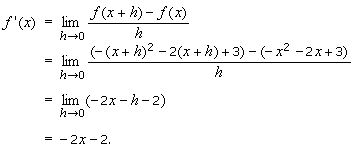
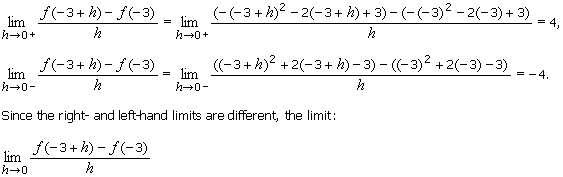






 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.