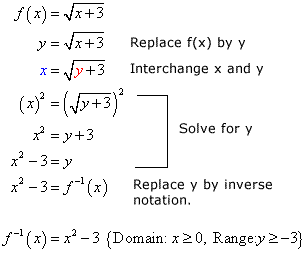دل نوشته ها ی نقش و آموزش ریاضی  

در ریاضیات اگر f تابعی از مجموعه A به مجموعه B باشد، آن گاه تابع وارون (معکوس) f یا f−1 تابعی از B به A است، با این ویژگی که برای هر x در دامنهٔ f، نتیجه‌ی اعمال پی‌درپی تابع و وارون آن روی x، خود x خواهد بود. به دیگر سخن:

تعریف

اگر R یک رابطه از مجموعه X به مجموعه Y باشد، آنگاه معکوس رابطه R را با R−1 نشان می‌دهیم که عبارت است از:

که رابطه‌ای از مجموعه Y به مجموعه X است. حال تابع f:X→Y نیز یک رابطه است. پس معکوس آن را نیز می‌توان تعریف کرد که آن را با f−1 نشان می‌دهیم و حداقل یک رابطه از Y به X است.

مثال اول (دو مجموعه)

سؤال:

از بین 50 بیمار بستری در بیمارستان ، 25 نفر مبتلا به ذات الریه ، 30 نفر برونشیت و 10 نفر با سینه پهلو و برونشیت هستند. تعیین کنید:

(الف) تعداد بیماران مبتلا به ذات الریه یا برونشیت (یا هر دو).

(ب) تعداد بیمارانی که به پنومونی یا برونشیت مبتلا نشده اند.

راه حل:

اولین قدم شناسایی رسمی مجموعه ها و مشخص کردن تعداد عناصر موجود در هر کدام است. این می تواند صرفاً با اطلاعات معین انجام شود. بدون محاسبه لازم است. با استفاده از این سوال اصلی ورود-خروج ، می توان سه مجموعه را به شرح زیر تعریف کرد:

بگذارید U تمام مجموعه بیماران را مشخص کند. بگذارید P و B مجموعه ای از بیماران مبتلا به پنومونی و برونشیت را به ترتیب نشان دهند. بدین ترتیب:

| U | = 50

| پ | = 25

| ب | = 30

| P  ∩ B | = 10

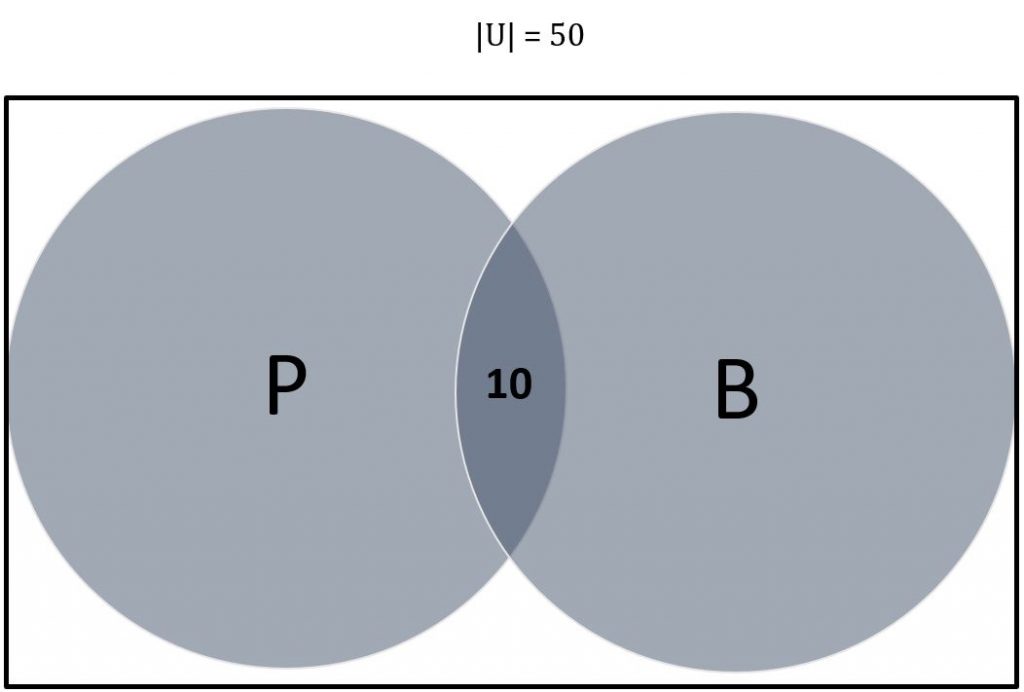
اکنون ممکن است یک نمودار Venn ایجاد کنیم. دو مجموعه وجود دارد و بنابراین دو دایره است. از آنجا که تعداد عناصر موجود در تقاطع P و B را می شناسیم (| P  ∩ B |) می توانیم این موارد را در ابتدا پر کنیم:

اکنون می توانیم محاسبه کنیم که چند عنصر فقط در P زندگی می کنند اما نه | P  ∩ B |:

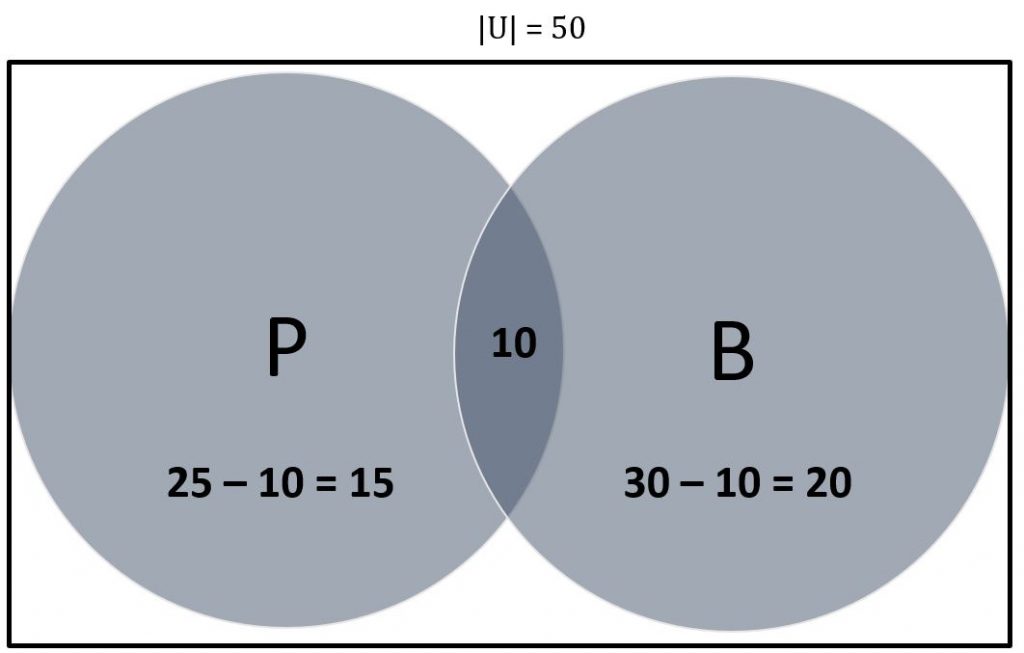
از آنجا که | پ | = 25 و | P  ∩ B | = 10 ، 15 (25-10 = 15) عنصر منحصر به فرد در P وجود دارد.

برای محاسبه تعداد عناصر تنها در B اما نه همان روش را دنبال کنید | P  ∩ B |:

از آنجا که | ب | = 30 و | P  ∩ B | = 10 ، 20 (30-10 = 20) عنصر منحصر به فرد در B وجود دارد.

این اطلاعات جدید باید به نمودار Venn ما به شرح زیر اضافه شود:

کار مقدماتی کامل است و ما اطلاعات کافی برای پاسخ مستقیم به سؤالات داریم:

(یک) تعیین تعداد بیماران مبتلا به ذات الریه یا برونشیت (یا هر دو).

این همان درخواست برای تعیین | P ∪ B | است. با نگاهی به نمودار Venn ، جواب را به صورت زیر تنظیم کنید:

| P ∪ B | = 15 + 10 + 20

= 45

بنابراین 45 بیمار مبتلا به پنومونی یا برونشیت تشخیص داده می شوند.

با استفاده از اصل شمول و خروج به طور مستقیم و بدون مراجعه به نمودار Venn ، می توانید به همین جواب برسید:

| P ∪ B | = | پ | + | ب | - | P ∪ B |

= (25 + 30) - (10)

= 45

بنابراین 45 بیمار مبتلا به پنومونی یا برونشیت تشخیص داده می شوند.

 (ب) تعداد بیمارانی که به پنومونی یا برونشیت مبتلا نشده اند را تعیین کنید.

این همان درخواست برای تعیین | (P ∪ B) '| است. ما می دانیم که در کل 50 بیمار وجود دارد - از این تعداد 45 بیمار مبتلا به ذات الریه یا برونشیت هستند. برای حل سوال از این استفاده کنید:

| U | = 50

| P ∪ B | = 45

از این رو،

| (P ∪ B) '|

= 50 - 45 = 5

5 بیمار به ذات الریه یا برونشیت مبتلا نمی شوند.