دل نوشته ها ی نقش و آموزش ریاضی  

معرفی

من فقط فکر کردم که یک تکنیک هوشمندانه را که زمانی برای یافتن مساحت چندضلعی های عمومی استفاده می کردم با شما به اشتراک بگذارم .

چند ضلعی می تواند منظم (همه زوایا مساوی و همه ضلع ها برابرند) یا نامنظم باشد

منظم	بی رویه

چند ضلعی مثال

بیایید از این چند ضلعی به عنوان مثال استفاده کنیم:

مختصات

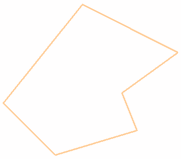
اولین مرحله این است که هر راس (گوشه) را به یک مختصات تبدیل کنید ، مانند نمودار:

بخش زیر یک خط

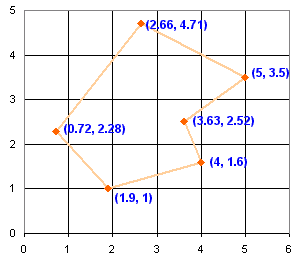
اکنون، برای هر پاره خط، ناحیه پایین تا محور x را مشخص کنید .

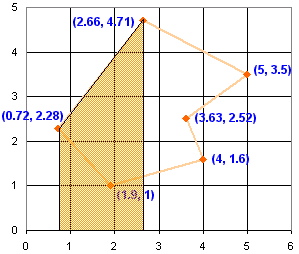
بنابراین، چگونه هر منطقه را محاسبه کنیم؟

میانگین دو ارتفاع را در نظر بگیرید، سپس در عرض ضرب کنید

مثال: برای شکل برجسته شده در بالا، دو ارتفاع (مختصات "y" 2.28 و 4.71) را می گیریم و ارتفاع متوسط ​​را محاسبه می کنیم:

(2.28+4.71)/2 = 3.495

عرض را محاسبه کنید (تفاوت بین مختصات "x" 2.66 و 0.72)

2.66-0.72 = 1.94

مساحت عرض×ارتفاع است:

1.94 × 3.495 = 6.7803

همه آنها را اضافه کنید

حالا همه آنها را جمع کنید!

اما ترفند این است که وقتی آنها به جلو می روند (عرض مثبت)، و وقتی به عقب می روند کم می کنیم (عرض منفی).

اگر همیشه در جهت عقربه های ساعت به دور چند ضلعی بروید و همیشه اولین مختصات "x" را از دومی کم کنید، به طور طبیعی انجام می شود، مانند این:

شما همچنین می توانید به سمت دیگر بروید. اگر یک ناحیه منفی دریافت کردید، آن را مثبت کنید.

و به نظر می رسد این است:

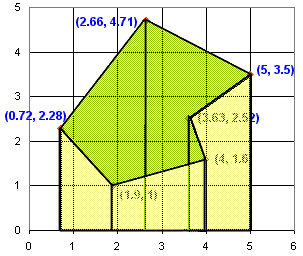
پس همین! مساحت 8.3593 است

​

محاسبه مساحت یک چند ضلعی می تواند به سادگی یافتن مساحت یک مثلث منتظم یا به پیچیدگی مساحت یک شکل یازده ضلعی نامنظم باشد. اگر می خواهید بدانید که چگونه مساحت چند ضلعی های مختلف را پیدا کنید، فقط این مراحل را دنبال کنید.

 مساحت یک ورق تقلب چند ضلعی نامنظم

قسمت1

مساحت چند ضلعی های منتظم را با استفاده از سهم های آنها بیابید

1. 

   1

   فرمول پیدا کردن مساحت چندضلعی منتظم را بنویسید. برای پیدا کردن مساحت یک چند ضلعی منتظم، تنها کاری که باید انجام دهید این است که این فرمول ساده را دنبال کنید: مساحت = 1/2 x محیط xسهم. [1] معنی آن این است:
   • محیط = مجموع طول همه اضلاع
   • سهم = پاره ای که مرکز چند ضلعی را به نقطه وسط هر ضلعی که بر آن ضلع عمود است می پیوندد [2]

2. 

   2

   سهم چندضلعی را پیدا کنید. اگر از روش سهم استفاده می کنید، سهم برای شما ارائه می شود. فرض کنید با یک شش ضلعی کار می کنید که یک سهم به طول 3√10 دارد.

3. 

   3

   محیط چند ضلعی را پیدا کنید. اگر محیط برای شما فراهم شده باشد، تقریباً کارتان تمام شده است، اما به احتمال زیاد کمی کار بیشتری برای انجام دادن دارید. اگر سهم برای شما ارائه شده است و می دانید که با یک چند ضلعی منظم کار می کنید، می توانید از آن برای پیدا کردن محیط استفاده کنید. در اینجا نحوه انجام آن آمده است:
   • فرض را به عنوان ضلع "x√3" یک مثلث 30-60-90 در نظر بگیرید. می توانید به این شکل فکر کنید زیرا شش ضلعی از شش مثلث متساوی الاضلاع تشکیل شده است. سهم یکی از آنها را به دو نیم می کند و مثلثی با زوایای 30-60-90 درجه ایجاد می کند.
   • می دانید که طرف مقابل زاویه 60 درجه دارای طول = x√3، ضلع روبروی زاویه 30 درجه دارای طول = x و ضلع روبروی زاویه 90 درجه دارای طول = 2x است. اگر 10√3 نشان دهنده "x√3" باشد، می توانید ببینید که x = 10.
   • می دانید که x = نصف طول ضلع پایین مثلث است. برای بدست آوردن طول کامل آن را دو برابر کنید. طول ضلع پایین مثلث 20 واحد است. شش ضلع از این شش ضلعی وجود دارد، بنابراین 20 در 6 را ضرب کنید تا 120، محیط شش ضلعی را بدست آورید.

4. 

   4

   سهم و محیط را به فرمول وصل کنید. اگر از ناحیه فرمول = 1/2 x محیط x سهم استفاده می کنید، می توانید 120 را برای محیط و 10√3 را برای سهم وصل کنید. در اینجا به نظر می رسد:
   • مساحت = 1/2 x 120 x 10√3
   • مساحت = 60*10√3
   • مساحت = 600√3

5. 

   5

   پاسخ خود را ساده کنید. ممکن است لازم باشد پاسخ خود را به جای جذر مربع به صورت اعشاری بیان کنید. فقط از ماشین حساب خود استفاده کنید تا نزدیکترین مقدار √3 را پیدا کنید و آن را در 600 ضرب کنید. √3 x 600 = 1,039.2. این پاسخ نهایی شماست.

قسمت2

یافتن مساحت چند ضلعی های منتظم با استفاده از فرمول های دیگر

1. 

   1

   مساحت یک مثلث منظم را پیدا کنید. اگر می‌خواهید مساحت یک مثلث منظم را پیدا کنید، تنها کاری که باید انجام دهید این است که این فرمول را دنبال کنید: مساحت = 1/2 x پایه x ارتفاع.
   • اگر مثلثی با پایه 10 و ارتفاع 8 دارید، مساحت = 1/2 x 8 x 10 یا 40 است.

2. 

   2

   مساحت مربع را پیدا کنید. برای پیدا کردن مساحت مربع کافیست طول یک ضلع آن را مربع کنید. این در واقع همان چیزی است که پایه مربع را در ارتفاع آن ضرب کنیم، زیرا پایه و ارتفاع یکسان هستند.
   • اگر طول ضلع مربع 6 باشد، مساحت آن 6×6 یا 36 است.

3. 

   3

   مساحت یک مستطیل را پیدا کنید . برای پیدا کردن مساحت یک مستطیل، کافی است پایه را در ارتفاع ضرب کنید.
   • اگر قاعده مستطیل 4 و ارتفاع آن 3 باشد، مساحت مستطیل 4×3 یا 12 است.

4. 

   4

   مساحت ذوزنقه را پیدا کنید. برای پیدا کردن مساحت ذوزنقه، فقط باید این فرمول را دنبال کنید: مساحت = [(پایه 1 + پایه 2) x ارتفاع]/2.
   • فرض کنید شما یک ذوزنقه با پایه هایی دارید که طول آن 6 و 8 و ارتفاع آن 10 است. مساحت آن ساده است [(6 + 8) x 10]/2، که می توان آن را به (14 x 10)/2 ساده کرد. ، یا 140/2 که مساحت 70 را می سازد.

قسمت3

پیدا کردن مساحت چند ضلعی های نامنظم

1. 

   1

   مختصات رئوس [3] چندضلعی نامنظم را بنویسید . تعیین مساحت یک چندضلعی نامنظم را زمانی می توان پیدا کرد که مختصات رئوس را بدانید. [4]

2. 

   2

   یک آرایه ایجاد کنید. مختصات x و y هر رأس چند ضلعی را به ترتیب خلاف جهت عقربه های ساعت فهرست کنید. مختصات اولین نقطه در انتهای لیست را تکرار کنید.

3. 

   3

   مختصات x هر راس را در مختصات y راس بعدی ضرب کنید. نتایج را اضافه کنید. جمع اضافه این محصولات 82 می باشد.

4. 

   4

   مختصات y هر راس را در مختصات x راس بعدی ضرب کنید. باز هم این نتایج را اضافه کنید. مجموع اضافه شده این محصولات -38 است.

5. 

   5

   مجموع حاصلضرب های دوم را از مجموع مصنوعات اول کم کنید. 38- را از 82 کم کنید تا 82 - (38-) = 120 به دست آید.

6. 

   6

   این اختلاف را بر 2 تقسیم کنید تا مساحت چندضلعی را بدست آورید. فقط 120 را بر 2 تقسیم کنید تا به 60 برسید و همه چیز تمام است.