دل نوشته ها ی نقش و آموزش ریاضی  

بر اساس زوایای داخلی، همه چند ضلعی ها به طور کلی به دو گروه محدب و مقعر تقسیم می شوند.

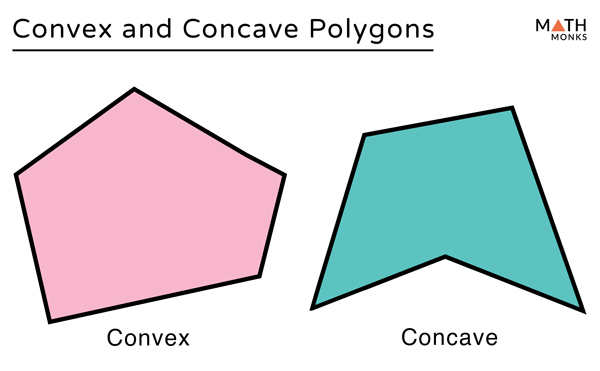
چند ضلعی های محدب در مقابل مقعر

چند ضلعی محدب چیست؟

چند ضلعی محدب چند ضلعی است که تمام زوایای داخلی آن کمتر از 180 درجه باشد. تمام قطرهای یک چند ضلعی محدب در داخل شکل بسته قرار دارند. یک چند ضلعی محدب می تواند هم منظم و هم نامنظم باشد. چند ضلعی های محدب منتظم همه اضلاع با طول یکسان و تمام زوایای داخلی با اندازه یکسان (کمتر از 180 درجه) دارند. به چند ضلعی های محدب که منظم نیستند، چند ضلعی های محدب نامنظم می گویند.

مثال ها : مثلث ها، همه چهارضلعی های محدب، پنج ضلعی منتظم و شش ضلعی منتظم همگی چند ضلعی محدب هستند. مربع یک چندضلعی محدب منظم است.

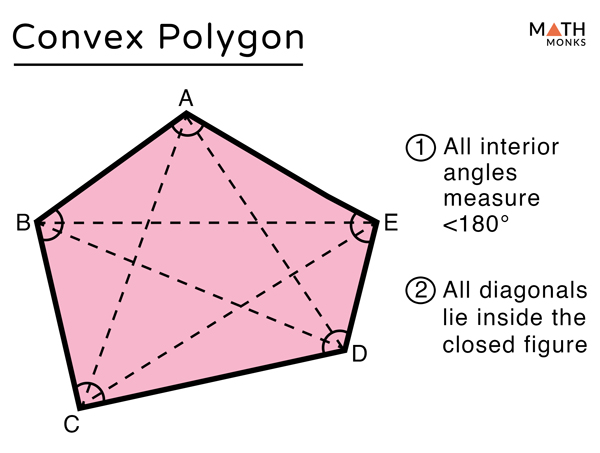
چند ضلعی محدب

خواص

1. همه زوایای داخلی کمتر از 180 درجه هستند. اندازه گیری ∠ABC، ∠BCD، ∠CDE، ∠DEF، ∠EFA و ∠FAB کمتر از 180 درجه
2. تمام 9 قطر در داخل شکل بسته قرار دارند. قطرهای AC، AD، AE، BD، BE، BF، CE، CF و CA در داخل شکل قرار دارند.
3. مجموع تمام زوایای بیرونی 360 درجه است
4. مجموع تمام زوایای داخلی دارای n ضلع با ( n – 2) x 180 درجه داده می شود.

در پنج ضلعی داده شده ABCDE همه زوایای داخلی از اندازه مساوی هستند. بیان کنید که چند ضلعی محدب است یا خیر.

راه حل:

همانطور که می دانیم،
زاویه داخلی یک چند ضلعی منظم = (N-2) × 180 درجه / N، در اینجا و 5 = n
= (5/2) × 180 درجه / 5
= 3 * 180 ° / 5
= 108 درجه سانتی
از آنجا که همه پنج زاویه داخلی در پنج ضلعی داده شده کمتر از 180 درجه است، این یک چند ضلعی محدب است.

فرمول ها

حوزه

این فضای کل محصور در چند ضلعی است. فرمول زیر آورده شده است:

مساحت ( A ) = ½|(x 1 y 2 – x 2 y 1 )+(x 2 y 3 – x 3 y 2 )+……..+(x n y 1 – x 1 y n )|، اینجا (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3 ),…….., (x n , y n ) رئوس چند ضلعی در صفحه مختصات هستند

مساحت چند ضلعی محدب را با رئوس (5، 2) (12، 8) و (5، -2) بیابید.

راه حل:

همانطور که می دانیم،
مساحت (A) = ½|(x 1 y 2 – x 2 y 1 )+(x 2 y 3 – x 3 y 2 )+(x 3 y 1 – x 1 y 3 )|،
در اینجا ( x 1 , y 1 ) = (5, 2), (x 2 , y 2 ) = (12, 8), (x 3 , y 3 ) = (5, -2)
 = ½|(40-24)+ (-24-40)+ (10)-10)|
= ½|16-64|
= 48/2

زوایای داخلی

زوایای داخلی یک چند ضلعی زوایایی هستند که در داخل چند ضلعی یافت می شوند. یک چند ضلعی به اندازه تعداد اضلاع دارای زوایای داخلی است.

مجموع زوایای داخلی

این اندازه گیری کل تمام زوایای داخلی ترکیب شده در چند ضلعی است. فرمول تعیین مجموع تمام زوایا در هر چندضلعی منتظم محدب در زیر آمده است:

مجموع اندازه زوایای داخلی = ( n -2) × 180 درجه، در اینجا n = تعداد کل اضلاع چند ضلعی

مجموع زوایای داخلی را در یک چندضلعی منتظم محدب 14 ضلعی محاسبه کنید.

راه حل:

همانطور که می دانیم،
مجموع اندازه زوایای داخلی = (n-2) × 180 درجه، در اینجا n = 22
 = (14-2) x 180 درجه
= 2160 درجه

یک زاویه داخلی

هر زاویه داخلی در یک چند ضلعی محدب منظم یکسان است و می توان با تقسیم مجموع زوایای داخلی بر تعداد کل اضلاع به دست آورد. فرمول زیر آورده شده است:

زاویه داخلی یک چند ضلعی محدب = ( n -2) × 180 درجه / n ، در اینجا n = تعداد کل اضلاع چند ضلعی

اندازه زوایای داخلی یک چند ضلعی منتظم محدب با 12 ضلع را بیابید.

راه حل:

همانطور که می دانیم،
زاویه داخلی یک چند ضلعی منتظم = (n-2) × 180 ° /n، در اینجا n = 18
 = (18-2) x 180 ° / 18
= 16 x 180 ° / 18
= 160 °

زوایای بیرونی

زاویه بیرونی یک چند ضلعی، زاویه ای است که از یک ضلع و امتداد ضلع مجاور تشکیل می شود.

قضیه مجموع زاویه خارجی بیان می کند که مجموع زوایای بیرونی هر چند ضلعی محدب 360 درجه است. برای چند ضلعی های محدب منظم با n ضلع، هر زاویه خارجی با استفاده از فرمول زیر تعیین می شود:

زاویه بیرونی یک چند ضلعی منتظم محدب = 360 درجه / n ، در اینجا n = تعداد کل اضلاع چند ضلعی

زاویه بیرونی را در یک چند ضلعی محدب منظم 15 وجهی محاسبه کنید.

راه حل:

 همانطور که می دانیم،
زاویه بیرونی یک چند ضلعی منتظم = 360 درجه / n، در اینجا n = 15
 = 360 درجه / 15
= 24 درجه

چند ضلعی مقعر چیست؟

یک چند ضلعی مقعر که به عنوان چند ضلعی غیر محدب نیز شناخته می شود، حداقل یکی از زوایای داخلی آن بیش از 180 درجه است. برخی از قطر های یک چند ضلعی مقعر خارج از شکل بسته قرار دارند.

همه چند ضلعی های مقعر نامنظم هستند زیرا تمام زوایای داخلی دارای اندازه های متفاوتی هستند. بنابراین چند ضلعی های مقعر هرگز منظم نیستند.

مثال ها : یک دارت یا یک نوک پیکان در چهار ضلعی، مقداری پنج ضلعی نامنظم و شش ضلعی

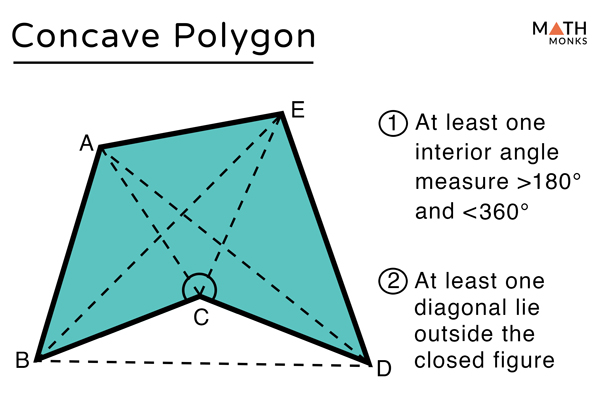
چند ضلعی مقعر

خواص

1. حداقل یک زاویه بازتابی بیشتر از 180 درجه و کمتر از 360 درجه دارد. ∠DEF بیشتر از 180 درجه و کمتر از 360 درجه است
2. حداقل یک راس به سمت داخل دارد. نقطه راس C به سمت داخل
3. دارای یک یا چند قطر است که خارج از شکل بسته قرار دارند. DF قطر خارج از شکل بسته قرار دارد
4. اگر پاره خطی با عبور از چندضلعی مقعر رسم شود، بیش از دو بار مرز را قطع خواهد کرد.

مجموع زوایای داخلی شش ضلعی ABCDEF داده شده 720 درجه است. اگر ∠ABC = 78 درجه، ∠BCD = 140 درجه، ∠CDE = 80 درجه، ∠EFA = 88 درجه، ∠FAB = 130 درجه. ∠DEF را پیدا کنید و بگویید آیا چند ضلعی ABCDEF مقعر است یا خیر.

راه حل:

همانطور که می دانیم،
مجموع زوایای شش ضلعی ABCDEF = 720°
بنابراین، ∠ABC + ∠BCD + ∠CDE +∠DEF + ∠EFA + ∠FAB =
78° + 140° + 80° +∠DEF + 88° + 130° = 720°
=> ∠DEF = 720° – 516°
=> ∠DEF = 204°
از آنجایی که ∠DEF بزرگتر از 180 درجه است، چند ضلعی ABCDEF یک چند ضلعی مقعر است. همچنین اگر خطی را رسم کنیم که نقاط D و F را به هم متصل می کند، متوجه می شویم که DF قطر خارج از شکل بسته قرار دارد، که بیشتر ثابت می کند که ABCDEF یک چند ضلعی مقعر است.

فرمول ها

حوزه

از آنجایی که تمام اضلاع و زوایای داخلی یک چند ضلعی مقعر برابر نیستند، هیچ فرمول استانداردی برای تعیین مساحت آنها وجود ندارد. برای تعیین مساحت یک چند ضلعی مقعر، باید چند ضلعی را به اشکالی مانند مثلث، مستطیل، متوازی الاضلاع یا اشکال دیگر تقسیم کرده، مساحت هر یک از این اشکال را پیدا کرده و در نهایت آنها را با هم جمع کنیم تا مساحت کل چند ضلعی به دست آید. بنابراین مساحت یک چندضلعی مقعر برابر است با:

مساحت ( A ) = مجموع مساحت تمام اشکال موجود در چند ضلعی

محیط

کل فاصله ای است که در اطراف مرز چند ضلعی طی می شود. محیط یک چند ضلعی مقعر به سادگی با جمع کردن طول همه ضلع ها به دست می آید. بنابراین محیط عبارت است از:

محیط ( P ) = مجموع تمام اضلاع چند ضلعی

بیایید این مفاهیم را با استفاده از مثال ها درک کنیم.

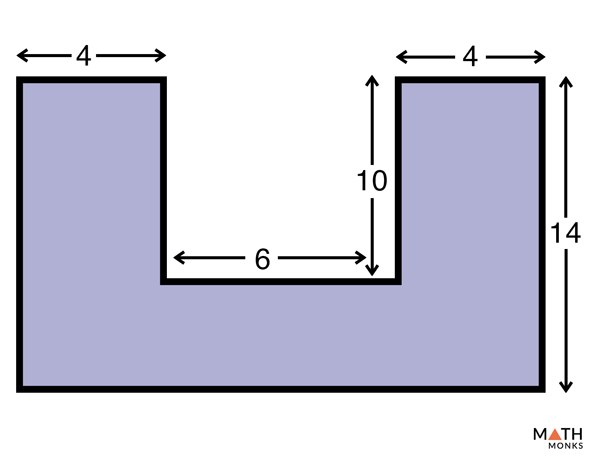مساحت و محیط چندضلعی مقعر را با اندازه های ضلع داده شده بیابید.

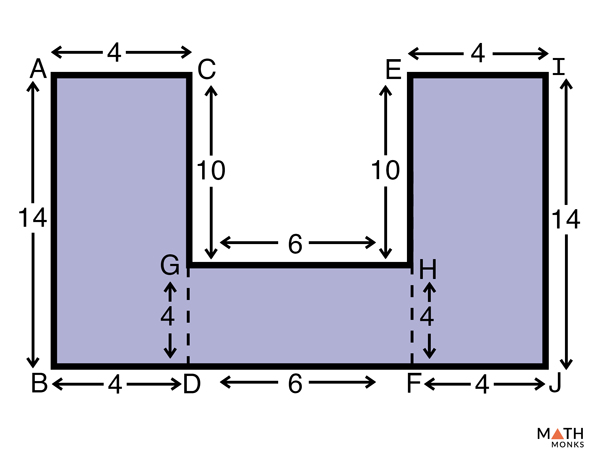
راه حل:

چند ضلعی داده شده به سه مستطیل تقسیم می شود. با یافتن مساحت هر مستطیل و جمع آنها مساحت چندضلعی بدست می آید.
بنابراین، مساحت چند ضلعی = مساحت مستطیل ABCD + مساحت مستطیل GDHF + مساحت مستطیل EFIJ
= (14 x 4) + (6 x 4) + (14 x 4)
= 56 + 24 + 56
= 136 واحد مربع
محیط از چند ضلعی = AB + BD + DF + FJ + IJ + EI + EH + GH + CG + AC
= (14 + 4 + 6 + 4 + 14 + 4 + 10 + 6 + 10 + 4)
= 76 واحد

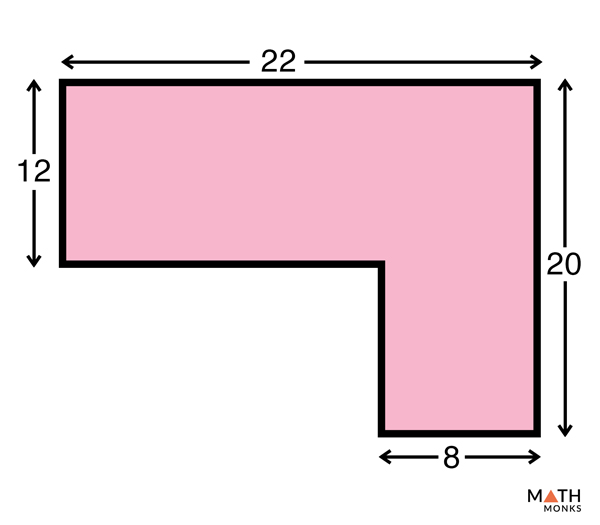تمام اضلاع چند ضلعی مقعر داده شده را پیدا کنید. سپس مساحت و محیط آن را پیدا کنید. (ترفند: چند ضلعی نامنظم داده شده را به دو چند ضلعی منتظم تقسیم کنید)

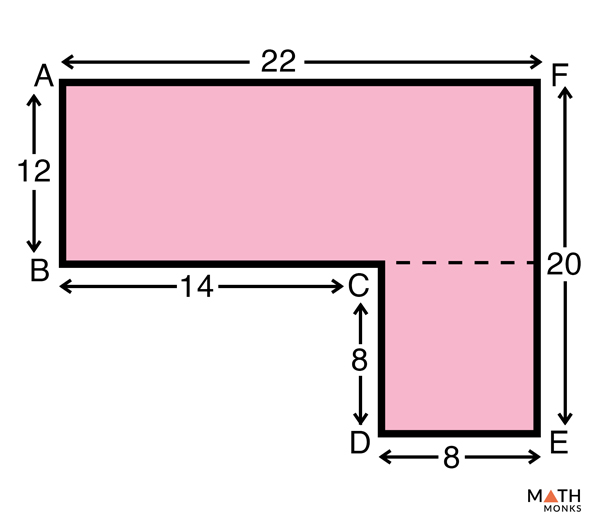
راه حل:

چند ضلعی داده شده به یک مستطیل و یک مربع تقسیم می شود. با یافتن مساحت مستطیل و مربع و جمع آنها مساحت چندضلعی بدست می آید.
بنابراین، مساحت چند ضلعی = مساحت مستطیل ABGF + مساحت مربع CDEG
= (22 x 12) + (8 x 8)
= 264 + 64
= 328 واحد مربع
محیط چند ضلعی = AB + BC + CD + DE + FE + AF
= (12 + 14 + 8 + 8 + 20 + 22)
= 84 واحد

زوایای داخلی

برای تعیین مجموع زوایای داخلی از فرمول زیر استفاده می کنیم:

مجموع زوایای داخلی = ( n -2) × 180 درجه، در اینجا n = تعداد کل اضلاع چند ضلعی

زوایای بیرونی

مثل همه چند ضلعی های دیگر، قضیه مجموع زاویه بیرونی که بیان می کند مجموع زوایای بیرونی تا 360 درجه است، برای همه چند ضلعی های مقعر صادق است.

سوالات متداول

Q1. چند ضلعی محدب چند ضلع دارد؟

جواب . یک چند ضلعی باید حداقل سه ضلع داشته باشد و می تواند حداکثر تعداد ضلع داشته باشد.

Q2. چرا یک مثلث متساوی الاضلاع یک چند ضلعی محدب منظم است؟

جواب . یک مثلث متساوی الاضلاع دارای هر سه ضلع با طول و تمام زوایای با اندازه مساوی است. از آنجایی که مجموع زوایای یک مثلث 180 درجه است، هر یک از زاویه ها 60 درجه است. بنابراین یک مثلث متساوی الاضلاع همیشه یک چندضلعی محدب منظم است.

Q3. پاره خطی که دو راس غیر متوالی یک چند ضلعی محدب را به هم می پیوندد را نام ببرید؟

جواب . قطر پاره خطی است که دو راس غیر متوالی یک چند ضلعی محدب را به هم می پیوندد