دل نوشته ها ی نقش و آموزش ریاضی  

شرایط کلیدی

o چند وجهی

o وجه

o یال

o منشور

o منشور راست

اهداف

o چندوجهی و منشور را بشناسید و قادر به تجزیه و تحلیل مثال های ساده از این اشکال باشد

o نحوه استفاده از فرمول های حجم و مساحت کره ها و استوانه ها را بدانید

ابتدا حجم و مساحت چند شکل سه بعدی ساده را در نظر می گیریم سپس به اشکال ترکیبی سه بعدی می پردازیم.

حجم و مساحت سطح

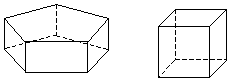
ما دو نوع اساسی از جامدات هندسی را در نظر خواهیم گرفت: چند وجهی و کره. یک چند وجهی اساساً یک شکل جامد n ضلعی است - این آنالوگ سه بعدی یک چند ضلعی است. چند نمونه از چند وجهی در زیر نشان داده شده است.

چندوجهی ها با وجه هایشان که نواحی چندضلعی هستند، یال ها، که پاره های خطی هستند که وجه ها و در نتیجه چند وجهی را مشخص می کنند، و رئوس که به همان شکلی که برای چندضلعی ها تعریف می شوند، تعریف می شوند. یک نوع خاص از چند وجهی یک منشور است که یک چندوجهی با بالا و پایین یکسان (و موازی) است. اگر اضلاع منشور در زوایای قائم به بالا و پایین برخورد کنند، آن را منشور راست می نامند. دو چند وجهی در سمت چپ ردیف مثال‌های بالا منشور هستند - ما می‌توانیم این موضوع را با استفاده از خطوط شکسته برای نشان دادن بخش‌هایی که خارج از دید هستند، با دقت بیشتری ببینیم.

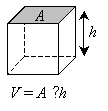
باز هم توجه کنید که وجهه های بالا و پایین (پایه ها) یکسان هستند. علاوه بر این، اینها در واقع منشورهای راست هستند (با فرض اینکه زوایای تشکیل شده بین اضلاع و پایه ها درست باشند، همانطور که در نمودارها به نظر می رسد). واضح است که حجم V یک منشور راست به سادگی مساحت A قاعده ضربدر ارتفاع h اضلاع است، همانطور که برای مکعب (یک منشور شش وجهی) در زیر نشان داده شده است.

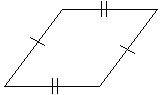
اما اگر منشور منشور درست نباشد چه؟ همین فرمول صدق می کند. بیایید با استفاده از منشور شش وجهی نگاهی به چرایی این موضوع بیندازیم. ما به این شکل "در انتهای" نگاه خواهیم کرد به طوری که عمق آن عمود بر سطح صفحه باشد (به عبارت دیگر، دو پایه قابل مشاهده نیستند). از تعریف منشور می دانیم که پاره های خط مقابل (یال ها) همخوان هستند.

حالا بیایید جامد را مطابق شکل زیر تقسیم کنیم و دو جامد مثلثی و یک جامد مستطیلی تشکیل دهیم. توجه داشته باشید که خط چین هم ارتفاع منشور است.

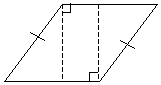
از خواص مستطیل ها موارد زیر را می دانیم.

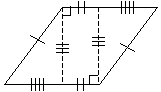
با شرط SSS، بنابراین می دانیم که دو مثلث متجانس هستند. بیایید شکل را به وجه زیر برچسب گذاری کنیم، توجه داشته باشیم که پایه b شکل برابر با b 1 + b 2 است.

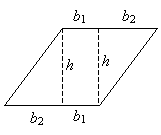
اکنون می توانیم مساحت این وجه از شکل را محاسبه کنیم.

اما مساحت پایه ها بین نسخه های راست و غیر راست منشور بدون تغییر است. به عبارت دیگر، عمق در این حالت و در مورد منشور راست (اگر به یک شکل جهت گیری شود) یکسان است. در نتیجه، حجم نیز یکسان است. اگرچه ما این واقعیت را فقط برای منشورهای شش وجهی نشان داده‌ایم، این امر در مورد همه منشورها صدق می‌کند: حجم، مساحت پایه ضرب در ارتفاع است.

مسئله تمرین : حجم منشور زیر را محاسبه کنید.

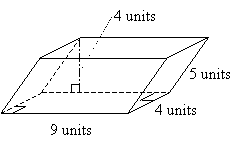
راه حل : چند وجهی در نمودار به عنوان یک منشور شناخته می شود. بر اساس زوایای قائمه در پایه (و در نتیجه هر دو پایه) می توان پایه ها را مستطیل هایی با طول 4 واحد و عرض 9 واحد تشخیص داد. بنابراین مساحت قاعده منشور 36 واحد مربع است. ارتفاع منشور در نمودار 4 واحد نشان داده شده است. بنابراین می توانیم حجم V منشور را به وجه زیر محاسبه کنیم.

V = bh = (36 واحد 2 ) (4 واحد) = 144 واحد 3

محاسبه حجم چند وجهی عمومی ممکن است دشوار باشد، بنابراین ما آنها را در عمق بیشتری در نظر نخواهیم گرفت. فرمول‌ها در کتاب‌ها و در اینترنت در دسترس هستند، اما برای چندوجهی خاص.

پارامتر دیگری که می توانیم محاسبه کنیم مساحت شکل است. صرف نظر از چند وجهی، مساحت سطح به سادگی مجموع مساحت تمام وجوه شکل است. به عنوان مثال، در مورد یک مکعب (منشور شش وجهی)، مساحت سطح به سادگی شش برابر مساحت هر وجهی است (همه وجه ها مساحت یکسانی دارند، زیرا همه یال ها همخوان هستند). (یا اگر طول هر یال s باشد، مساحت سطح آن 6 s 2 است.)

مسئله تمرین : مساحت سطح منشور را از مسئله تمرینی قبل محاسبه کنید، با این فرض که شکل فقط به سمت راست مایل است.

راه حل : یک بار دیگر به نمودار منشور در اولین مسئله تمرین نگاه کنید. با محاسبه مساحت هر وجه می توانیم مساحت سطح را پیدا کنیم. قبلاً می دانیم که پایه ها هر کدام 36 واحد مربع مساحت دارند. که چهار طرف ناشناخته را ترک می کند. مشکل به ما می گوید که شکل فقط به سمت راست مایل است (در نمودار زیر با قوس نشان داده شده است) - بنابراین، تنها زوایای غیر راست در وجه جلو و عقب هستند. این دو وجه متوازی الاضلاع هستند. وجه چپ و راست مستطیل هستند.

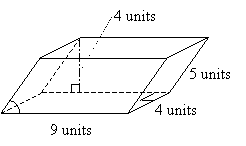
وجه چپ و راست هر دو دارای مساحتی هستند که حاصل ضرب 4 واحد و 5 واحد یا 20 واحد مربع است. وجه های جلو و عقب متوازی الاضلاع با پایه های 9 واحد و ارتفاع 4 واحد هستند، بنابراین مساحت هر کدام 36 واحد مربع است. بیایید اکنون کل سطح، S را پیدا کنیم .

S = (36 + 36) + (20 + 20) + (36 + 36) = 184 واحد 3

کره ها نوع دیگری از شکل های سه بعدی هستند که حجم و مساحت سطح آن ها به راحتی قابل محاسبه است. یک کره آنالوگ سه بعدی یک دایره است - با یک نقطه مرکزی O و یک شعاع r تعریف می شود. کره مجموعه تمام نقاطی است که در فاصله r از O قرار دارند. نمونه ای از یک کره در زیر نشان داده شده است.

مانند دایره ها، استخراج فرمول ها از نظر هندسی دشوار است، اما فرمول ها به خوبی شناخته شده اند. حجم V و سطح S برای کره ای به شعاع r در زیر آورده شده است .

شکل مشابه، استوانه (دایره ای) است که دارای دو پایه دایره ای متجانس و بدنه ای لوله ای شکل است، همانطور که در زیر نشان داده شده است. یک استوانه با شعاع r پایه های آن و ارتفاع آن h تعریف می شود.

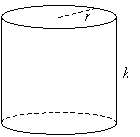
مانند منشور، حجم V استوانه حاصل ضرب مساحت پایه و ارتفاع آن است.

V = πr 2 h

مساحت سطح کمی پیچیده تر است، اما می توان آن را به سادگی با گسترش دانش فعلی ما محاسبه کرد. می دانیم که محیط قاعده 2 πr است . بنابراین، اگر به سادگی این فرمول را در h ضرب کنیم، سطح "بشکه" استوانه را خواهیم داشت. اکنون فقط باید مساحت پایه ها را اضافه کنیم که دو برابر مساحت هر یک از پایه های دایره ای است. پس مساحت کل سطح S برابر با زیر است.

S = 2 πrh + πr 2 + πr 2 = 2 ( πrh + πr 2 )

مشکل تمرین : استوانه ای با ارتفاع 16 فوت و شعاع 5 فوت در هر انتها توسط یک نیمکره (نیم کره) پوشیده شده است، همانطور که در زیر نشان داده شده است. مساحت و حجم شکل چقدر است؟

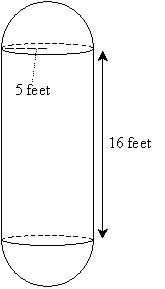
راه حل : ما قبلاً می دانیم که چگونه مساحت ضلع سیلندر را محاسبه کنیم: 2 πrh . همچنین باید مساحت دو کلاهک نیمکره ای را محاسبه کنیم. توجه داشته باشید که "پایه" نیمکره ها مقطعی از کره کامل است. از آنجایی که این مقطع شعاع 5 فوتی دارد، هر دو نیمکره شعاع یکسانی دارند. سطح هر دو نیمکره با هم به سادگی مساحت یک کره کامل به شعاع 5 فوت است. این سطح 4 πr 2 است. اکنون می توانیم مساحت شکل را محاسبه کنیم.

S = 2 π (5) (16) + 4 π (5) 2 = 160 π + 100 π = 260 π ≈ 816.8 فوت 2

برای محاسبه حجم کافی است حجم استوانه به اضافه حجم کره ای به شعاع 5 فوت را بیابید.

فیگورهای مرکب در سه بعدی

برخورد با فیگورهای مرکب در سه بعدی به اصول تقریباً مشابهی نیاز دارد که برای برخورد با فیگورهای مرکب در دوبعد لازم است. به عنوان مثال، محاسبه حجم یک جامد مستطیلی با فضای خالی کروی به سادگی شامل کم کردن حجم کره از حجم کل داخل ناحیه مستطیلی است. همچنین، رویکرد ما برای تقسیم اشکال پیچیده به شکل‌های ساده‌تر و مدیریت آسان‌تر، در مورد فیگورهای سه‌بعدی نیز صدق می‌کند. مسئله تمرینی زیر رویکرد یک شکل سه بعدی را نشان می دهد.

مشکل تمرین : یک منشور مستطیلی شامل دو حفره کروی یکسان به شعاع 2 واحد است، همانطور که در زیر نشان داده شده است. حجم شکل را محاسبه کنید.

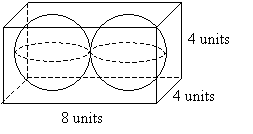
راه حل : ابتدا، بیایید حجم کل درون منشور مستطیلی را محاسبه کنیم. پایه 32 واحد مربع و ارتفاع 4 واحد است. بنابراین حجم 128 واحد مکعب است. شعاع هر کره 2 واحد است. بنابراین، هر یک دارای حجم V زیر است.