دل نوشته ها ی نقش و آموزش ریاضی  

یعنی A = [ a ij ] n×n یک ماتریس متقارن است، سپس a ij = a ji برای همه i و j است .

به عنوان مثال، 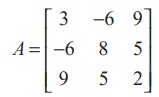یک ماتریس متقارن است زیرا A' =A.

به عنوان مثال، A =

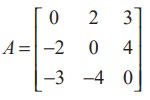
یک ماتریس متقارن کج است زیرا A T = - A است

قضیه 7.1: هر ماتریس مربعی را می توان به صورت مجموع ماتریس های متقارن و ماتریس های متقارن کج نوشت.

برای هر ماتریس مربعی A با ورودی های اعداد حقیقی ، A '+ A یک ماتریس متقارن و A '- A یک ماتریس متقارن چوله است.

Proof

Let B = A + A'.

B' = ( A + A' )' = A' + ( A' )' = A'+ A = A + A' = B .

B ماتریس های متقارن است

C = A − A'

C ' = ( A + ( − A' ))' = A' + ( − A' )' = A' − ( A' )' = A' − A = − ( A − A' ) = − C

C ماتریس های متقارن کج است

و داریم

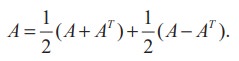
مثال

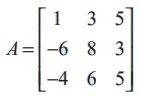
Solution