تفاضل متقارن با استفاده از نمودار ون دو زیرمجموعه A و B یک زیر مجموعه از U است که با A △ B نشان داده می شود و با تعریف می شود.

A △ B = (A - B) ∪ (B - A)

فرض کنید A و B دو مجموعه هستند. تفاضل متقارن دو مجموعه A و B مجموعه (A – B) ∪ (B – A) است و با A △ B نشان داده می شود.

بنابراین، A △ B = (A – B) ∪ (B – A) = {x : x ∉ A ∩ B}

یا، A △ B = {x : [x ∈ A و x ∉ B] یا [x ∈ B و x ∉ A]}

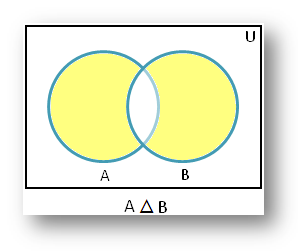
قسمت سایه دار نمودار ون داده شده نشان دهنده  A  △  B است .

A △ B مجموعه تمام آن عناصری است که به A یا B تعلق دارند اما به هر دو تعلق ندارند.

A △ B نیز با (A ∪ B) - (B ∩ A) بیان می شود.

نتیجه این است که A △ ​​∅ = A برای همه زیر مجموعه A،

             A △ A = ∅ برای همه زیر مجموعه A

خواص تفاضل متقارن:

(i) A △ B = B △ A; [ویژگی جابجایی]

(ii) A △ (B △ C) = (A △ B) △ C [ویژگی انجمنی]

مثال برای یافتن تفاضل متقارن با استفاده از نمودار ون :

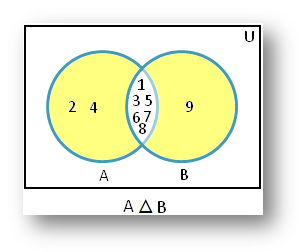
1. اگر A = {1، 2، 3، 4، 5، 6، 7، 8} و B = {1، 3، 5، 6، 7، 8، 9}، آنگاه A - B = {2، 4 }، B – A = {9} و A △ B = {2، 4، 9}.

6صرفه جویی

بنابراین، قسمت سایه دار نمودار ون نشان دهنده A △ ​​B = {2, 4, 9} است.

2. اگر A = {1، 2، 4، 7، 9} و B = {2، 3، 7، 8، 9}، A △ B = {1، 3، 4، 8}

بنابراین، قسمت سایه دار نمودار ون نشان دهنده A △ ​​B = {1، 3، 4، 8} است.

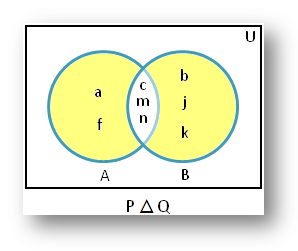
3. اگر P = {a, c, f, m, n} و Q = {b, c, m, n, j, k} پس P△ Q = {a, b, f, j, k}

بنابراین، قسمت سایه دار نمودار ون نشان دهنده P△ Q = {a, b, f, j, k} است.