چند وجهی

در هندسه، چند وجهی یک شکل فضای بسته است که وجه آن چند ضلعی است . کلمه چند وجهی ریشه یونانی دارد که به معنای چهره های متعدد است. در زیر چند نمونه از چند وجهی آورده شده است.

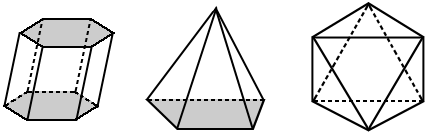
ویژگی های چند وجهی

چند ضلعی هایی که یک چند وجهی را تشکیل می دهند وجه نامیده می شوند. پاره های خط ایجاد شده توسط دو وجه متقاطع را لبه یا یال می گویند. رئوس نقاطی هستند که سه یا چند یال به هم می رسند.

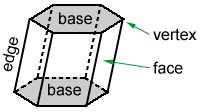
منشور شش ضلعی بالا یک چند وجهی است که دارای 6 وجه جانبی متوازی الاضلاع و 2 وجه در بالا و پایین است که به آنها پایه می گویند که شش ضلعی هستند.

قضیه اویلر

قضیه اویلر رابطه ای بین تعداد وجه ها، رئوس و لبه های یک چندوجهی را نشان می دهد. بیان می کند که مجموع صورت ها و رئوس منهای تعداد یال ها همیشه برابر با دو است:

F + V - E = 2

که در آن F تعداد وجه ها، V تعداد رئوس و E تعداد یال های یک چندوجهی است.

مثال:

برای منشور شش ضلعی نشان داده شده در بالا، F = 8 (شش وجه جانبی + دو پایه)، V = 12، و E = 18:

8 + 12 - 18 = 2

طبقه بندی چند وجهی

چند وجهی را می توان به روش های مختلفی طبقه بندی کرد. به عنوان مثال، آنها را می توان به عنوان چند وجهی منظم و نامنظم طبقه بندی کرد. چندوجهی منتظم، چندوجهی است که وجوه آن همه چند ضلعی های منتظم متجانس هستند. هر چند وجهی که این شرایط را نداشته باشد، نامنظم در نظر گرفته می شود.

چند وجهی را می توان به صورت محدب و مقعر نیز طبقه بندی کرد. یک چندوجهی مقعر حداقل یک وجه دارد که چندضلعی مقعر است. چندوجهی که مقعر نباشد محدب است. چند وجهی را نیز می توان بر اساس تعداد چهره هایی که دارد طبقه بندی کرد. به عنوان مثال، چهار وجهی دارای 4 وجه، پنج وجهی دارای 5 وجه و شش وجهی دارای 6 وجه است.

در زیر لیستی از اصطلاحاتی است که اغلب برای توصیف چندوجهی بر اساس ویژگی های آنها استفاده می شود.

منشورها

منشورها چند وجهی هستند که دارای دو وجه متجانس به نام پایه هستند که در صفحات موازی قرار دارند. یک منشور معمولاً با شکل پایه های چند ضلعی آن نامگذاری می شود. وجوه جانبی (اضلاعی که قاعده نیستند) متوازی الاضلاع ، مستطیل یا مربع هستند .

منشور منظم	منشور نامنظم
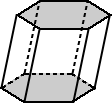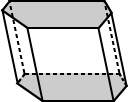پایه های منشور شش ضلعی منتظم بالا دارای پایه هایی هستند که شش ضلعی منظم هستند.	پایه های منشور شش ضلعی بالا شش ضلعی نامنظم هستند.

اهرام

اهرام چند وجهی هستند که قاعده چند ضلعی و مانند سایر وجوه آن مثلث است. یک هرم نیز معمولاً با شکل قاعده چند ضلعی آن نامگذاری می شود.

هرم منظم	هرم نامنظم
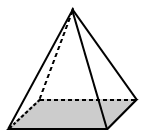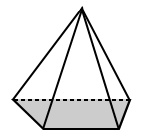قاعده هرم مربع بالا دارای یک قاعده مربع (یک چندضلعی منتظم) است.	پایه هرم ذوزنقه ای بالا یک ذوزنقه با اضلاع نابرابر است (بنابراین یک چندضلعی نامنظم است).

چند وجهی منظم

چند ضلعی منتظم به چندوجهی گفته می شود که وجوه آن همگی چند ضلعی های منتظم هستند. یک چند وجهی منظم بر اساس تعداد وجوه آن نامگذاری می شود. فقط پنج چند وجهی وجود دارد که چندوجهی منظم هستند. به این جامدات افلاطونی می گویند.

پنج جامد افلاطونی

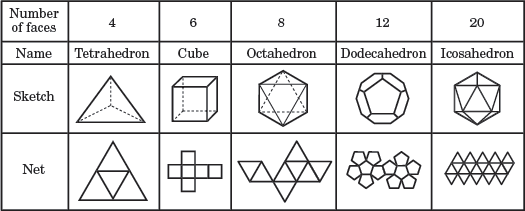
در نمودار بالا، هر چند وجهی منظم بر اساس تعداد وجوه آن نامگذاری شده است. شبکه زیر هر طرح تصویری دوبعدی از تمام چهره‌های چند وجهی را نشان می‌دهد.

اکثر منشورهای منظم معمولاً چند وجهی منظم در نظر گرفته نمی شوند. مکعب منشور تنها به طور منظم که همچنین می تواند به عنوان یک جسم چند وجهی منظم طبقه بندی شده است.

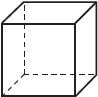
به همین ترتیب، چهار وجهی منتظم تنها هرم منظمی است که 4 وجه منظم نیز دارد.