دل نوشته ها ی نقش و آموزش ریاضی  

وقتی یک شکل 90 درجه در خلاف جهت عقربه‌های ساعت می‌چرخانیم، هر نقطه از شکل داده شده باید از

(x, y) به (-y, x)

تغییر کند و شکل چرخش شده را نمودار کنیم.

مثال 1: 

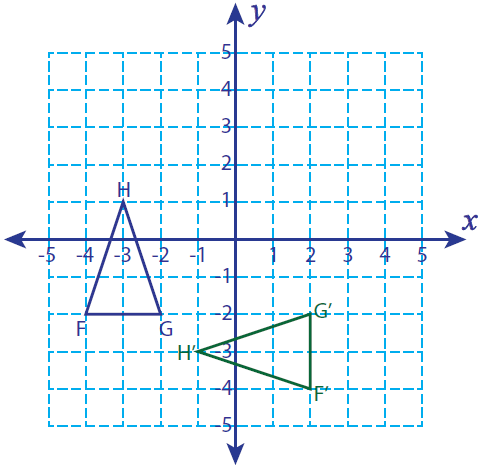
فرض کنید F (-4، -2)، G (-2، -2) و H (-3، 1) سه رأس یک مثلث باشند. اگر این مثلث 90 درجه خلاف جهت عقربه های ساعت بچرخد، رئوس شکل و نمودار چرخانده شده را پیدا کنید.

راه حل : 

مرحله 1:

در اینجا مثلث 90 درجه خلاف جهت عقربه های ساعت می چرخد. بنابراین قانونی که باید در اینجا اعمال کنیم این است

(x، y) -------> (-y، x)

گام 2 :

بر اساس قانون داده شده در مرحله 1، باید رئوس شکل چرخیده را پیدا کنیم.

مرحله 3:

(x , y) -----> (-y , x)

F(-4، -2) -------> F'(2، -4)

G(-2، -2) -------> G'(2، -2)

H (-3، 1) -------> H'(-1، -3)

مرحله 4:

رئوس شکل چرخیده هستند        

F'(2، -4)، G'(2، -2) و H'(-1، -3) 

مثال 2: 

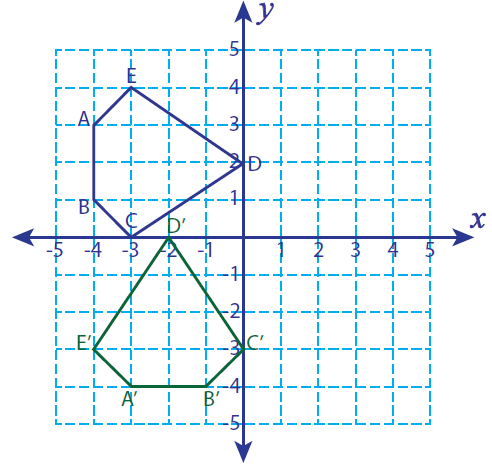
فرض کنید A (-4، 3)، B (-4، 1)، C (-3، 0)، D (0، 2) و E (-3،4) رئوس یک شکل بسته باشند. اگر این شکل 90 درجه خلاف جهت عقربه های ساعت می چرخد، رئوس شکل چرخیده و نمودار را پیدا کنید.

راه حل : 

مرحله 1:

در اینجا مثلث 90 درجه خلاف جهت عقربه های ساعت می چرخد. بنابراین قانونی که باید در اینجا اعمال کنیم این است

(x، y) -------> (-y، x)

گام 2 :

بر اساس قانون داده شده در مرحله 1، باید رئوس شکل چرخیده را پیدا کنیم.

مرحله 3:

(x، y) -----> (-y، x)

A(-4، ​​3) -------> A'( -3، -4)

B(-4، 1) -------> B'(-1، -4)

C(-3، 0) -------> C'(0، -3)

D(0, 2) -------> D'(-2, 0)

E(-3، 4) -------> E'(-4، -3)

مرحله 4:

رئوس شکل چرخیده هستند        

A'(-3، -4)، B'(-1، -4)، C'(0، -3)، D'(-2، 0) و E'(-4، -3)

مثال 3: 

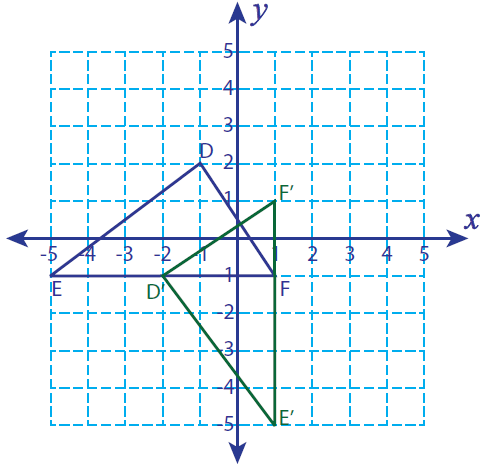
فرض کنید D (-1، 2)، E (-5، -1) و F (1، -1) رئوس یک مثلث باشند. اگر مثلث 90 درجه خلاف جهت عقربه های ساعت بچرخد، رئوس شکل و نمودار چرخانده شده را پیدا کنید. .

راه حل : 

مرحله 1:

در اینجا مثلث 90 درجه خلاف جهت عقربه های ساعت می چرخد. بنابراین قانونی که باید در اینجا اعمال کنیم این است

(x، y) -------> (-y، x)

گام 2 :

بر اساس قانون داده شده در مرحله 1، باید رئوس شکل چرخیده را پیدا کنیم.

مرحله 3:

(x، y) -----> (-y، x)

D(-1، 2) -------> D'(-2، -1)

E(-5، -1) -------> E'(1، -5)

F(1، -1) -------> F'(1، 1)

مرحله 4:

رئوس شکل چرخیده هستند        

D'(-2، -1)، E'(1، -5) و F'(1، 1)

مثال 4: 

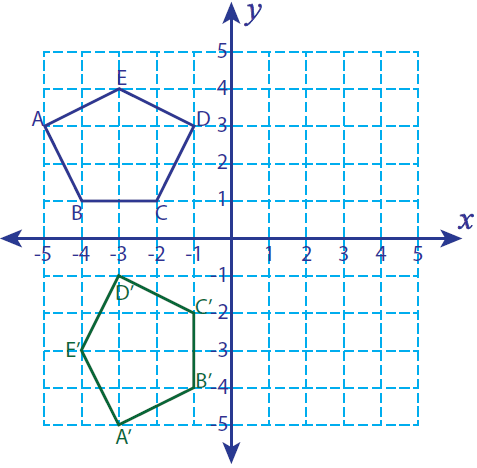
فرض کنید A (-5، 3)، B (-4، 1)، C (-2، 1) D (-1، 3) و E (-3، 4) رئوس یک شکل بسته باشند. اگر این شکل 90 درجه خلاف جهت عقربه های ساعت می چرخد، رئوس شکل چرخیده و نمودار را پیدا کنید.

راه حل : 

مرحله 1:

در اینجا مثلث 90 درجه خلاف جهت عقربه های ساعت می چرخد. بنابراین قانونی که باید در اینجا اعمال کنیم این است

(x، y) -------> (-y، x)

گام 2 :

بر اساس قانون داده شده در مرحله 1، باید رئوس شکل چرخیده را پیدا کنیم.

مرحله 3:

(x، y) -----> (-y، x)

A(-5، 3) -------> A'(-3، -5)

B(-4، 1) -------> B'(-1، -4)

C(-2، 1) -------> C'(-1، -2)

D(-1، 3) -------> D'(-3، -1)

E(-3، 4) -------> E'(-4، -3)

مرحله 4:

رئوس شکل چرخیده هستند        

A'(-3، -5)، B'(-1، -4)، C'(-1، -2)، D'(-3، -1) و E'(-4، -3) 

مثال 5: 

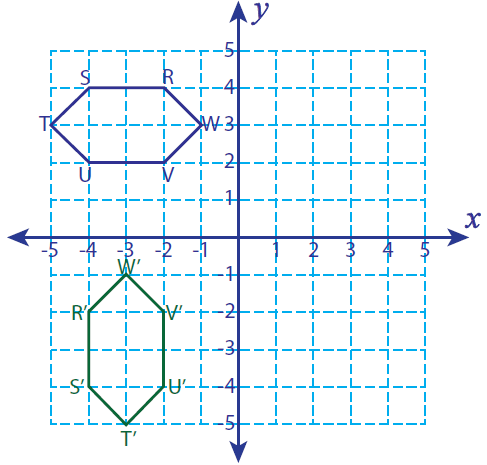
فرض کنید R (-2، 4)، S (-4، 4)، T (-5، 3) U (-4، 2) و V (-2، 2) رئوس یک شکل بسته باشند. اگر این شکل 90 درجه خلاف جهت عقربه های ساعت می چرخد، رئوس شکل چرخیده و نمودار را پیدا کنید.

راه حل : 

مرحله 1:

در اینجا مثلث 90 درجه خلاف جهت عقربه های ساعت می چرخد. بنابراین قانونی که باید در اینجا اعمال کنیم این است

(x، y) -------> (-y، x)

گام 2 :

بر اساس قانون داده شده در مرحله 1، باید رئوس شکل چرخیده را پیدا کنیم

مرحله 3:

(x، y) -----> (-y، x)

R(-2، 4) -------> R'(-4، -2)

S(-4، 4) -------> S'(-4، -4)

T(-5، 3) -------> T'(-3، -5)

U(-4، 2) -------> U'(-2، -4)

V(-2، 2) -------> V'(-2، -2)

مرحله 4:

رئوس شکل چرخیده هستند        

R'(-4، -2)، S'(-4، -4)، T'(-3، -5)، U'(-2، -4) وV'(-2، -2)