- 90∘:R90∘(x,y)=(−y,x)
- 180∘:R180∘(x,y)=(−x,−y)
- 270∘:R270∘(x,y)=(y,−x)
در این درس ها یاد خواهیم گرفت
در تبدیل انعکاس ، تمام نقاط یک جسم بر روی خطی به نام محور انعکاس یا خط بازتاب منعکس یا برعکس می شوند.
مثال: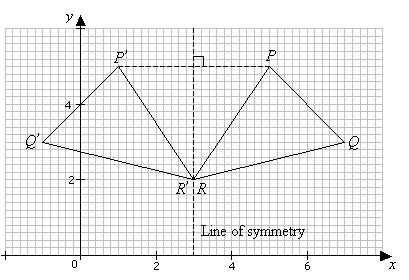
بازتاب با محور تقارن یا خط آینه ای تعریف می شود . در نمودار بالا، خط آینه x = 3 است.
تحت بازتاب، شکل و اندازه یک تصویر دقیقاً مشابه شکل اصلی است. به این نوع تبدیل، تبدیل ایزومتریک می گویند .
جهت گیری به صورت جانبی معکوس است ، یعنی آنها در جهت مخالف هستند.
خط بازتاب عمود بر خطی است که به هر نقطه و تصویر آن می پیوندد (مثلاً PP ' در شکل بالا).
تمام نقاط روی خط آینه تغییر نمی کند. گفته می شود این نقاط ثابت هستند. (R یک نقطه ثابت در بالا است.)
اگر محور انعکاس روی یکی از خطوط شبکه باشد، فقط تعداد مربع ها را از یک نقطه روی جسم تا محور می شماریم و تصویر به همان اندازه از محور فاصله دارد.
مثال:
در نمودار، شکل A در خط XY منعکس شده است. تصویر A را در نمودار رسم کنید.
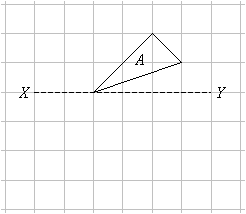
راه حل: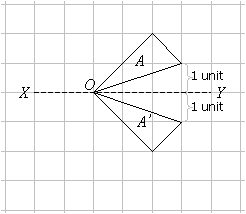
توجه داشته باشید که نقطه O در زیر بازتاب بدون تغییر باقی می ماند زیرا روی محور انعکاس قرار دارد. هر نقطه در خط بازتاب بدون تغییر است - چنین نقاطی به عنوان ثابت توصیف می شوند.
نحوه انعکاس شکل بر روی کاغذ مربعی بدون استفاده از کاغذ ردیابی
این ویدئو نحوه انعکاس شکل را بر روی کاغذ مربع بدون استفاده از کاغذ ردیابی نشان می دهد. فقط فاصله هر گوشه تا خط آینه را بشمارید و همان فاصله را از خط آینه بشمارید. هنگامی که تمام نقاط آنها منعکس شدند، با استفاده از خط کش خود، نقاط را به طور منظم به بالا وصل کنید.
اگر محور انعکاس روی خطوط شبکه نباشد، برای ساخت تصویر باید از قطب نما استفاده کنیم.
مثال: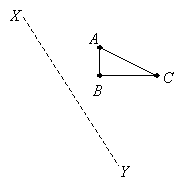
در نمودار زیر، مثلث ABC در خط XY منعکس شده است. تصویر مثلث را در نمودار رسم کنید.
راه حل:
مرحله 1: نقطه تیز پرگار را در A قرار دهید و دو کمان را که خط XY را قطع می کنند رسم کنید.

مرحله 2: نقطه تیزپرگاررا در اولین نقطه متقاطع قرار دهید و یک قوس در طرف مقابل XY علامت بزنید. نقطه تیز پرگار را روی نقطه متقاطع دوم قرار دهید و یک قوس علامت بزنید تا با قوس اول قطع شود. تقاطع تصویر' A است.
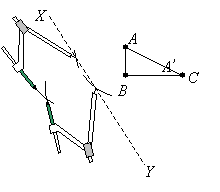
مرحله 3: مراحل 1 و 2 را برای بدست آوردن نقاط B و C تکرار کنید. نقاط 'A ' ، B و 'C را به هم بپیوندید تا تصویر 'A ' B ' C را به دست آورید.

ساختن انعکاس با دست
چگونه با استفاده از یک خط کش یک شکل را روی یک خط با دست منعکس کنیم.
چگونه یک خط بازتاب بسازیم؟
با توجه به جسم و تصویر یک خط بازتاب بسازید.
اکنون به نحوه انعکاس نقاط و اشکال در صفحه مختصات خواهیم پرداخت. هنگامی که نقاط بر روی خطوط مختلف بازتاب منعکس می شوند، توجه به الگوهای مختصات مفید خواهد بود.
قوانین مختصات برای انعکاس
اگر (a, b) روی محور x منعکس شود، تصویر آن نقطه (a, -b) است.
اگر (a, b) روی محور y منعکس شود، تصویر آن نقطه (a، b-) است.
اگر (a، b) روی خط y = x منعکس شود، تصویر آن نقطه (b، a)است. اگر (a، b) روی خط y = -x منعکس شود، تصویر آن نقطه
(-b، a)
است.
بازتاب
یک ایزومتری است، به این معنی که اصل و تصویر مطابق هستند، برای انجام یک بازتاب هندسی، یک خط بازتاب مورد نیاز است. جهت گیری حاصل از دو شکل مخالف است. قسمت های متناظر شکل ها به همان اندازه از خط بازتاب فاصله دارند.
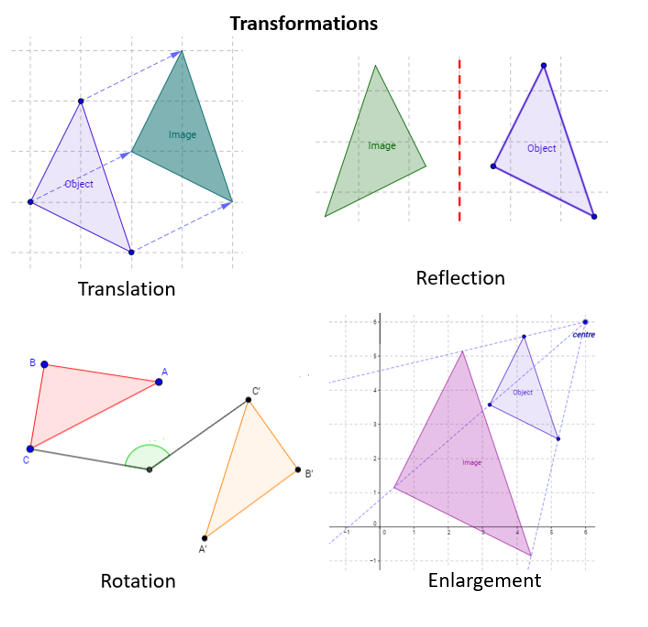
(x,y)→(x+5,y+3).
(x,y)→(x−2,y+3)
مربع S(1,2),Q(4,1),R(5,4) وE(2,5) .
( x ، y) → ( x + 6 , y- 4 ).
تبدیل تجانس یکی از چهار نوع تبدیل در هندسه است.
تجانس تغییر شکلی است که تصویری مشابه شکل اصلی، اما اندازه متفاوت ایجاد می کند. ایزومتری نیست ارقام مشابه را تشکیل می دهد.
به عبارت ساده، تجانس به این معنی است که فقط شکل داده شده را بدون چرخش یا هر چیز دیگری اندازه گیری می کند.
تجانس فاکتور مقیاس " k" :
(x، y) -----> ( k x، k y)
هنگامی که دانش آموزان قانون ذکر شده در بالا را که باید برای تبدیل تجانس اعمال کنند را درک کنند، می توانند به راحتی یک شکل را تغییر شکل دهند.
برای مثال، اگر بخواهیم تبدیل تجانس نقطه (5، 3) را برای ضریب مقیاس "k = 2" انجام دهیم، پس از تبدیل، نقطه (10، 6) خواهد بود.
در اینجا، قانونی که ما اعمال کرده ایم این است
(x، y) -------> (kx، ky)
برای k = 2، به دست می آوریم
(5، 3) -------> (10، 6)
برای درک بهتر، مثال زیر را در نظر می گیریم.
سوال:
فرض کنید A(-2، -2)، B(-1، 2) و C(2، 1) سه رأس یک مثلث باشند. اگر این مثلث برای ضریب مقیاس "k = 2" گشاد شود، رئوس جدید A'، B' و C' چه خواهند بود؟
راه حل:
مرحله 1:
ابتدا باید قانون صحیحی را که باید در این مشکل اعمال کنیم، بدانیم.
گام 2 :
در اینجا، مثلث برای ضریب مقیاس "k = 2" گشاد شده است.
بنابراین، قانونی که باید در اینجا اعمال کنیم این است
(x, y) -------> (kx , ky)
مرحله 3:
بر اساس قانون داده شده در مرحله 1، باید رئوس مثلث گشاد شده A'B'C' را پیدا کنیم.
مرحله 4:
(x، y) -----> (kx، ky)
A(-2، -2) -------> A'(-4، -4)
B(-1، 2) -------> B'(-2، 4)
C(2، 1) -------> C'(4، 2)
مرحله 5:
رئوس مثلث متسع هستند
A'(-4، -4)، B(-2، 4) و C'(4، 2)
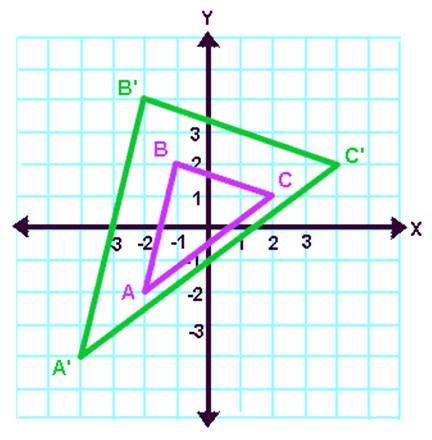
1. ابتدا باید رئوس تصویر پیش را رسم کنیم.
2. در مسئله فوق رئوس تصویر پیشین هستند
A(-2، -2)، B(-1، 2) و C(2، 1)
3. وقتی این نقاط را روی یک کاغذ گراف رسم می کنیم، شکل پیش تصویر (شکل اصلی) به دست می آید.
4. وقتی شکل داده شده را برای "k = 2" گشاد می کنیم، باید فرمول را اعمال کنیم
(x، y) -------> (kx، ky)
5. زمانی که فرمول را اعمال می کنیم، رئوس تصویر زیر را بدست می آوریم (شکل گشاد شده).
6. در مسئله فوق رئوس تصویر هستند
A'(-4، -4)، B'(-2، 4) و C'(4، 2)
7. وقتی این نقاط را روی کاغذ گراف رسم می کنیم، شکل تصویر (شکل گشاد شده) را به دست می آوریم.
مرکز تجانس می تواند داخل یا خارج تصویر اصلی و تصویر گشاد شده باشد. مرکز تجانس می تواند در هر نقطه ای از صفحه مختصات باشد تا زمانی که خطوطی که هر جفت رئوس متناظر را بین تصویر اصلی و گشاد شده به هم متصل می کنند در مرکز تجانس قطع می کنند.
مثال 1:
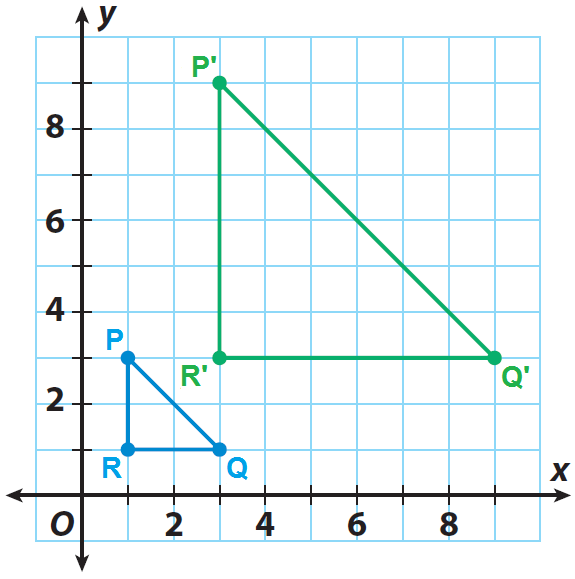
مثلث PQR نشان داده شده در شبکه، تصویر قبلی است. اگر مرکز تجانس مبدأ و ضریب مقیاس 3 باشد، تصویر گشاد شده P'Q'R' را رسم کنید.
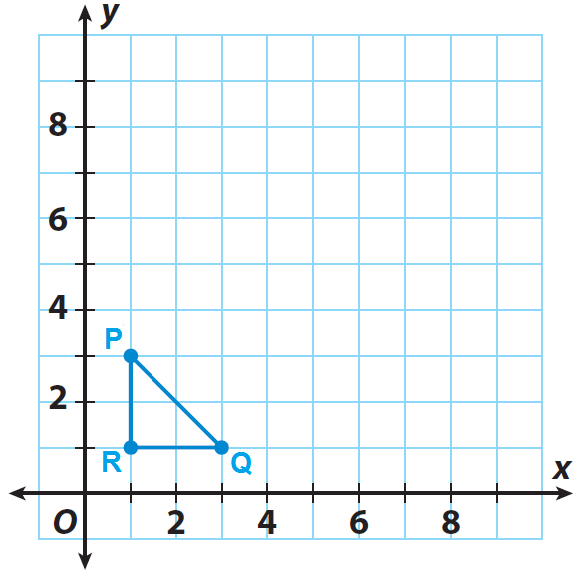
راه حل :
مرحله 1:
مختصات رئوس تصویر پیش را فهرست کنید.
P(1، 3)، Q(3، 1) و R(1، 1)
گام 2 :
از آنجایی که ضریب مقیاس 3 است، قانون به دست آوردن مختصات رئوس تصویر است
(x، y) → (3x، 3y)
مرحله 3:
مختصات رئوس تصویر را فهرست کنید.
P(1، 3) ---> P'(3، 9)
Q(3، 1) ---> Q'(9، 3)
R(1، 1) ---> R'(3، 3)
مرحله 4:
تصویر P'Q'R را رسم کنید.
مثال 2:
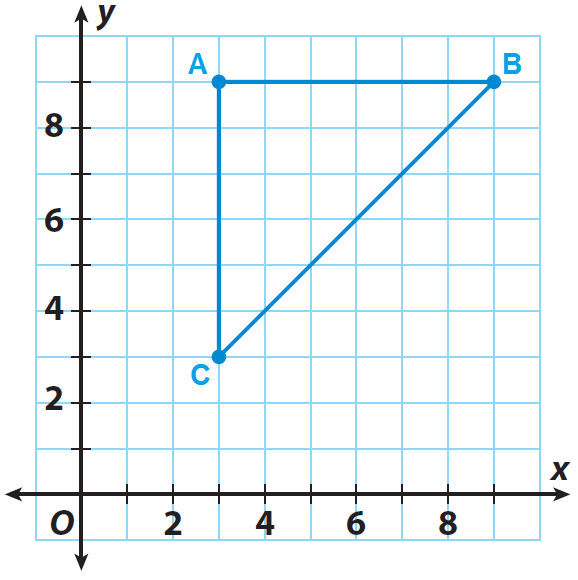
مثلث ABC نشان داده شده در شبکه، تصویر پیشین است. اگر مرکز تجانس مبدا و ضریب مقیاس 1/3 باشد، تصویر گشاد شده A'B'C' را رسم کنید.
راه حل :
مرحله 1:
مختصات رئوس تصویر پیش را فهرست کنید.
A(3، 9)، B (9، 9) و C (3، 3)
گام 2 :
از آنجایی که ضریب مقیاس 1/3 است، قانون به دست آوردن مختصات رئوس تصویر است
(x، y) → [(1/3)x، (1/3)y]
مرحله 3:
مختصات رئوس تصویر را فهرست کنید.
A(3، 9) ---> A'(1، 3)
B (9، 9) ---> B'(3، 3)
C(3، 3) ---> C'(1، 1)
مرحله 4:
تصویر A'B'C را رسم کنید.
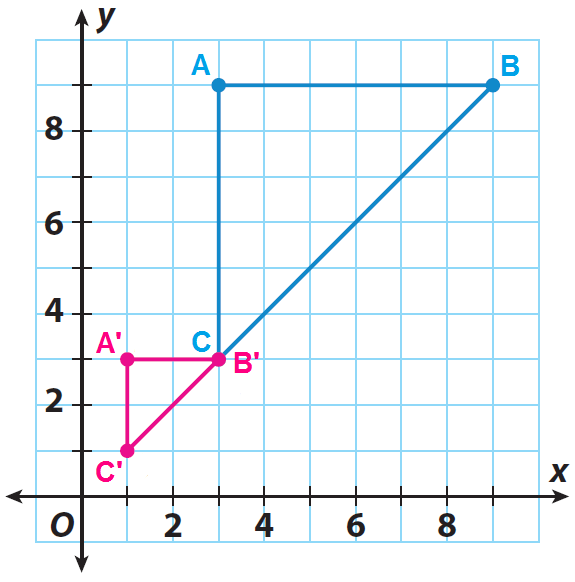
مثال 3:
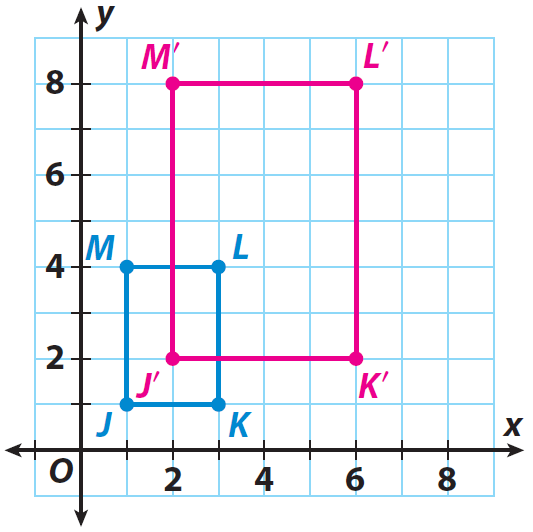
مستطیل JKLM که روی شبکه نشان داده شده است، تصویر قبلی است. اگر مرکز تجانس مبدا و ضریب مقیاس 2 باشد، تصویر متسع J'K'L'M' را رسم کنید.
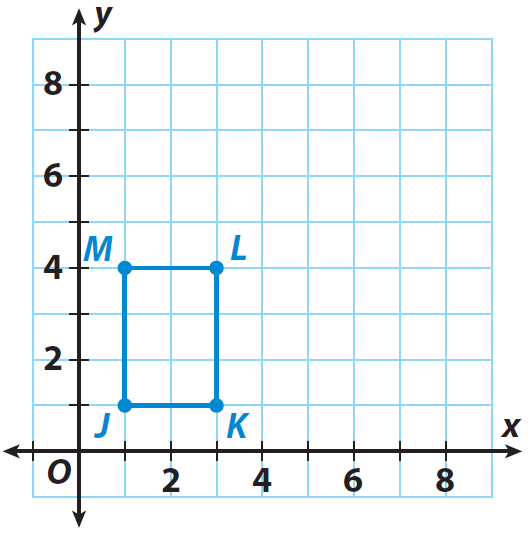
راه حل :
مرحله 1:
مختصات رئوس تصویر پیش را فهرست کنید.
J(1، 1)، K (3، 1)، L (3، 4) و M(1، 4)
گام 2 :
از آنجایی که ضریب مقیاس 2 است، قانون به دست آوردن مختصات رئوس تصویر است
(x، y) → (2x، 2y)
مرحله 3:
مختصات رئوس تصویر را فهرست کنید.
J(1، 1) ---> J'(2، 2)
K (3، 1) ---> K'(6، 2)
L(3، 4) ---> L'(6، 8)
M(1، 4) ---> M'(2، 8)
مرحله 4:
تصویر J'K'L'M' را رسم کنید.
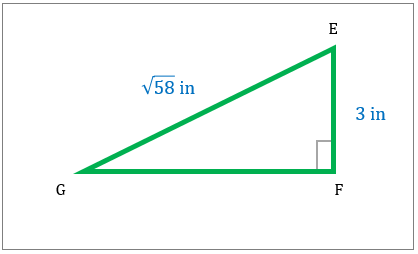
مثلث قائم الزاویه نشان داده شده است. مساحت این شکل را مشخص کنید.
 |
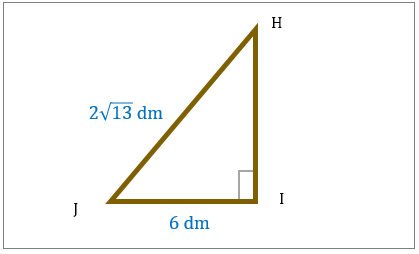
مساحت مثلث قائم الزاویه را در تصویر زیر بیابید.
 |
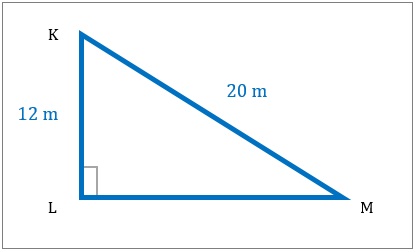
با کمک قضیه فیثاغورث، که با مساحت مثلث مطابقت دارد؟
 |
مثلث قائم الزاویه را تحلیل کنید و مساحت آن را محاسبه کنید.
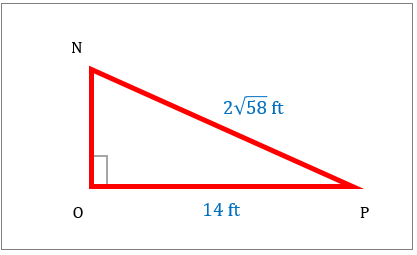 |
پاسخ به انتخاب ها
مساحت مثلث قائم الزاویه ساخته شده را در نمودار با استفاده از قضیه فیثاغورث تعیین کنید.
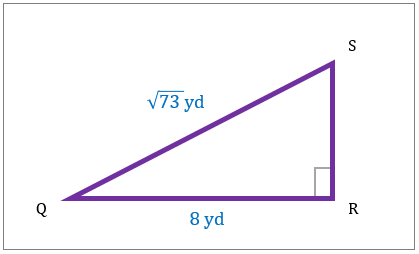 |
مثلث قائم الزاویه را در نظر بگیرید و مساحت آن را حل کنید.
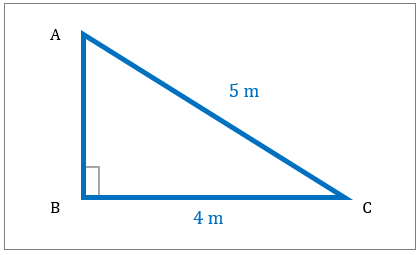 |
مساحت مثلث قائم الزاویه را که در زیر نشان داده شده است محاسبه کنید.
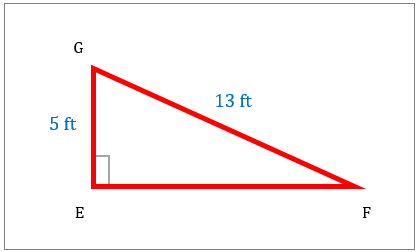 |
مثلث قائم الزاویه در زیر نشان داده شده است. مساحت این شکل را مشخص کنید.
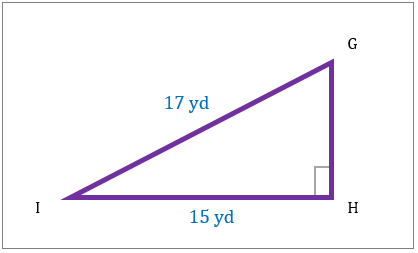 |
مساحت مثلث قائم الزاویه را در تصویر زیر بیابید.
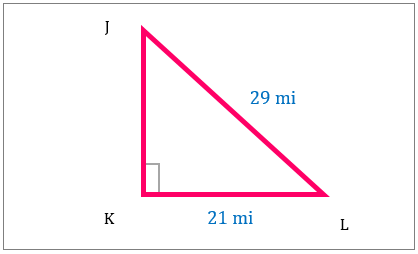 |
با کمک قضیه فیثاغورث، مساحت مثلث کدام است؟
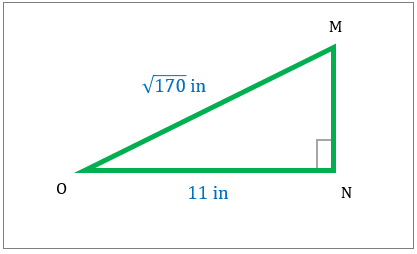 |
مثلث قائم الزاویه را تحلیل کنید و مساحت آن را محاسبه کنید.
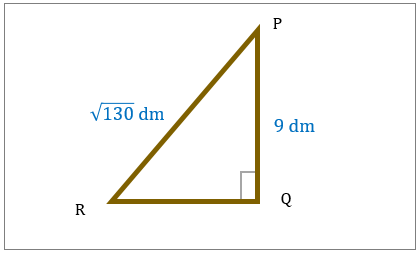 |
مساحت مثلث قائم الزاویه ساخته شده را در نمودار با استفاده از قضیه فیثاغورث تعیین کنید.
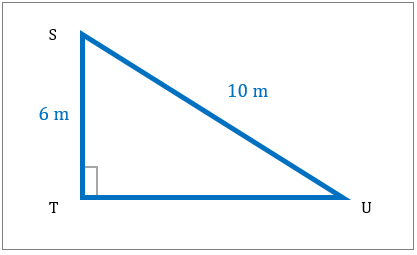 |
به مثلث در زیر مراجعه کنید. مساحت شکل نشان داده شده چقدر است؟
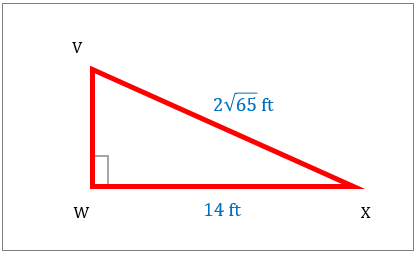 |
مثلث قائم الزاویه را در نظر بگیرید و مساحت آن را حل کنید.
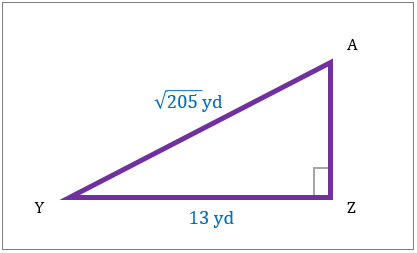 |
مساحت مثلث قائم الزاویه را که در زیر نشان داده شده است، محاسبه کنید.
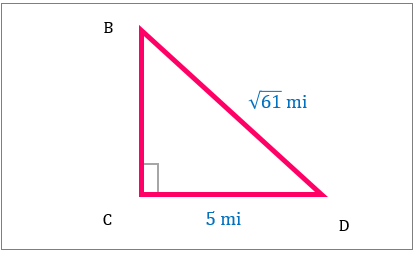 |
مساحت مثلث قائم الزاویه ساخته شده را در نمودار با استفاده از قضیه فیثاغورث تعیین کنید.
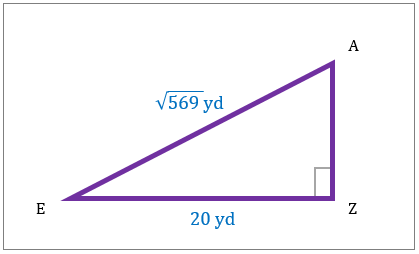 |
مثلث قائم الزاویه تحلیل کنید و مساحت آن را محاسبه کنید.
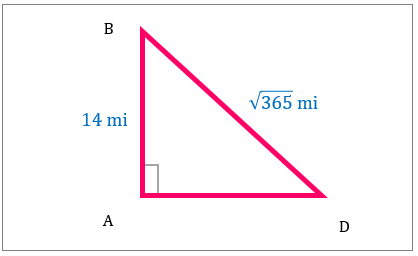 |
با کمک قضیه فیثاغورث، مساحت مثلث کدام است؟
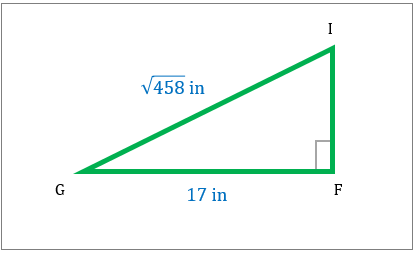 |
مساحت مثلث قائم الزاویه را در تصویر زیر بیابید.
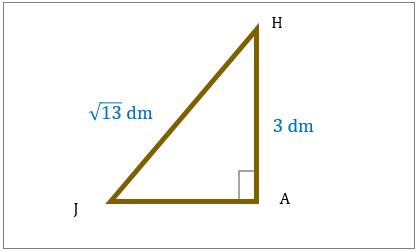 |
مثلث قائم الزاویه در زیر نشان داده شده است. مساحت این شکل را مشخص کنید.
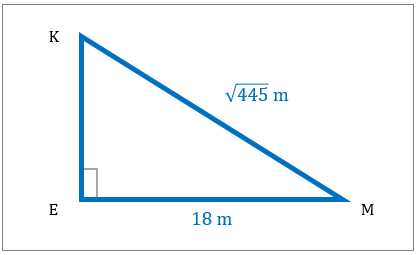 |
مساحت مثلث قائم الزاویه را که در زیر نشان داده شده است، محاسبه کنید.
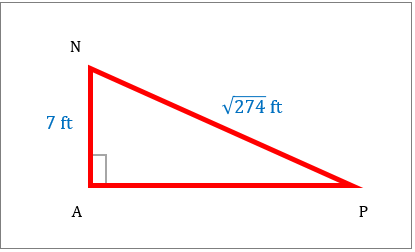 |
مثلث قائم الزاویه را برای مساحت آن در نظر بگیرید.
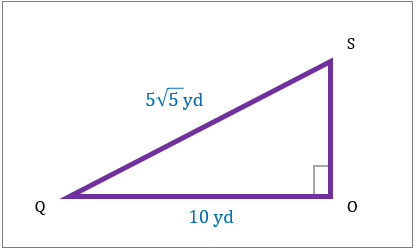 |
مثلث قائم الزاویه در زیر نشان داده شده است. مساحت این شکل را مشخص کنید.
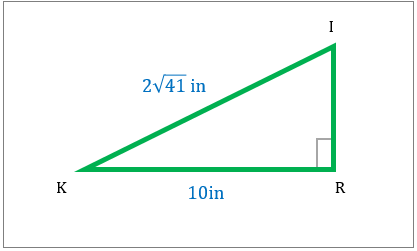 |
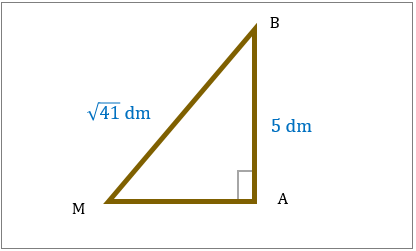 |
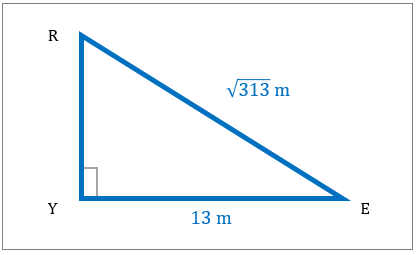
مثلث قائم الزاویه در زیر نشان داده شده است. مساحت این شکل را مشخص کنید.
 |
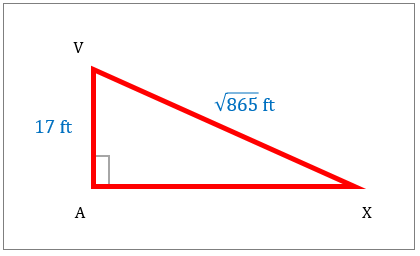 |
مساحت مثلث قائم الزاویه ساخته شده در نمودار با استفاده از قضیه فیثاغورث تعیین کنید.
 |
مثلث قائم الزاویه را تحلیل کنید و مساحت آن را محاسبه کنید.
 |
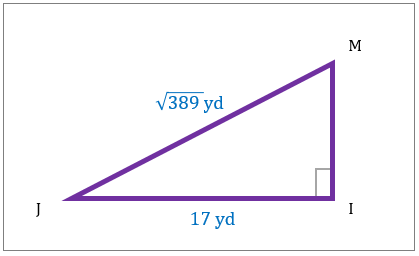
با کمک قضیه فیثاغورث، مساحت مثلث کدام است؟
 |
مساحت مثلث قائم الزاویه را در تصویر زیر بیابید.
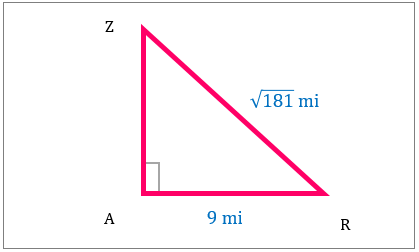 |
مساحتی که با اضلاع مستطیل محدود شده است، با داشتن مختصات رئوس آن در شکلی که نقطه B در مبدأ آن قرار دارد، محدود شده است؟
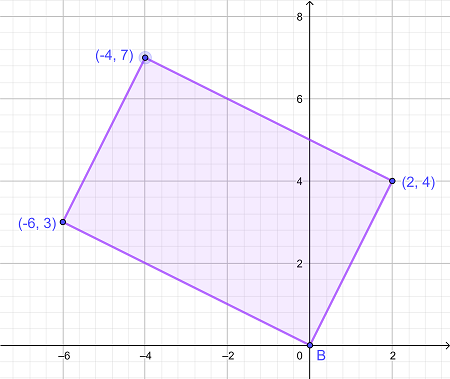 |
پاسخ به انتخاب ها
اگر مختصات راس B (2-، -15) و برای راس D (-3، -2) باشد ، مساحت مستطیل شکل زیر را بیابید .
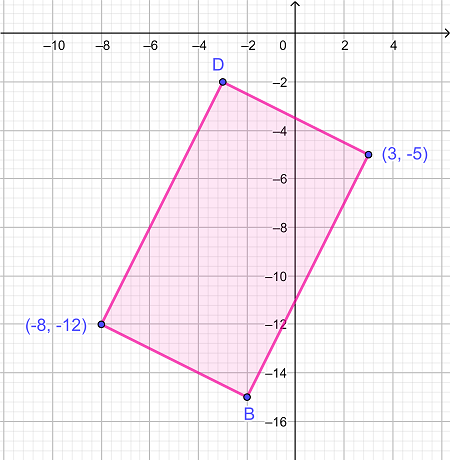 |
پاسخ صحیح را برای مساحت مستطیل زیر انتخاب کنید.
 |
اگر مختصات هر رأس به صورت زیر باشد، مساحت محدود شده با مستطیل زیر را تعیین کنید:
W = (-6، 1)
X = (-2، -2)
Y = (4، 6)
Z = (0، 9)
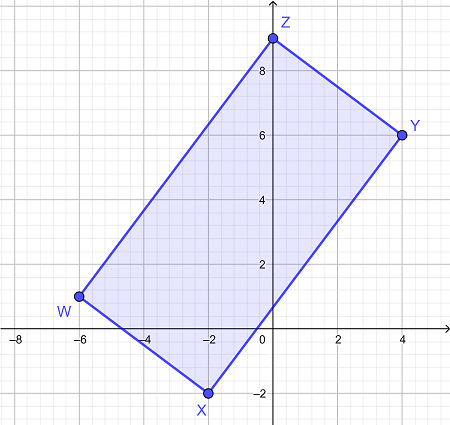 |
پاسخ به انتخاب ها
مساحت شکل مستطیلی که در شکل زیر نشان داده شده است چقدر است؟
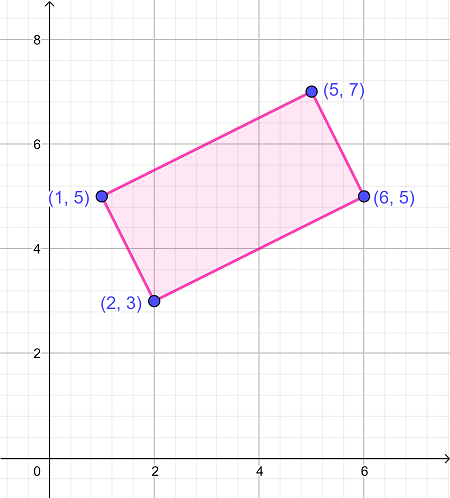 |
مساحت مستطیل LOAF را در یک صفحه مختصات در صورتی حل کنید که رئوس آن در مختصات زیر باشد:
L = (-4، 2)
O = (-3، 0)
A = (3، 3)
F = (2، 5)
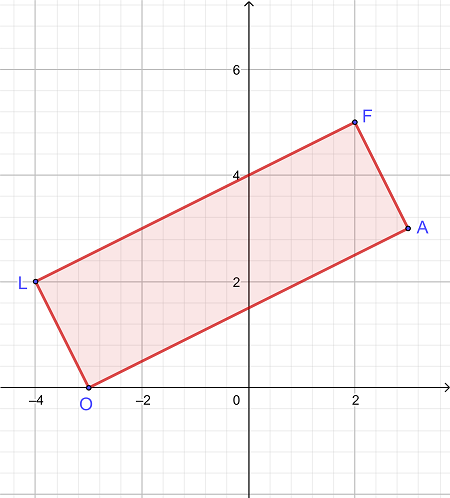 |
پاسخ به انتخاب ها
مساحت مستطیل را در صفحه مختصات دکارتی زیر محاسبه کنید اگر مختصات نقطه A و C به صورت زیر باشد:
A = (-12، 0)
C = (-1، -3)
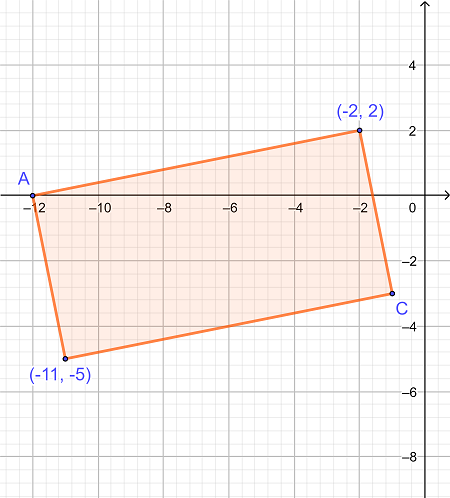 |
مساحت مستطیل در شکل داده شده را حل کنید.
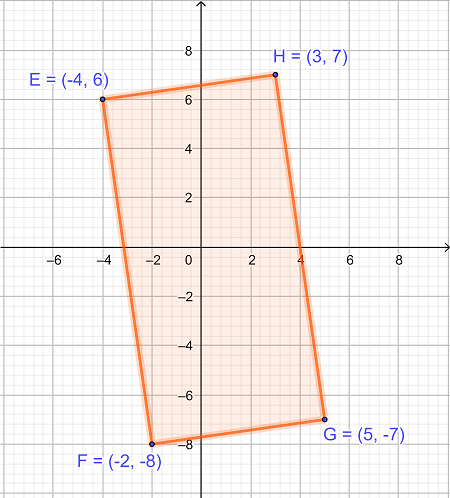 |
مساحت ناحیه سایهدار را که در شکل زیر نشان داده شده است، تعیین کنید.
 |
مساحت مستطیل را در شکل داده شده در صورتی تعیین کنید که رئوس آن به صورت زیر باشد:
P = (-1، -3)
Q = (4، -8)
R = (11, -1)
S = (6، 4)
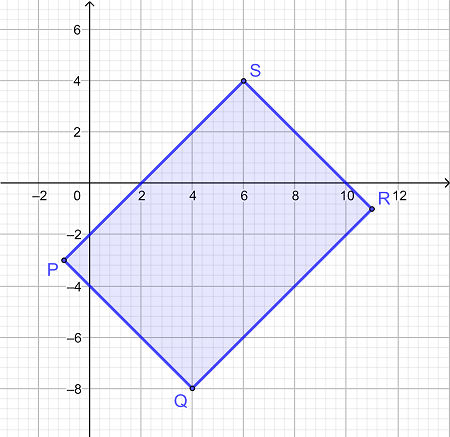 |
مساحت محدود شده با مستطیل TUVW زیر را محاسبه کنید.
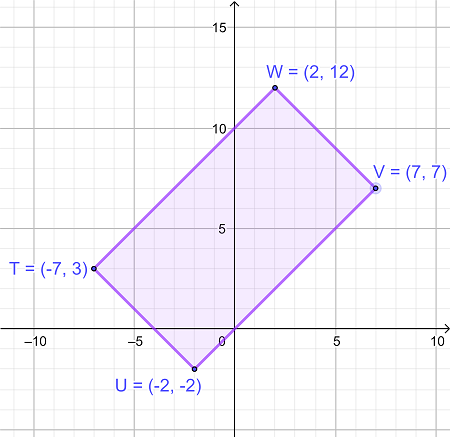 |
مساحت شکل مستطیلی در شکل زیر چقدر است؟
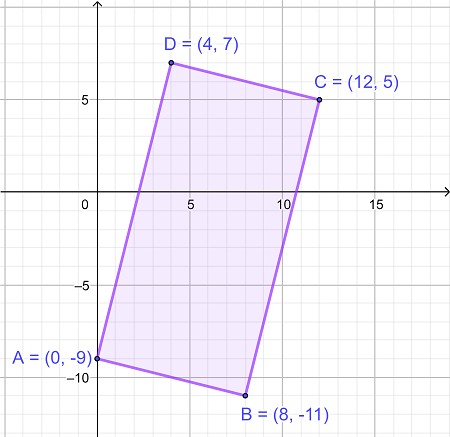 |
مساحت محدود شده توسط مستطیل را در صفحه مختصاتی که در شکل زیر نشان داده شده است محاسبه کنید.
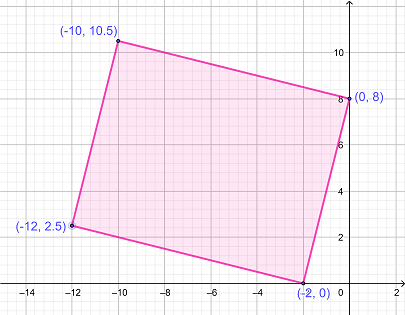 |
اگر مختصات نقطه A و C به ترتیب (8-, -2) و (0, -1) باشد مساحت مستطیل ABCD را تعیین کنید.
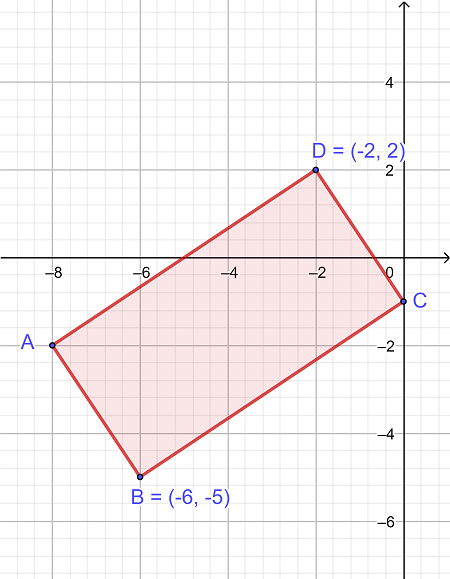 |
اگر مختصات هر رأس در زیر نشان داده شود، مساحت مستطیل در یک صفحه مختصات چقدر است؟
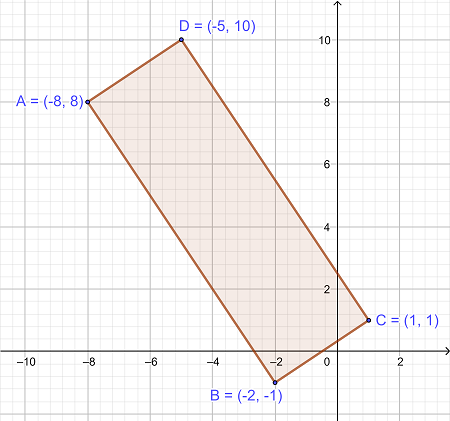 |
مساحت مستطیل ABCD را در صفحه مختصات تعیین کنید اگر رئوس به صورت زیر قرار گیرند:
A = (-5، -3)
B = (-1، -9)
C = (8، -3)
D = (4، 3)
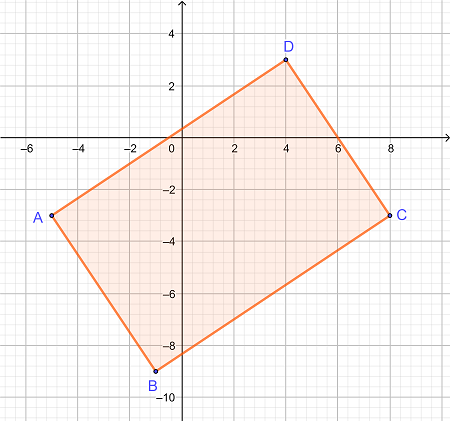 |
مقدار صحیح مساحت ناحیه سایه دار مستطیلی را همانطور که در شکل زیر نشان داده شده است، پیدا کنید.
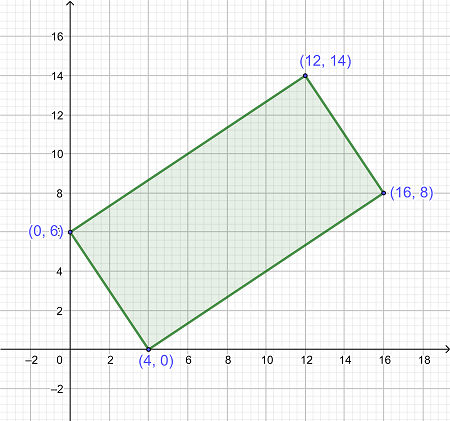 |
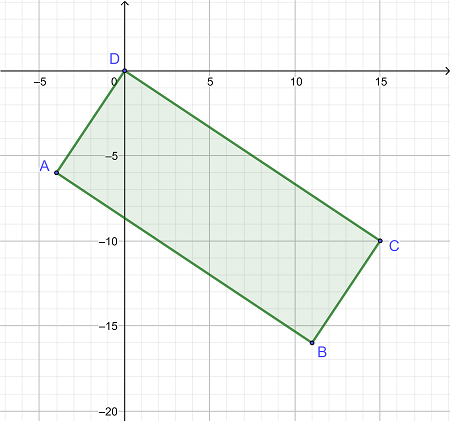
مساحت مستطیل داده شده را در صورتی محاسبه کنید که مختصات رئوس آن به صورت زیر باشد:
A = (-4، -6)
B = (11، -16)
C = (15، -10)
D = (0، 0)
 |
پاسخ به انتخاب ها
مساحت محصور در شکل مستطیلی در شکل چقدر است؟
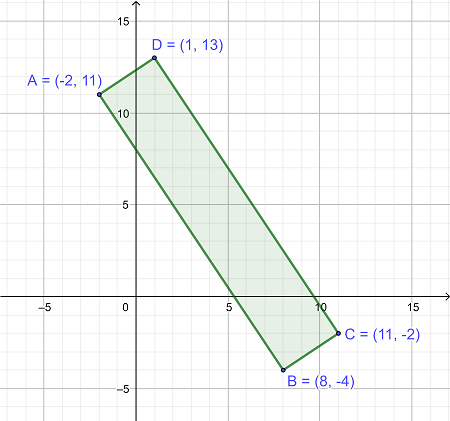 |
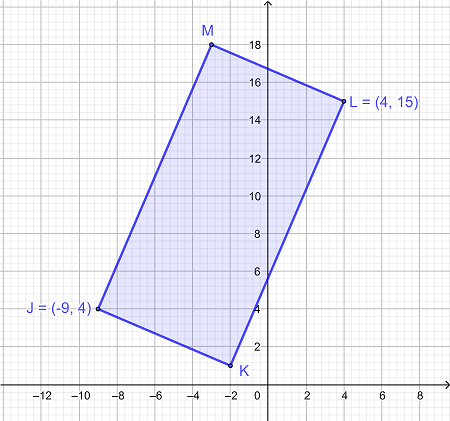
اگر مختصات نقطه M (3-، 18) و نقطه K (2-، 1) باشد، مساحت مستطیل زیر را پیدا کنید.
 |
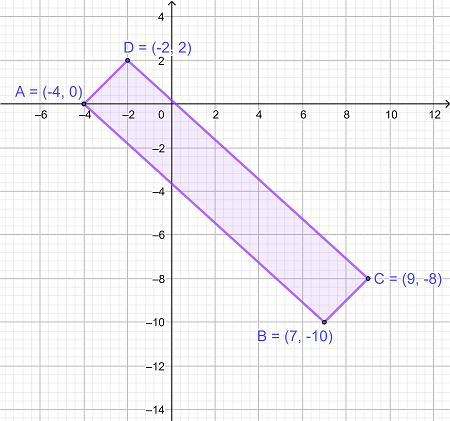
مساحت محدود شده با مستطیل ABCD را مطابق شکل زیر حل کنید.
 |
مختصات رئوس P، Q، R و S به ترتیب (-13، -13)، (-7، -17)، (5، 1) و (-1، 5) است. مساحت مستطیل تشکیل شده توسط آن مختصات را تعیین کنید.
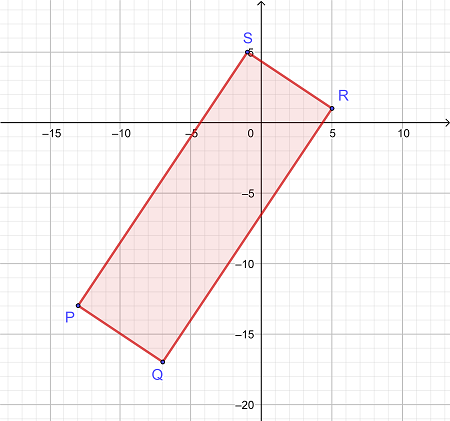 |
 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.