چند وجهی

چند وجهی یک شکل سه بعدی است که دارای صورت های صاف، لبه های مستقیم و راس های تیز (گوشه ها) است. کلمه "polyhedron" از یک کلمه یونانی گرفته شده است، که در آن "poly" به معنای "تعدادی" و hedron به معنای "وجه" است. بنابراین، هنگامی که بسیاری از سطوح صاف به یکدیگر متصل می شوند، یک چند وجهی را تشکیل می دهند. این اشکال با توجه به وجه خود نام هایی دارند که معمولاً چند ضلعی هستند. رایج ترین نام ها مکعب، شش وجهی و غیره هستند. اجازه دهید با انواع چندوجهی بیشتر آشنا شویم و برای درک بهتر شکل، چند مثال حل کنیم.

تعریف چند وجهی

چند وجهی یک جامد سه بعدی است که از چند ضلعی تشکیل شده است. دارای وجههای صاف، یالهای مستقیم و رئوس است. به عنوان مثال، مکعب، منشور یا هرم چند وجهی هستند. مخروط ها، کره ها و استوانه ها غیرچند وجهی هستند زیرا اضلاع آنها چند ضلعی نیستند و دارای سطوح منحنی هستند. جمع چندوجهی به چندوجهی نیز معروف است. آنها به عنوان منشور ، اهرام، و جامدات افلاطونی طبقه بندی می شوند . به عنوان مثال، منشور مثلثی، منشور مربع، هرم مستطیلی، هرم مربع و مکعب (جامد افلاطونی) چند وجهی هستند. شکل زیر را مشاهده کنید که انواع مختلف چند وجهی را نشان می دهد.

قطعات یک چند وجهی

ابعاد یک چند وجهی به صورت وجه، لبه و رئوس طبقه بندی می شود.

• وجه: سطح صاف یک چندوجهی را صورت آن می نامند.
• یال: دو وجه در خطی به نام یال به هم می رسند.
• رئوس: نقطه تلاقی دو یال یک راس است.

به شکل زیر توجه کنید که وجه، راس و یالهای یک شکل را نشان می دهد.

انواع چند وجهی

چند وجهی عمدتاً به دو نوع تقسیم می شود - چند وجهی منظم و چند وجهی نامنظم.

چندوجهی منظم

به چندوجهی منتظم جامدات افلاطونی نیز گفته می شود که وجوه آن چند ضلعی منتظم و متجانس با یکدیگر هستند. در یک چندوجهی منظم، تمام زوایای چند وجهی با هم برابرند. پنج چند وجهی منظم وجود دارد. در زیر لیستی از پنج چند وجهی منظم آمده است.

• چهار وجهی: چهار وجهی دارای 4 وجه، 6 یال و 4 راس (گوشه) است. و شکل هر صورت یک مثلث متساوی الاضلاع است.
• مکعب: یک مکعب دارای 6 وجه، 12 یال و 8 رأس است. و شکل هر صورت مربع است.
• هشت وجهی منتظم : یک هشت وجهی منظم دارای 8 وجه، 12 یال و 6 رأس است. و شکل هر صورت یک مثلث متساوی الاضلاع است.
• دوازده وجهی منظم : دوازده وجهی منظم دارای 12 وجه، 30 یال، 20 رأس است. و شکل هر صورت یک پنج ضلعی منظم است.
• Icosahedron منتظم : یک Icosahedron منظم دارای 20 وجه، 30 یال و 12 راس است. و شکل هر وجه یک مثلث متساوی الاضلاع است.

شکل زیر را مشاهده کنید که انواع چندوجهی های منظم را نشان می دهد.

چندوجهی نامنظم

چندوجهی با وجوه چند ضلعی نامنظم که با هم همخوانی ندارند و در آن زوایای چندوجهی برابر نیستند، چندوجهی نامنظم می گویند.

چندوجهی محدب

یک چند وجهی محدب درست مانند یک چندضلعی محدب است. اگر پاره خطی که هر دو نقطه از سطح یک چندوجهی را به هم می‌پیوندد، به طور کامل در داخل چندوجهی قرار گیرد، آن را چندوجهی محدب می‌گویند.

چندوجهی مقعر

یک چند وجهی مقعر کاملاً شبیه چندضلعی مقعر است. اگر پاره خطی که هر دو نقطه از سطح یک چندوجهی را به هم می‌پیوندد به خارج از چند وجهی برود، آن را چندوجهی مقعر می‌گویند.

فرمول چند وجهی

بین تعداد وجه ها، یالها و رئوس در یک چندوجهی رابطه وجود دارد. ما می توانیم این رابطه را به عنوان یک فرمول ریاضی به نام فرمول اویلر نشان دهیم.
فرمول اویلر ⇒ F + V - E = 2، که در آن، F = تعداد وجه ها، V = تعداد راس ها، و E = تعداد یال ها
با استفاده از فرمول اویلر می توانیم به راحتی قسمت گم شده یک چند وجهی را پیدا کنیم. همچنین می‌توانیم بررسی کنیم که آیا یک چند وجهی با تعداد قسمت‌های معین وجود دارد یا خیر. به عنوان مثال، یک مکعب دارای 6 وجه، 8 راس (نقطه گوشه) و 12 یال است. بیایید با استفاده از فرمول اویلر بررسی کنیم که آیا یک مکعب چند وجهی است یا خیر. F = 6، V = 8، E = 12
فرمول اویلر ⇒ F + V - E = 2 که در آن، F = تعداد وجه ها. V = تعداد رئوس. E = تعداد یالها
جایگزینی مقادیر در فرمول: 6 + 8 - 12 = 2 ⇒ 2 = 2. از این رو ثابت شد، مکعب یک چند وجهی است.

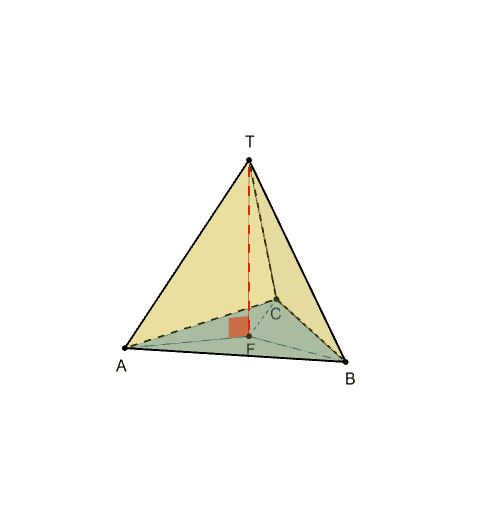
در چهار وجهی منتظم ارتفاع  روی مر کز قاعده فرود می آید

روئوس این چهار وجهی عبارتند از : A,B,C,D

 یالها عبارتند از : a,b.c.d,e.f

وجه ها عبارتند از :ABC,ABD,ADC,BDC

مساحت آن عبارتست از جمع مساحت وجه ها  

ABC+ABD+ADC+BDC=S

محیط آن برابر جمع طول یالها 

P=a+b+c+d+e+f

دایره های مماس خارجی با مراکز در نقاط و شعاع های طول و ، به ترتیب. خطی مماس بیرونی بر هر دو دایره پرتو را در نقطه قطع می کند . چیست ؟

راه حل

اجازه دهید و نقاط مماس بر روی دایره و با خط . . همچنین، اجازه دهید . همانطور که و زوایای قائمه هستند (شعاع عمود بر یک خط مماس در نقطه مماس است) و هر دو مثلث مشترک ، . از این می توانیم نسبتی را بدست آوریم.

مثالها

مثال 1 

مثال 1

داده می شود: ضلع a = 20 ، ضلع c = 24 ، و زاویه γ = 40 درجه . زاویه α مورد نظر است.

با استفاده از قانون سینوس ها نتیجه می گیریم که

توجه داشته باشید که  α = 147.61 درجه حذف می شود زیرا لزوما α + β + γ > 180 درجه را می دهد .

مثال 2 

مثال 2

اگر طول دو ضلع مثلث a و b برابر با x باشد ، ضلع سوم دارای طول c است و زوایای مقابل ضلع های a ، b و c به ترتیب α ، β و γ هستند.