دل نوشته ها ی نقش و آموزش ریاضی  

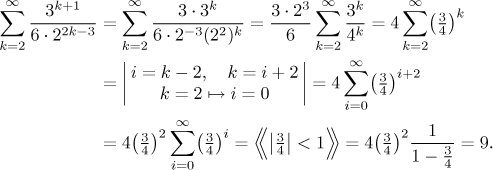
قانون Quotient:

هنگامی که یک تابع از دو عملکرد است یا می توان آنرا به عنوان چنین ذاتی تجزیه کرد ، آنگاه قضیه زیر به ما اجازه می دهد تا مشتق آن را بیابیم:

اگر y = f ( x ) / g ( x ) ،

راه دیگر برای نوشتن این مقاله ، با استفاده از نماد Leibniz است

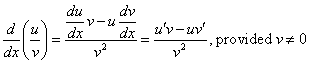
توجه كنيد كه مشتق يك كاركرد فقط توابع مشتقات آنها نيست. این مشتق تا حدودی پیچیده تر است. به این معنا که،

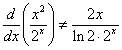
در عوض ، ما داریم

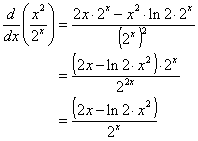
مثال ها:

1. یک عملکرد منطقی از چند جمله ای:

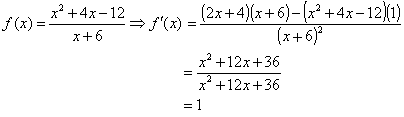
شما باید تأیید کنید که این نتیجه ای است که ما می توانیم به دست بیاوریم که ابتدا عملکرد منطقی را ساده کرده بودیم ، سپس مشتق را می گرفتیم.

2. عملکرد منطقی دیگری که نمی توان جبری را ساده کرد:

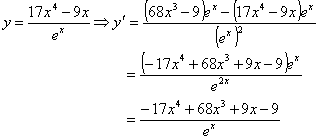
3. نمونه ای از توابع عددی تعریف شده. بگذارید f (2) = 1، f '(2) = -1 ، g (2) = -3 و g' (2) = 4. مشتقات( f ( x ) / g ( x  را در x = 2 پیدا کنید. 

راه حل: براساس قانون quent ، مشتق محصول f و g در x = 2 است

مشتقات توابع نمایی.  

از تعریف مشتق می توان نتیجه گرفت

مثال ها:

1. مشتق 2 x .

2. مشتق 5 (4.6) x .

3. مشتق (ln3) x .

4- مشتق e x .

این نتیجه نهایی نتیجه این واقعیت است که ln e = 1.

ابزارک تصویر

• خانه

• کلاس 11

• ریاضی

• فصل 13 - محدودیت ها و مشتقات

صفحه شماره 301:

سوال 1:

حد مجاز را ارزیابی کنید:

پاسخ:

سوال 2:

حد مجاز را ارزیابی کنید:

پاسخ:

سؤال 3:

حد مجاز را ارزیابی کنید:

پاسخ:

سؤال 4:

حد مجاز را ارزیابی کنید:

پاسخ:

سوال 5:

حد مجاز را ارزیابی کنید:

پاسخ:

سوال 6:

حد مجاز را ارزیابی کنید:

پاسخ:

قرار دادن X + 1 = Y به طوری که Y → 1 به عنوان X → 0.

سؤال 7:

حد مجاز را ارزیابی کنید:

پاسخ:

در x = 2 ، مقدار عملکرد منطقی داده شده شکل را می گیرد .

سؤال 8:

حد مجاز را ارزیابی کنید:

پاسخ:

در x = 2 ، مقدار عملکرد منطقی داده شده شکل را می گیرد .

سؤال 9:

حد مجاز را ارزیابی کنید:

پاسخ:

سؤال 10:

حد مجاز را ارزیابی کنید: 

پاسخ:

در z = 1 مقدار تابع داده شده شکل می گیرد .

به طوری که z → 1 را به عنوان x → 1 قرار دهید.

سؤال 11:

حد مجاز را ارزیابی کنید:

پاسخ:

سؤال 12:

حد مجاز را ارزیابی کنید:

پاسخ:

در x = –2 مقدار تابع داده شده شکل می گیرد .

سؤال 13:

حد مجاز را ارزیابی کنید:

پاسخ:

در x = 0 مقدار تابع داده شده شکل می گیرد .

سؤال 14:

حد مجاز را ارزیابی کنید:

پاسخ:

در x = 0 مقدار تابع داده شده شکل می گیرد .

صفحه شماره 302:

سؤال 15:

حد مجاز را ارزیابی کنید:

پاسخ:

دیده می شود که x → π ⇒ (π - x ) → 0

سؤال 16:

حد مجاز را ارزیابی کنید: 

پاسخ:

سؤال 17:

حد مجاز را ارزیابی کنید:

پاسخ:

در x = 0 مقدار تابع داده شده شکل می گیرد .

اکنون،

سؤال 18:

حد مجاز را ارزیابی کنید:

پاسخ:

در x = 0 مقدار تابع داده شده شکل می گیرد .

اکنون،

سؤال 19:

حد مجاز را ارزیابی کنید:

پاسخ:

سؤال 20:

حد مجاز را ارزیابی کنید:

پاسخ:

در x = 0 مقدار تابع داده شده شکل می گیرد .

اکنون،

سؤال 21:

حد مجاز را ارزیابی کنید:

پاسخ:

در x = 0 مقدار تابع داده شده شکل می گیرد .

اکنون،

سؤال 22:

پاسخ:

در ، مقدار تابع داده شده شکل می گیرد .

اکنون ، اینگونه قرار دهید .

سؤال 23:

یافتن F ( X ) و F ( X )، که در آن F ( X ) =

پاسخ:

تابع داده شده است

f ( x ) =

سؤال 24:

یافتن F ( X )، که در آن F ( X ) =

پاسخ:

تابع داده شده است

سؤال 25:

f ( x ) را ارزیابی کنید ، جایی که f ( x ) =

پاسخ:

تابع داده شده است

f ( x ) =

سؤال 26:

یافتن F ( X )، که در آن F ( X ) =

پاسخ:

تابع داده شده است

سؤال 27:

یافتن F ( X )، که در آن F ( X ) =

پاسخ:

تابع داده شده f ( x ) = است .

سؤال 28:

فرض کنید f ( x ) = و اگر f ( x ) = f (1) مقادیر ممکن از a و b چیست؟

پاسخ:

تابع داده شده است

بنابراین ، مقادیر ممکن مربوطه از a و b 0 و 4 است.

صفحه شماره 303:

سؤال 29:

اجازه دهید شماره های واقعی ثابت باشند و یک تابع را تعریف کنند

چه F ( X )؟ برای برخی محاسبه f ( x ).

پاسخ:

تابع داده شده است .

سؤال 30:

اگر f ( x ) = .

برای چه ارزش (ها) از یک می کند F ( X ) وجود دارد؟

پاسخ:

تابع داده شده است

وقتی یک <0 ،

وقتی a > 0

بنابراین، برای همه وجود دارد ≠ 0.

سؤال 31:

اگر عملکرد f ( x ) راضی است ، ارزیابی کنید .

پاسخ:

سؤال 32:

اگر . برای چه اعداد صحیح متر و N می کند و وجود دارد؟

پاسخ:

تابع داده شده است

بنابراین ، اگر m = n وجود داشته باشد .

بنابراین ، برای هر مقدار جدایی ناپذیر از m و n وجود دارد .