۱۳۹۹/۱۰/۱۳ - - علی رضا نقش نیلچی -
 یک تابع با ارزش بردار است ، ثابت کنید که
یک تابع با ارزش بردار است ، ثابت کنید که  در باز بودن فاصله قابل تغییر است
در باز بودن فاصله قابل تغییر است  اگر و فقط اگر برای تمام
اگر و فقط اگر برای تمام  داشته های ما باشد
داشته های ما باشد
![ارائه شده توسط QuickLaTeX.com \ [F '(t) = \ lim_ {h \ to 0} \ frac {1} {h} (F (t + h) - F (t)). \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-df548eb1de8812336732ffb2ef1022fa_l3.svg)
اثبات اول ، فرض  در قابل تغییر است
در قابل تغییر است  . سپس ، با تعریف تفاوت برای توابع ارزش بردار ما
. سپس ، با تعریف تفاوت برای توابع ارزش بردار ما
![ارائه شده توسط QuickLaTeX.com \ [F '(t) & = (f_1' (t) ، \ ldots ، f_n '(t)) \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-63d25dd44b13e30758c467f6bbb9ad37_l3.svg)
و هر یک از آنها  وجود دارد. بنابراین با تعریف معمول مشتق که داریم
وجود دارد. بنابراین با تعریف معمول مشتق که داریم
![ارائه شده توسط QuickLaTeX.com \ start {align *} F '(t) & = \ left (\ lim_ {h \ to 0} \ frac {f_1 (t + h) - f_1 (t)} {h}، \ ldots، \ lim_ {h \ به 0} \ frac {f_n (t + h) - f_n (t)} {h} \ راست) \\ [9pt] & = \ lim_ {h \ به 0} \ frac {1} {h} \ چپ ((f_1 (t + h) ، \ ldots ، f_n (t + h)) - (f_1 (t) ، \ ldots ، f_n (t)) \ راست) \\ [9pt] & = \ lim_ {h \ به 0} \ frac {1} {h} (F (t + h) - F (t)). \ end {align *}](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-bdd2cc552bec48ffcb811e50be8ba214_l3.svg)
برعکس ، فرض کنید که
![ارائه شده توسط QuickLaTeX.com \ [F '(t) = \ lim_ {h \ to 0} \ frac {1} {h} (F (t + h) - F (t)). \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-df548eb1de8812336732ffb2ef1022fa_l3.svg)
سپس ، حد
![ارائه شده توسط QuickLaTeX.com \ [\ lim_ {h \ to 0} \ frac {1} {h} (f_i (t + h) - f_i (t)) \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-7a02ae7f21c460a7613c647608d031ba_l3.svg)
برای هر یک وجود دارد  . بنابراین ،
. بنابراین ،  برای هر یک وجود دارد
برای هر یک وجود دارد  . بنابراین ،
. بنابراین ،  وجود دارد
وجود دارد
ثابت کنیم که
![ارائه شده توسط QuickLaTeX.com \ [\ lim_ {t \ to p} F (t) = A \ iff \ lim_ {t \ to p} \ lVert F (t) - A \ rVert = 0. \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-6c88b9f9820f629a3fc8ac1227090eaa_l3.svg)
اثبات اجازه دهید
![ارائه شده توسط QuickLaTeX.com \ [F (t) = (f_1 (t) ، \ ldots ، f_n (t)) ، \ qquad \ text {و} \ qquad A = (a_1 ، \ ldots ، a_n). \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-deffe9c080219d3c1ebad36d01fa5d8e_l3.svg)
سپس،

این اگر و فقط در صورت وجود دارد
![ارائه شده توسط QuickLaTeX.com \ [\ lim_ {t \ to p} f_i (t) = a_i \ qquad \ text {for} i = 1، \ ldots، n. \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-029489507da61e2d9ba32df957d7a75f_l3.svg)
از حد معمول این درست است و فقط اگر
![ارائه شده توسط QuickLaTeX.com \ [\ lim_ {t \ to p} | f_i (t) - a_i | = 0 \ qquad \ text {for} i = 1، \ ldots، n. \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-10c080d42671636f8de6284e9c78d836_l3.svg)
این در صورتی است که فقط اگر باشد

بگذارید  ضرب سه گانه اسکالر باشد . ثابت کنیم که .
ضرب سه گانه اسکالر باشد . ثابت کنیم که .
اثبات ما محاسبه می کنیم ،
بدون نظر
اجازه دهید  . محاسبه
. محاسبه  از نظر
از نظر  و
و  .
.
با استفاده از قانون ضرب برای ضرب متقابل ما محاسبه می کنیم ،

از آنجا  که یک بردار که با خودش تلاقی می کند 0 است.
که یک بردار که با خودش تلاقی می کند 0 است.
اجازه بدهید  می شود غیر صفر بردار و
می شود غیر صفر بردار و
![ارائه شده توسط QuickLaTeX.com \ [F (t) = e ^ {2t} A + e ^ {- 2t} B. \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-e6d2762f87fea4b6a4428667d0b775c9_l3.svg)
ثابت کنید که همان جهت را دارد  .
.
اثبات نشان می دهد که  و دارای جهت یکسان باید نشان دهیم که وجود دارد که ثابت وجود دارد
و دارای جهت یکسان باید نشان دهیم که وجود دارد که ثابت وجود دارد  به طوری که . بنابراین ، ما محاسبه می کنیم ،
به طوری که . بنابراین ، ما محاسبه می کنیم ،
بگذارید  یک بردار غیر صفر باشد و
یک بردار غیر صفر باشد و  یک تابع با بردار با ارزش
یک تابع با بردار با ارزش  برای همه داشته باشد
برای همه داشته باشد  ، به گونه ای که زاویه بین
، به گونه ای که زاویه بین  و
و  ثابت باشد. ثابت کنید و
ثابت باشد. ثابت کنید و  متعامد هستند.
متعامد هستند.
اثبات از آنجا که  ما
ما  برای برخی از ثابت است
برای برخی از ثابت است  . از آنجا که زاویه بین
. از آنجا که زاویه بین  و
و  ثابت است ، داریم
ثابت است ، داریم
![ارائه شده توسط QuickLaTeX.com \ [\ frac {F '(t) \ cdot B} {\ lVert F' (t) \ rVert \ lVert B \ rVert} = d \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-17f3850d87eab88807991fbf2a7ab9f7_l3.svg)
برای برخی ثابت است  . بنابراین ،
. بنابراین ،  ثابت است. از این رو ،
ثابت است. از این رو ،  ثابت است ، می گویند
ثابت است ، می گویند  . بنابراین ، ما داریم
. بنابراین ، ما داریم
2 نظر
بگذار  و بگذار
و بگذار
![ارائه شده توسط QuickLaTeX.com \ [B = \ int_0 ^ 1 (te ^ {2t} \ mathbf {i} + t \ cosh (2t) \ mathbf {j} + 2te ^ {2t} \ mathbf {k}) \، dt. \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-6b95026f728b6d651cdfa811dbee138c_l3.svg)
ضرب نقطه را محاسبه کنید  .
.
ابتدا ، انتگرال را با ارزش ارزیابی می کنیم ،
![ارائه شده توسط QuickLaTeX.com \ start {align *} B & = \ int_0 ^ 1 (te ^ {2t} \ mathbf {i} + t \ cosh (2t) \ mathbf {j} + 2te ^ {2t} \ mathbf {k}) \، dt \\ [9pt] & = \ left (\ frac {1} {4} + \ frac {1} {4} e ^ 2، \ frac {1} {4} + \ frac {1} {2} \ sinh 2 - \ frac {1} {4} \ cosh 2، \ frac {1} {2} - \ frac {3} {2} e ^ {- 2} \ right). \ end {align *}](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-745af83def453ef11f8ee1d8e05077fb_l3.svg)
بنابراین ، ضرب نقطه است
![ارائه شده توسط QuickLaTeX.com \ start {align *} A \ cdot B & = \ frac {1} {2} + \ frac {1} {2} e ^ 2 - 1 - 2 \ sinh 2 + \ cosh 2 + \ frac {1} { 2} - \ frac {3} {2} e ^ {- 2} \\ [9pt] & = \ frac {1} {2} e ^ 2 - e ^ 2 + e ^ {- 2} + \ frac { 1} {2} e ^ 2 + \ frac {1} {2} e ^ {- 2} - \ frac {3} {2} e ^ {- 2} \\ [9pt] & = 0. \ end { تراز کردن *}](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-fe52db23d13ef27dad45793e791a3f4c_l3.svg)
محاسبه بردار با ارزش انتگرال
![ارائه شده توسط QuickLaTeX.com \ [\ int_0 ^ 1 (te ^ t \ mathbf {i} + t ^ 2 e ^ t \ mathbf {j} + te ^ {- t} \ mathbf {k}) \، dt. \]](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-fdd5a25497459cf4f6fa8119f9eded4d_l3.svg)
ما محاسبه می کنیم
![ارائه شده توسط QuickLaTeX.com \ start {align *} \ int_0 ^ 1 (te ^ t \ mathbf {i} + t ^ 2 e ^ t \ mathbf {j} + te ^ {- t} \ mathbf {k}) \، dt & = \ سمت چپ (\ int_0 ^ 1 te ^ t \، dt ، \ int_0 ^ 1 t ^ 2 e ^ t \، dt، \ int_0 ^ 1 te ^ {- t} \، dt \ right) \\ [9pt] & = \ چپ (1 ، e-2 ، 1 - \ frac {2} {e} \ راست). \ end {align *}](http://www.stumblingrobot.com/wp-content/ql-cache/quicklatex.com-fddeb264bd18b07f8444df75f76442e7_l3.svg)

![]()
![]()
![]()
![]()
![]()
![]()

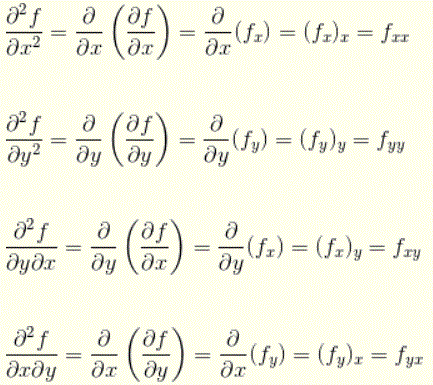





 (
( (
(












![{\displaystyle \sum _{m=1}^{n}m^{3}=\left[{\frac {n(n+1)}{2}}\right]^{2}={\frac {n^{4}}{4}}+{\frac {n^{3}}{2}}+{\frac {n^{2}}{4}}=\left(\sum _{m=1}^{n}m\right)^{2}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b401073f6581dbeae3739e0167704d5749a5917)



 -اُم، و
-اُم، و  عددی منفی است.
عددی منفی است.






 که
که  و
و 

















 در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.
در این وبلاگ شما با ریاضی در سطوح مختلف آشنا خواهید شد.